A Función En matemáticas hay una relación especial entre el conjunto de valores de entrada y el conjunto de valores de salida. En Función, cada valor de entrada proporciona un valor de salida particular. Representamos una función en matemáticas como, y = f(x) donde X es el valor de entrada y para cada X obtenemos un valor de salida como y.

En este artículo, aprenderemos sobre, funciones en matemáticas, sus diversos tipos, ejemplos y otros en detalle.

Tabla de contenidos

• ¿Qué es una función en matemáticas?
• Definición de función en matemáticas
• Ejemplos de funciones
• Condición para una función
• Representación de funciones en matemáticas
• Identificación de función
• Tipos de función
• ¿Qué es una función en álgebra?
• Dominio y rango de una función
• Composición de funciones
• Álgebra de funciones
• ¿Qué es una función en una gráfica?
• Funciones gráficas
• Funciones comunes
• Aplicaciones de funciones
• Ejemplos de función
• Problemas de práctica sobre qué es una función

¿Qué es una función en matemáticas?

Una función en matemáticas es una relación entre los valores de entrada (dominio) y los valores de salida (rango) de los conjuntos dados, de modo que no haya dos variables de los conjuntos de dominio que estén vinculadas a la misma variable en el conjunto de rango. Un ejemplo simple de una función en matemáticas es f(x) = 2x, que se define en R→R, aquí cualquier variable en el dominio está relacionada con una sola variable en el rango.

Una función en matemáticas tiene un dominio, un codominio y un rango. El dominio es el conjunto de todos los valores posibles de x y el rango de la función es el conjunto de todos los valores de salida de y. El rango es el subconjunto del codominio de una función. También podemos decir que una función en matemáticas es una relación con una salida única y no hay dos valores de entrada que tengan una salida similar en una función, como es el caso de la relación.

Definición de función en matemáticas

Una función es una relación o método especial que conecta cada miembro del conjunto A con un miembro único del conjunto B a través de una relación definida. El conjunto A se llama dominio y el conjunto B se llama codominio de la función. Una función en matemáticas del conjunto A al conjunto B se define como,

f = ∀ una ∈ A, b ∈ B

Toda función es una relación pero toda relación no es una función. El criterio para que cualquier relación se considere una función es que en función cada elemento del conjunto A tiene solo una imagen en el conjunto B, mientras que en relación un elemento del conjunto A puede tener más de una imagen en el conjunto B.

Definimos funciones en matemáticas desde el conjunto A no vacío hasta el conjunto B no vacío tal que,

(a, b) ∈ f, entonces f(a) = b

donde llamamos b como la imagen de a definido bajo la relación F .

Cada elemento 'a' del conjunto A tiene una imagen única ' b ' en el conjunto B entonces es una función.

Ejemplos de funciones

Una función en matemáticas f se define como, y = f(x) donde X es el valor de entrada, y para cada valor de entrada de x, obtenemos un valor único de y. Varios ejemplos de funciones matemáticas definidas en R → R son,

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3, etc.

Condición para una función

Para dos conjuntos cualesquiera A y B no vacíos, una función f: A→B denota que F es una función de A a B, donde A es un dominio y B es un codominio.

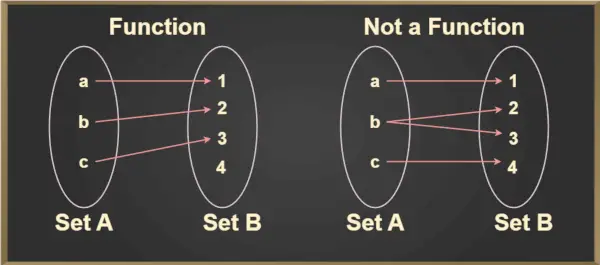
Para cualquier elemento, a ∈ A, un elemento único, b ∈ B, existe tal que (a,b) ∈ f. El elemento único b que está relacionado con a se denota por f(a) y se lee como f de a. Esto se puede entender mejor en la siguiente imagen:

Prueba de línea vertical

La prueba de la línea vertical se utiliza para determinar si una curva es una función o no. Si alguna curva corta una línea vertical en más de un punto, entonces la curva no es una función.

Representación de funciones en matemáticas

Representamos una función en matemáticas como,

y = f(x) = x + 3

Aquí, el conjunto de valores de x es el dominio de la función y el conjunto de valores de salida de y es el codominio de la función. Aquí, la función se define para todos los números reales, ya que proporciona un valor único para cada x, pero no siempre es posible obtener el resultado para cada valor de x, en tal caso definimos la función en dos partes, esto puede entenderse como

• f(x) = 1/(x – 2), donde x ≠ 2
• f(x) = x²donde x ∈ {R}

Podemos definir una función en matemáticas como una máquina que toma alguna entrada y da una salida única. La función f(x) = x²se define a continuación como,

Podemos representar una función en matemáticas mediante los tres métodos como,

cual es el tamaño de mi monitor

• Conjunto de pares ordenados
• Formulario de tabla
• Forma gráfica

Por ejemplo, si representamos una función como, f(x) = x³

Otra forma de representar la misma función es como conjunto de pares ordenados como,

f = {(1,1), (2,8), (3,27)}

En el conjunto mencionado anteriormente, el dominio de la función es D = {1, 2, 3} y el rango de la función es R = {1, 8, 27}

Identificación de función

La función se clasifica como un tipo especial de relación en matemáticas. Existen las siguientes reglas que se pueden utilizar para identificar una función:

• Una relación en la que cada entrada asignada a una salida única es una Función. Esto se llama función uno a uno.
• Una relación en la que dos entradas (preimagen) asignadas a una única salida también es una función. Esta es una función de muchos a uno.
• Una relación en la que una entrada se asigna a dos salidas diferentes no es una función.
• Una relación en la que muchas entradas se asignan a muchas salidas sin seguir ninguna regla específica no es una función.

Tipos de función

Diferente Tipos de funciones Se utilizan para resolver varios tipos de problemas matemáticos, especialmente relacionados con curvas y ecuaciones. Hay tres tipos principales de funciones en matemáticas que se basan en el mapeo de elementos del conjunto A al conjunto B.

Función inyectiva o función uno a uno

La función en la que cada elemento del dominio tiene una imagen distinta en el codominio se llama inyectivo o Función uno a uno .

f: Se dice que A → B es uno a uno o inyectivo si las imágenes de distintos elementos de A bajo f son distintas, es decir,

fa ₁ ) = segundo ₁ , f(a ₂ ) = segundo ₂

donde un₁, a₂∈ A y b₁, b₂∈B

Funciones sobreyectivas o sobre función

La función sobreyectiva es la función en la que cada elemento del codominio tiene una preimagen en el dominio. También es llamado Sobre la función lo que significa que cada elemento del codominio está asociado con cada elemento del dominio. Ningún elemento del codominio debe tener una relación vacía. El número de elementos del codominio y del rango es el mismo.

f: Se dice que A → B es sobre, si cada elemento de B es la imagen de algún elemento de A bajo f, es decir, para cada b ϵ B, existe un elemento 'a' en A tal que f(a) = b.

Función biyectiva

Si una función tiene propiedades tanto de Inyectiva (Uno a Uno) como de Suryectiva (Sobre la función), entonces la función se llama Función biyectiva . En la función biyectiva, cada elemento del dominio está relacionado con cada elemento del codominio y también existe una relación uno a uno. Esto implica que el número de elementos del codominio y el rango son los mismos y ningún elemento ni en el dominio ni en el codominio tiene una relación vacía.

Según los valores de salida, las funciones se clasifican como funciones pares e impares. Echemos un vistazo a ellos

Funciones impares

La función impar es un tipo de función que exhibe simetría con respecto al origen. Específicamente, si f(x) es una función impar, muestra que f(-x) = -f(x)

Función uniforme

La función par es un tipo de función que exhibe simetría con respecto al eje y. Específicamente, si f(x) es una función par, muestra que f(-x) = f(x)

java ordenando una lista

¿Qué es una función en álgebra?

Una función en álgebra es una ecuación para la cual cualquier x que se pueda poner en la ecuación producirá exactamente una salida como y fuera de la ecuación. Se representa como y = f(x), donde x es una variable independiente e y es una variable dependiente.

Por ejemplo:

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Dominio y rango de una función

Dominio y rango de una función son valores de entrada y salida de una función respectivamente. Por ejemplo, digamos que tenemos una función dada como f(x) = x². Aquí, podemos tomar todos los números reales como valor de entrada de x y la salida siempre será un número real positivo. Por lo tanto, su dominio está formado por todos los números reales representados como R, mientras que su rango es el conjunto de números reales positivos representados como R.⁺

Composición de funciones

Si f: A → B y g: B→ C son dos funciones. Entonces la composición de f y g se denota como f(g) y se define como la función niebla = f(g(x)) para x ∈ A.

Tomemos dos funciones f(x) = x + 3 y g(x) = 2x²

niebla = f(g(x))

⇒ niebla = f(2x²)

⇒ diente = 2x²+ 3

Aprende más, Composición de la función

Álgebra de funciones

El álgebra de funciones implica las operaciones algebraicas realizadas entre dos funciones. A continuación se menciona la operación algebraica para dos funciones f(x) y g(x) definidas sobre el valor real de x:

cambiar el nombre de la carpeta de Linux

• (f + g) (x) = f(x) + g(x)
• (f – gramo) (x) = f(x) – gramo(x)
• (f.g) (x) = f(x).g(x)
• (k·f(x)) = k (f(x)); {Porque k es un número real}
• (f/g)(x) = f(x) /g(x); {Para g(x) ≠ 0}

¿Qué es una función en una gráfica?

Una función se puede representar fácilmente en una gráfica. Cualquier función en el gráfico representa una curva (incluida la línea recta) en el plano xy asignada para sus valores de entrada y salida correspondientes.

Para trazar una función en un primero, encuentre algunos puntos que se encuentren en la función y luego una estos puntos de acuerdo con el lugar de la función. Por ejemplo, para graficar la función (línea recta) f(x) = y = 5x – 2 necesitamos algún punto en la gráfica. Para encontrar el punto en la gráfica, primero tomamos los valores aleatorios de x y luego encontramos sus valores correspondientes de y, como,

f(x) = y = 5x- 2

si x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

si x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

si x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Ahora uniendo estos puntos podemos obtener la gráfica de la función y = 5x – 2

Funciones gráficas

Conocer los valores de x permite representar una función f(x) en una gráfica. Como y = f(x), podemos encontrar el valor asociado para y comenzando con los valores de x. Como resultado, podemos trazar una gráfica en un plano de coordenadas usando los valores de x e y. Considere el siguiente escenario:

Assume y = x + 3

Cuando x = 0, y = 3

Similarmente,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Como resultado, podemos trazar la gráfica de la función x + 3 usando estos valores.

Funciones comunes

A continuación se analizan algunas funciones comunes que se usan comúnmente en matemáticas:

Función real

función real en matemáticas se refiere a una función cuyo dominio y rango son subconjuntos de los números reales (denotados como ℝ). En términos más simples, una función real es una regla o relación matemática que asigna un valor de número real a cada entrada de número real.

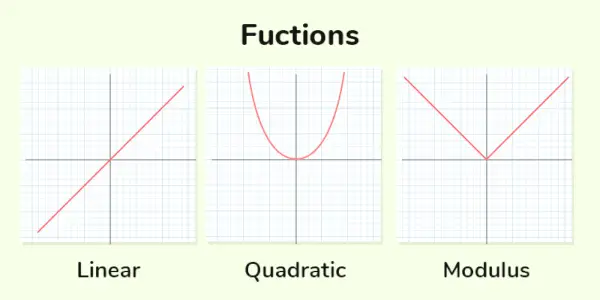
Funciones reales

Función polinómica

La función en la que los exponentes de variables algebraicas son números enteros no negativos se llama Función polinómica . Si la potencia de la variable es 1 se llama función lineal, si la potencia es 2 se llama función cuadrática y si la potencia es 3 se llama función cúbica. Algunos ejemplos de funciones polinómicas se mencionan a continuación:

• y = x²
• y = 2x + 3
• y = 3x³

La función polinómica se puede clasificar además en los siguientes tipos:

Función lineal : Las funciones lineales son aquellas en las que la potencia máxima de la variable es 1. La forma general de Función lineal es y = mx + c

Función cuadrática : Las funciones cuadráticas son aquellas en las que la potencia máxima de la variable es 2. Forma general de función cuadrática es, hacha ² + bx + c = 0

Función cúbica : Función cúbica son aquellos en los que la potencia máxima de la variable es 3. La forma general de la función cúbica se da como hacha ³ + bx ² + cx + d = 0

Función inversa

Función inversa es la función que contiene la inversa de otra función. Digamos que tenemos una función y = f(x) entonces su función inversa será x = f^-1(y). En y = f(x), el dominio es x y el rango es y mientras que en el caso de x = f^-1(y), el dominio es y y el rango es x. Así podemos decir que el dominio de la función original es el rango de su función inversa y el rango de la función original es el dominio de la función original. Algunos ejemplos de funciones inversas son,

• y = tan^-1(X)
• y = x^-1

Función de área

La función de área generalmente se refiere a una función matemática que calcula el área de una forma o región geométrica. La función de área toma uno o más parámetros como entrada y devuelve el área de la forma correspondiente. Algunas de las funciones del área se analizan a continuación:

Función del área del círculo : Área del círculo (A) es una función de su radio (r) tal que,

A = πr ²

Área de la función triangular : Área del Triángulo (A) es una función de su base (b) y altura (h) tal que,

A = (bh)/2

Funcion exponencial

Funcion exponencial es el que se representa como f(x) = e^X. A menudo se utiliza para mostrar un rápido crecimiento o decadencia.

Función logarítmica

función logarítmica es una función matemática que representa la operación inversa de la exponenciación. Se representa como f(x) = log x.

Función de techo

Función de techo , denotado como ⌈x⌉, redondea un número real x al entero más cercano que sea mayor o igual a x. En otras palabras, encuentra el valor entero más pequeño que sea mayor o igual a x.

Función de piso

La función suelo, denotada como ⌊x⌋, redondea un número real x al número entero más cercano que sea menor o igual a x. En otras palabras, encuentra el valor entero más grande que sea menor o igual a x.

Función de módulo

Función de módulo , también conocida como función de valor absoluto, devuelve la magnitud o el tamaño de un número real sin tener en cuenta su signo. La función de módulo se denota como ∣x∣, donde x es el valor de entrada.

Función de signo

función de signo , también conocida como función de signo o función signum, es una función matemática que devuelve el signo de un número real. Indica si el número es positivo, negativo o cero.

llamar a una función js desde html

Funciones trigonométricas

Funciones trigonométricas son funciones matemáticas que relacionan los ángulos de un triángulo rectángulo con las longitudes de sus lados. Las seis funciones trigonométricas principales son seno (sin), coseno (cos), tangente (tan), cosecante (cosec), secante (sec) y cotangente (cot).

Funciones complejas

Cualquier función en la que la variable de entrada sea una función compleja se denomina función compleja. Un número complejo es un número que se puede trazar en el plano complejo. en un Número complejo tenemos un número real y un número imaginario. Un número complejo (z) se representa como z = x + iy y una función compleja se representa como f(z) = P(x, y) + iQ(x, y)

Aplicaciones de funciones

Cuando decimos que una cantidad variable y es función de una cantidad variable x, indicamos que y depende de x y que el valor de y está determinado por el valor de x. Esta dependencia se puede expresar de la siguiente manera: f = y (x).

• El radio de un círculo se puede utilizar para calcular el área de un círculo. El radio r afecta al área A. Declaramos que A es función de r en el lenguaje matemático de funciones. Podemos escribir A = f(r) =π×r²
• El volumen V de una esfera es función de su radio. V = f(r) = 4/3×r³denota la dependencia de V de r.
• La fuerza es función de la aceleración de un cuerpo de masa fija m. F = g(a) = m×a.

La gente también leyó:

• Relación y función
  
• Dominio y rango de funciones trigonométricas
• Rango de una función
• Función hiperbólica

Ejemplos de función

Ejemplo 1: Para dos funciones, f y g se definen como, f(x) = x ² y g(x) = ln(2x). Encuentra la función compuesta (gof )( x )

Solución:

Dado:

• f(x) = x²
• g(x) = ln(2x)

(gof)(x) = g(f(x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Por lo tanto, (gof)(x) = 2 ln(√2x)

Ejemplo 2: Encuentre la salida de la función g(t)= 6t ² + 5 en

• (yo) t = 0
• (ii) t = 2

Solución:

función dada,

diferencia entre un león y un tigre

gramo(t)= 6t²+ 5t

• (yo) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Ejemplo 3: El largo de un rectángulo es cinco veces su ancho, expresa el área del rectángulo en función de su largo.

Solución:

Sea la longitud del rectángulo l y el ancho del rectángulo b

Ahora,

• b = l/5

Área del Rectángulo(A) = l × l/5 = l²/5

Por tanto, el área del rectángulo en función de su longitud es,

A(l) = l ² /5

Problemas de práctica sobre qué es una función

1. Dada la función f(x)=3x+5

• Encuentre f(2)
• Encuentre f(-1)
• Determine el dominio y rango de la función.

2. Dada la función g(x)=x ² – 4x + 3

• Encuentra las raíces de la función.
• Encuentre g(3) y g(0).
• Determina el vértice de la función.

3. Dadas dos funciones f(x)=x + 2 y h(x)=2x – 3

• Encuentra la función compuesta (f ∘ h) (x)
• Evaluar (f ∘ h)(2)

Resumen: ¿Qué es una función?

Una función en matemáticas es una relación especial entre los valores de entrada (dominio) y los valores de salida (rango) donde cada entrada está asociada con una salida única. Representadas como y = f(x), las funciones tienen características específicas y se pueden visualizar mediante pares ordenados, tablas o gráficos. Son esenciales en varios problemas matemáticos y vienen en diferentes tipos, incluidos inyectivos (uno a uno), sobreyectivos (sobre) y biyectivos (ambos). Las funciones se pueden probar utilizando la prueba de la línea vertical y se clasifican en funciones polinomiales, inversas, exponenciales, logarítmicas y trigonométricas. Comprender las funciones implica reconocer su dominio, rango y las reglas que las definen. Los ejemplos incluyen funciones lineales simples como y = 2x + 1 y composiciones complejas de funciones. Las funciones desempeñan un papel crucial en álgebra, geometría y cálculo, ayudando en la representación y análisis de relaciones matemáticas y fenómenos del mundo real.

Preguntas frecuentes sobre qué es una función

¿Cuál es la definición de función?

Una relación f definida en un conjunto A con otro conjunto B se llama función en matemáticas si cada valor de A tiene un valor único en el conjunto B.

¿Cómo escribir una función en matemáticas?

La función f en matemáticas se representa como f: A → B y se define como, f(x) = x + 2. Aquí, para cada valor único de x, tenemos un valor único de y.

¿Cómo transformar una función?

Podemos transformar fácilmente una función en otras funciones simplemente realizando operaciones algebraicas básicas en la función. Las diferentes transformaciones de la función son reflexión, traslación, rotación, etc.

¿Qué es una función racional?

Una función fraccionaria donde el numerador y el denominador son funciones polinomiales se llama función racional. Algunos ejemplos de la función racional son,

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), etc.

¿Qué es una función lineal?

Una función algebraica en la que cada término de la función es constante o tiene una potencia de uno se llama función lineal. Algunos ejemplos de la función lineal son,

• f(x) = 2x + 3
• gramo(x) = x – 5, etc.

¿Qué son el dominio y el codominio de una función?

Si definimos la función como, y = f(x). Entonces el dominio de x son todos los valores de x para los cuales y resulta en un valor único. Y el codominio de y es el conjunto de todos los valores de y para cada valor de x.

¿Cómo se identifica una función en matemáticas?

Si cualquier valor de entrada (x) del dominio en una relación tiene más de una imagen (y), entonces esta relación nunca podrá ser una función. Entonces, si el valor de x se repite en el par ordenado, entonces nunca es una función.