Los Números Complejos son la continuación natural de los números reales. En la era moderna, los números complejos se utilizan en muchos campos, como el procesamiento de señales digitales, la criptografía y muchos campos relacionados con la informática.

En este artículo, aprenderemos sobre los números imaginarios, los números complejos y su tipo, varias operaciones con números complejos, las propiedades de los números complejos, la aplicación de los números complejos, etc.

Definición de números complejos

Números complejos son los números de la forma (a + i b) dónde a & b son los números reales y i es una unidad imaginaria llamada iota que representa √-1. Por ejemplo, 2 + 3i, es un número complejo en el que 2 es un número real y 3i es un número imaginario. Los números complejos se pueden escribir como a + ib donde a y b son números racionales que se pueden representar en una recta numérica que se extiende hasta infinidad .

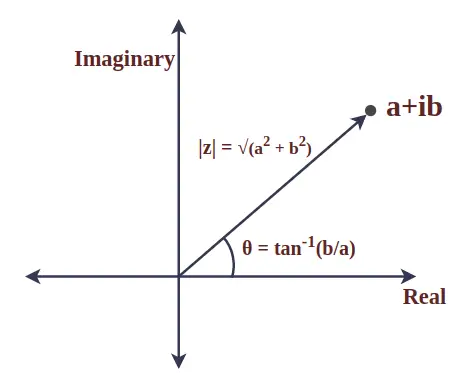
Módulo de número complejo

El módulo del número complejo es el valor absoluto y representa la distancia entre el origen y el punto dado. También se le conoce como magnitud del número complejo. Consideremos un número complejo z = a + ib, entonces el módulo de z se define como:

|z| = √(un ² +b ² )

dónde,

• a es la parte real del número complejo z, y
• b es la parte imaginaria del número complejo z.

Argumento del número complejo

El ángulo entre el vector radio de un número complejo y el eje x positivo se llama argumento de un número complejo. Para un número complejo z = a + ib, matemáticamente viene dado por:

θ = tan ^-1 (licenciado en Letras)

dónde,

• a es la parte real del número complejo z, y
• b es la parte imaginaria del número complejo z.

Poder de i(iota)

La i(iota) se define como la raíz cuadrada de -1. Por tanto, cualquier potencia de i puede expresarse como una multiplicación repetida de i por sí mismo, es decir,

• yo = √(-1)
• i²= -1
• i³= – yo
• i⁴= 1
• i⁵= yo
• i⁶= – 1
• etcétera..

Necesidad de números complejos

En la antigüedad, la gente sólo conocía los números naturales, ya que estos números son de naturaleza más intuitiva, ya que el cerebro humano ya los comprende mediante imágenes de cosas como ovejas y comida. Así, sólo tenemos el conjunto de los números naturales ( norte ) pero en los números naturales, no hay solución para la ecuación x + a = b (a> b) y a, b ∈ N. Por lo tanto, surgió una extensión de los números naturales, es decir, los enteros ( I ).

Ahora, nuevamente en este conjunto de números, no hay solución para la ecuación, ax = b (a ≠ 0) y a, b ∈ I, donde a y b son números enteros. Así, un conjunto de números enteros (I) se extiende a un conjunto de números racionales ( q ).

Nuevamente, en este conjunto de números racionales, no hay solución para la ecuación x²= a (a> 0) y a ∈ Q. Así, q se extiende para incluir números tales que, x²= a(para a> 0) es decir, números irracionales. Este conjunto se llama Números Reales y está representado por R .

Ahora bien, durante mucho tiempo se pensó que no teníamos que ampliar este conjunto de números reales para formar otro conjunto más grande, ya que esta colección de números parece completa. Pero nuevamente surgió un nuevo problema en este conjunto de números, es decir, no existe un número real tal que x²= a (a <0) y a ∈ R. Por lo tanto, el conjunto de números reales se extiende aún más para incluir todos los valores y denomina a este conjunto Números Complejos y está representado por C .

Clasificación de números complejos

Como sabemos, la forma estándar de un número complejo es z = (a + i b) donde a, b ∈ R, i es iota (una unidad imaginaria). Así, dependiendo de los valores de a (llamada parte real) y b (llamada parte imaginaria), los números complejos se clasifican en cuatro tipos:

• Número complejo cero
• Números puramente reales
• Números puramente imaginarios
• Números imaginarios

Conozcamos estos tipos en detalle.

Número complejo cero

Para cualquier número complejo z = a + ib, si a = 0 y b = 0, entonces el número complejo se llama número complejo cero. Por ejemplo, el único ejemplo de esto es 0.

Números puramente reales

Para cualquier número complejo z = a + ib, si a ≠ 0 y b = 0, entonces el número complejo se llama número puramente real, es decir, un número sin parte imaginaria. Todos los números reales son ejemplos de esto tales como 2, 3, 5, 7, etc.

Números puramente imaginarios

Para cualquier número complejo z = a + ib, si a = 0 y b ≠ 0, entonces un número complejo se llama número puramente imaginario, es decir, un número sin parte real. Todos los números sin partes reales son ejemplos de este tipo de número, es decir, -7i, -5i, -i, i, 5i, 7i, etc.

Números imaginarios

Para cualquier número complejo z = a + ib, si a ≠ 0 y b ≠ 0, entonces un número complejo se llama número imaginario . Por ejemplo, (-1 – i), (1 + i), (1 – i), (2 + 3i), etc.

Diferentes formas de números complejos

Hay varias formas de números complejos que son,

• Forma rectangular
• Forma polar
• Forma exponencial

Ahora conozcamos sobre ellos en detalle.

Forma rectangular

Forma rectangular es también llamado Forma estándar y está representado por (a + ib), donde a y b son los números reales.

Por ejemplo: (5 + 5i), (-7i), (-3 – 4i), etc.

Forma polar

Forma polar es la representación de un número complejo donde las coordenadas polares [donde las coordenadas se representan como (r, θ), donde r es la distancia desde el origen y θ es el ángulo entre la línea que une el punto y el origen y el eje x positivo) Se utilizan para representar un número complejo. Cualquier número complejo se representa como r [cos θ + i sen θ].

Por ejemplo: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6], etc.

Forma exponencial

Formas exponenciales de números complejos es la representación de números complejos usando la fórmula de Euler y en esta forma el número complejo se representa por reⁱ, donde r es la distancia de un punto desde el origen y θ es el ángulo entre el eje x positivo y el vector de radio.

Por ejemplo: mi^yo(0), Es^yo(π/2), 5.e^yo(π/6), etc.

Nota: Las tres formas de números complejos analizadas anteriormente son interconvertibles, es decir, se pueden convertir de una forma a otra muy fácilmente.

Operaciones con números complejos

Se pueden realizar las siguientes operaciones con Números Complejos:

• Suma
• Sustracción
• Multiplicación
• División
• Conjugación

Suma de números complejos

Podemos sumar dos números complejos, simplemente sumando sus partes real e imaginaria por separado.

Por ejemplo, (3 + 2i) + (1 + 4i) = 4 + 6i.

Resta de números complejos

Podemos restar dos números complejos, simplemente restando sus partes real e imaginaria por separado.

Por ejemplo, (3 + 2i) – (1 + 4i) = 2 – 2i.

Multiplicación de números complejos

Podemos multiplicar dos números complejos usando la propiedad distributiva y el hecho de que i²= -1.

Por ejemplo, (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

División de números complejos

Podemos dividir un número complejo por otro, simplemente multiplicando tanto el numerador como el denominador por el conjugado complejo del denominador y simplificando aún más la expresión.

subcadena de cadena java

Por ejemplo, (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Conjugación de números complejos

Podemos encontrar fácilmente el conjugado de un número complejo, simplemente cambiando el signo de su parte imaginaria. El conjugado de un número complejo a menudo se indica con una barra encima del número, como z̄.

Por ejemplo, el conjugado de 3 + 2i es 3 – 2i.

Identidades para números complejos

Para dos números complejos cualesquiera z₁yz₂Se pueden dar las siguientes identidades algebraicas:

• (Con ₁ +z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ ×z ₂
• (Con ₁ - Con ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ ×z ₂
• (Con ₁ ) ² - (Con ₂ ) ² = (z ₁ +z ₂ )(Con ₁ - Con ₂ )
• (Con ₁ +z ₂ ) ³ = (z ₁ ) ³ + 3(z) ₁ ) ² Con ₂ +3(z) ₂ ) ² Con ₁ + (z ₂ ) ³
• (Con ₁ - Con ₂ ) ³ = (z ₁ ) ³ – 3(z) ₁ ) ² Con ₂ +3(z) ₂ ) ² Con ₁ - (Con ₂ ) ³

Fórmulas relacionadas con números complejos

Existen algunas fórmulas relacionadas con números complejos, algunas de las cuales son las siguientes:

Fórmula de Euler

La fórmula de Euler muestra la relación entre la potencia imaginaria del exponente y la razón trigonométrica sin y cos y viene dada por:

Es ^ix = cos x + i sin x

La fórmula de De Moivre

La fórmula de De Moivre expresa el n^thpotencia de un número complejo en forma polar y viene dada por:

(cos x + i sin x) ^norte = cos (nx) + i sin (nx)

Plano complejo

El plano en el que se representan de forma única los números complejos se denomina plano complejo, plano de Argand o plano gaussiano.

El plano Complejo tiene dos ejes:

• Eje X o Eje Real
• Eje Y o Eje Imaginario

Eje X o Eje Real

• Todos los números complejos puramente reales están representados de forma única por un punto.
• La parte real Re(z) de todos los números complejos se traza con respecto a ella.
• Por eso el eje X también se llama eje real .

Eje Y o Eje Imaginario

• Todos los números complejos puramente imaginarios están representados de forma única por un punto.
• La parte imaginaria Im(z) de todos los números complejos se traza con respecto a ella.
• Por eso el eje Y también se llama Eje imaginario .

Representación geométrica de números complejos

Como sabemos, cada número complejo (z = a + i b) está representado por un punto único p (a, b) en el plano complejo y cada punto en el plano complejo representa un número complejo único.

Para representar cualquier número complejo z = (a + i b) en el plano complejo, siga estas convenciones:

• La parte real de z (Re(z) = a) se convierte en la coordenada X del punto p

• La parte imaginaria de z (Im(z) = b) se convierte en la coordenada Y del punto p

Y finalmente z (a + i b) ⇒ p (a, b) que es un punto en el plano complejo.

Propiedades de los números complejos

Existen varias propiedades de los números complejos, algunas de las cuales son las siguientes:

• Para cualquier número complejo z = a + ib, si z = 0 entonces a = 0 y b = 0.
• Para 4 números reales a, b, cyd tales que z₁= a + ib y z₂= c + id. si z₁=z₂entonces a = c y b = d.
• La suma de un número complejo con su conjugado da como resultado un número puramente real, es decir, z + z̄ = Número real.

Sea z = a + ib,

z + z̄ = a + uno + a – uno

⇒ z + z̄ = 2a (que es puramente real)

• El producto de un número complejo con sus resultados conjugados también es un número puramente real, es decir, z × z̄ = Número real

Sea z = a + ib, entonces

z × z̄ = (a + uno) × (a – uno)

⇒ z × z̄= a²- i²b²

⇒ z × z̄ = a²+b²(que es puramente real)

• Los números complejos son conmutativo bajo la operación de suma y multiplicación. Consideremos dos números complejos z₁yz₂, y luego

Con ₁ +z ₂ =z ₂ +z ₁

Con ₁ ×z ₂ =z ₂ ×z ₁

• Los números complejos son de asociación con la operación de suma y multiplicación. Consideremos tres números complejos z₁, Con₂y z₃entonces

(Con ₁ +z ₂ ) + z ₃ =z ₁ + (z ₂ +z ₃ )

(Con ₁ ×z ₂ )×z ₃ =z ₁ ×(z) ₂ ×z ₃ )

• Los números complejos mantienen el Propiedad distributiva de la multiplicación sobre la suma también. Consideremos tres números complejos z₁, Con₂y z₃entonces

Con ₁ ×(z) ₂ +z ₃ ) = z ₁ ×z ₂ +z ₁ ×z ₃

Leer más,

• Dividir números complejos
• Barra Z en números complejos

Ejemplos de números complejos

Ejemplo 1: trazar estos números complejos z = 3 + 2i en el plano Complejo.

Solución:

Dado:

Con = 3 + 2 yo

Entonces, el punto es z(3, 2). Ahora trazamos este punto en el siguiente gráfico, aquí en este gráfico el eje x representa la parte real y el eje y representa la parte imaginaria.

Ejemplo 2: trazar estos números complejos z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 yo), z ₄ = (1 – i) en el plano Complejo.

Solución:

Dado:

Con₁= (2 + 2 yo)

Con₂= (-2 + 3 yo)

Con₃= (-1 – 3yo)

Con₄= (1 – yo)

Entonces los puntos son z₁(2, 2), z₂(-2, 3), z₃(-1, -3) y z₄(1, -1). Ahora trazamos estos puntos en el siguiente gráfico, aquí en este gráfico el eje x representa la parte real y el eje y representa la parte imaginaria.

cómo ordenar la lista de matrices en java

Preguntas frecuentes sobre números complejos

Definir números complejos.

Los números de la forma a+ib se llaman números complejos, donde a y b son el número real e i es la unidad imaginaria que representa la raíz cuadrada de -1.

¿Cuál es la diferencia entre un número real y un número complejo?

La diferencia entre números reales y complejos es que solo necesitamos un número para representar cualquier número real, pero necesitamos dos números reales para representar cualquier número complejo.

¿Cuál es la parte real y la parte imaginaria de un número complejo?

En un número complejo a + ib, a es la parte real del número complejo y b se llama parte imaginaria del número complejo.

¿Cuál es el conjugado complejo de un número complejo?

Para un número complejo a + ib, a – ib se llama su conjugado complejo. Los conjugados complejos se pueden encontrar simplemente cambiando el signo de la parte imaginaria.

¿Cuál es el módulo de un número complejo?

La distancia entre el origen y el punto representado por un número complejo en el plano de argando se llama módulo de ese número completo y para z = a + ib, matemáticamente viene dado por:

|z| = √(un ² +b ² )

¿Cuál es el argumento de un número complejo?

El ángulo entre el vector de radio de un número complejo y el eje x positivo se llama argumento de un número complejo y para z = a + ib, matemáticamente viene dado por:

θ = tan ^-1 (licenciado en Letras)

¿Cuál es la forma polar de un número complejo?

Para cualquier número complejo, z = a + ib, la forma polar de este viene dada por:

r [cos θ + i sen θ]

¿Cuál es la fórmula de Euler?

La fórmula de Euler muestra la relación entre la potencia imaginaria del exponente y la razón trigonométrica sin y cos y viene dada por:

Es ^ix = cos x + i sin x