el función coseno o el porque La función en resumen es una de las seis. Funciones trigonométricas fundamental para la trigonometria. El coseno en trigonometría se da como la relación entre la base y la hipotenusa de un triángulo rectángulo. La función coseno se representa como Cos x donde x es el ángulo para el cual se calcula la relación del coseno. En términos de función, podemos decir que x es la entrada o el dominio de la función coseno.
Se utiliza ampliamente en una amplia gama de materias como Física, Geometría e Ingeniería, entre otras, generalmente aprovechando su naturaleza periódica. Por ejemplo, se utiliza para definir la naturaleza ondulatoria de las ondas sonoras, cálculos del flujo eléctrico a través de una superficie plana, etc. En este artículo, aprendemos en detalle qué es la función coseno, la dominio y rango de la función coseno, el período y la gráfica de la función coseno.
Tabla de contenidos
- ¿Qué es la función coseno?
- Cos en el círculo unitario
- Gráfico de función coseno
- Función inversa de coseno
- Función coseno en cálculo
- Identidades de funciones cos
¿Qué es la función coseno?
La función coseno es una función trigonométrica que es básicamente de naturaleza periódica. La función coseno se expresa como cos x donde x es uno de los ángulos agudos de un triángulo rectángulo. La función coseno encuentra la relación entre la base y la hipotenusa para un valor dado de x. La función coseno se abrevia como cos(x) o cos(θ), donde x es el ángulo en radianes y theta θ es el ángulo en grados generalmente. La función coseno se puede definir utilizando un círculo unitario, es decir, un círculo de radio unitario, como veremos más adelante en este artículo. Es de naturaleza periódica y repite sus valores después de cada rotación completa de ángulos. En un plano cartesiano, se le puede denominar componente vectorial de la hipotenusa paralela al eje x.
Definición de función coseno
La función coseno se define en un triángulo rectángulo como la relación entre la longitud del lado adyacente al ángulo en cuestión y la longitud de la hipotenusa. Matemáticamente la función coseno se da como
Cos x = Cos θ = Longitud de la base/Longitud de la hipotenusa = b/h = OB/OA
dónde X es el ángulo en radianes y θ es el ángulo equivalente en grados.
Dominio y rango de la función cos
Sabemos que para una función, el dominio son los valores de entrada permitidos y el rango es el valor de salida para esa entrada o valor de dominio en particular. Por lo tanto, podemos suponer que la función actúa como un procesador que recibe información, la procesa y genera una salida particular. El dominio y rango de la función cos se analiza a continuación:
- Dominio de la función coseno: R es decir, conjunto de todos los números reales.
- Rango de la función coseno: [-1, 1], es decir, la salida varía entre todos los números reales entre -1 y 1.
Período de una función coseno
El función es de naturaleza periódica, es decir, se repite después de 2π o 360°. En otras palabras, se repite después de cada rotación completa. Por tanto, el período de la función coseno es una rotación completa o un ángulo de 360° (o 2π).
Recíproco de una función coseno
El recíproco de una función coseno se conoce como secante función o segundo para abreviar. Matemáticamente, el recíproco de la función coseno viene dado como
tatuaje en forma completa
seg(θ) = 1/cos(θ)
Según reglas de Recíprocos , si multiplicamos el Cos x por Sec x el producto siempre será 1.
Gráfico de función coseno
La gráfica de la función coseno se parece a la gráfica de la función seno con la diferencia básica de que para x = 0 la gráfica de la función sen pasa desde el origen, mientras que en x = 0, la gráfica de la función coseno pasa desde (0, 1) en y-aixs. A continuación se muestra la gráfica del valor de la función coseno, es decir, y = cos x
Las propiedades discutidas anteriormente se pueden ver en el gráfico como la naturaleza periódica de la función.
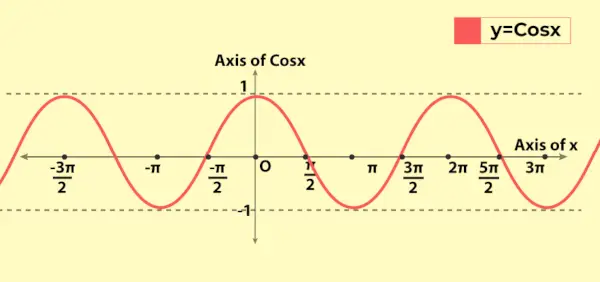
Variación de la función coseno en la gráfica
Dado que el rango de la función coseno es [-1, 1], varía de -1 a 1 en el gráfico. Muestra su naturaleza periódica ya que la gráfica se repite después de cada longitud 2π en el eje x. Esto refleja que la función coseno tiene un período de 2π (o 360°).
Cos en el círculo unitario
La función coseno se puede definir utilizando un círculo unitario. Entendamos cómo podemos definir la función coseno en términos de círculo unitario.

Considere un segmento de línea OA que gira alrededor del punto O donde O es el origen del plano cartesiano. Así, la rotación de OA describe un círculo unitario (círculo de radio unitario) centrado en el origen O y el punto A siempre se encuentra en este círculo. Si dejamos caer una perpendicular desde A en el eje x y llamamos B al punto de intersección, y θ es el ángulo que forma OA con la dirección positiva del eje x, entonces cos(θ) = proyección de la hipotenusa en x -eje = OB/|OA| = OB (ya que |OA| = 1 unidad).
Tenga en cuenta que la dirección OB es importante como se ve en las siguientes figuras. El segmento verde indica la longitud/magnitud y la flecha indica la dirección (+ve o -ve) de cos(θ)

Tenga en cuenta que el valor de cos(θ) es positivo para θ que pertenece al primer y cuarto cuadrante, mientras que negativo para θ que pertenece al segundo y tercer cuadrante.
Función inversa de coseno
La inversa de una función coseno conocida como arco-coseno función y abreviado como arccos(x) o porque -1 (X) se define de la siguiente manera
cos(x) = y
⇒ porque -1 (y) = x
Dominio y rango de la función coseno inverso
El dominio y el rango de la función coseno inverso se mencionan a continuación:
- Dominio de la función coseno inverso: Todos los números reales en el rango [-1, 1]
- Rango de función coseno inverso: Todos los números reales en el rango [0, π]
Función coseno hiperbólica
Las funciones hiperbólicas son equivalentes analógicos de la función trigonométrica cuya expresión algebraica está en términos de función exponencial. La función coseno hiperbólica abreviada como cosh(x) dónde X es un ángulo hiperbólico es un concepto de geometría hiperbólica. Como (cos(x), sin(x)) representa un punto en un círculo unitario, (cosh(x), sinh(x)) representa un punto en una hipérbola unitaria, es decir, xy = 1 donde sinh(x) representa hiperbólica función seno. La expansión algebraica de la función cos hiperbólica viene dada como
cosh(x) = (e X + y -X )/2
Más detalles sobre funciones hiperbólicas están fuera del alcance de este artículo, pero puede consultar Este artículo .
Función coseno en cálculo
La rama del cálculo en matemáticas se ocupa de la diferenciación e integración de una función dada. La diferenciación de funciones es la tasa de cambio de la función con respecto a la variable independiente, mientras que la integración es el proceso inverso de diferenciación que se ocupa de encontrar la integral de una función cuya derivada existe.
Derivada de la función coseno
El derivado de la función coseno es igual a negativo de la función seno. Matemáticamente
d(cos(x))/dx = -sin(x)
Integración de la función coseno.
El indefinite integral de la función coseno es igual a la función seno. Matemáticamente –
∫cos(x)dx = sin(x) + C, donde C es la constante de integración.
Funciones seno y coseno
El siguiente gráfico representa la diferencia clave entre la función seno y coseno:

Diferencia entre funciones seno y coseno
La siguiente tabla enumera las diferencias entre la función seno y coseno:
Función seno | Función coseno |
|---|---|
En un círculo unitario, el seno de un ángulo es la proyección de la hipotenusa sobre el eje y. | En un círculo unitario, el coseno de un ángulo es la proyección de la hipotenusa sobre el eje x. |
sin(θ) = Altura del triángulo rectángulo / Longitud de la hipotenusa | cos(θ) = Base del triángulo rectángulo / Longitud de la hipotenusa |
Su valor es 0 en 0°, 180° y 360°. | Su valor es 0 a 90° y 270°. |
Su valor es máximo, es decir, 1 a 90°. | Su valor es máximo, es decir, 1 en 0° y 360°. |
Su valor es mínimo, es decir, -1 a 270°. | Su valor es mínimo, es decir, -1 a 180°. |
Tabla de valores cos
La siguiente tabla proporciona los valores de la función coseno para algunos ángulos comunes en el primer cuadrante del plano cartesiano:
Ángulo en grados (θ) | Ángulo en radianes (x) | Cos (x) |
|---|---|---|
0 | 0 | 1 |
30 | p/6 | √3/2 |
45 | p/4 | 1/√2 |
60 | p/3 | 1/2 |
90 | p/6 | 0 |
Podemos calcular fácilmente los valores de otros ángulos comunes como 15°, 75°, 195°, -15°, etc. usando estos valores usando las fórmulas cos (x + y) y cos (x – y) que se describen más adelante en este artículo.
Controlar, Tabla trigonométrica
Identidades de funciones cos
Las identidades trigonométricas básicas relacionadas con la función coseno se mencionan a continuación:
- sin2(x) + cos2(x) = 1
- cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- cos(-x) = cos(x)
- cos(x) = 1/s(x)
- cos 2x = cos2x – sin2x = 1 – 2pecado2x = 2cos2x – 1 = (1 – tan2x/1 + tan2X)
- porque 3x = 4cos3x – 3cosx
Artículos relacionados
- Diferenciación de funciones trigonométricas
- Funciones trigonométricas inversas
- Derivados trigonométricos inversos
Ejemplos resueltos de función coseno
A continuación se muestran algunos ejemplos resueltos para ayudarle a comprender mejor el concepto de función coseno.
Ejemplo 1: ¿Cuáles son los valores máximo y mínimo de la función coseno?
Solución:
El valor máximo de la función coseno es 1 en 0° y 180° mientras que el valor mínimo de la función es -1 en 180°.
Ejemplo 2: ¿En qué ángulo(s) en el rango [0, 360] es 0 el valor de la función coseno?
Solución:
El valor de la función coseno es 0 en los ángulos 90° y 270°.
Ejemplo 3: ¿Para qué cuadrantes es negativo el valor de la función coseno?
Solución:
La función coseno es negativa en el II.Dakota del Nortey IIItercerocuadrantes.
Ejemplo 4: Calcular el valor de cos (45°).
Solución:
nodo de lista java
Según la identidad 4 dada anteriormente, cos(-x) = cos(x).
Por lo tanto, cos(-45°) = cos(45°) = 1/√2
Ejemplo 5: Calcular el valor de cos(15°).
Solución:
Usando la identidad 3 dada arriba –
cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}
Ejemplo 6: ¿Qué es cos? -1 (1/2) en el rango [0,π]?
Solución:
vamos porque-1(1/2) = y.
Por lo tanto, cos(y) = 1/2 ⇒ y = π/3 en el rango indicado anteriormente.
Por tanto la respuesta es π/3.
Ejemplo 7: ¿Cuál es el valor de cos(-15°)?
Solución:
Usando la identidad 3 dada arriba –
cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .Alternativamente, también podemos usar la identidad cos(-x) = cos(x) y usar el valor de cos(15°) calculado en el ejemplo 5.
Ejemplo 8: Calcule el área bajo la gráfica de la función coseno para x = 0 a x = π/2.
Solución:
El área dada se puede calcular resolviendo la siguiente integral definida:
int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1 Por lo tanto, la respuesta es 1 unidad cuadrada.
Ejemplo 9: Si cos(x) = π/3, encuentre el valor de cos(3x) (en forma decimal con precisión de dos dígitos decimales).
Solución:
Usando la identidad – cos(3x) = 4cos3(x) – 3cos(x) –
cos(3x) = 4⨉(π/3)3-3⨉(π/3) ≅ 4,59 – π = 1,45
Ejemplo 10: Encuentre el valor de cos(120°).
Solución:
Usando la identidad para cos(2x)
cos(120°) = cos(2⨉60°) = 1 – 2 sin2(60°) = 1- 2⨉(√3/2)2= 1 – 3/2 = -1/2
Preguntas de práctica: funciones cos
P1. ¿Cuál es la fórmula para calcular el coseno de un ángulo en un triángulo rectángulo?
P2. ¿Cuál es la interpretación geométrica de cos en el plano cartesiano?
P3. Calcula el valor de cos(120°).
P4. Encuentra el valor de cos -1 (√3/2) en el rango [π, 2π].
P5. Si un poste proyecta una sombra de la misma longitud sobre el suelo, encuentre el ángulo del sol con respecto al suelo si el sol está en dirección este.
Resumen: función coseno
La función coseno, denotada como cos(x), es una función trigonométrica fundamental definida como la relación entre la base y la hipotenusa en un triángulo rectángulo y es esencial en varios campos como la física, la ingeniería y la geometría debido a su naturaleza periódica. , que es fundamental para modelar el comportamiento de las olas. Tiene dominio de todos los números reales y un rango de -1 a 1, repitiendo su ciclo cada 2 Pi radianes o 360 grados, evidente por su gráfico ondulado que comienza en (0,1). En términos de cálculo, la derivada de cos(x) es − sin( X ), y su integral produce sin( X )+ C , con C como constante de integración. Esta función también se extiende a formas hiperbólicas, como cosh(x), mejorando su aplicación en diversos contextos y soluciones matemáticas, incluidos cálculos de ondas y oscilaciones en sistemas físicos.
Función coseno: preguntas frecuentes
1. ¿Qué es la función coseno?
La función coseno es una de las funciones trigonométricas fundamentales. Se define en un triángulo rectángulo como la relación entre la longitud del lado adyacente al ángulo en cuestión y la longitud de la hipotenusa.
2. ¿Son iguales cos y coseno en trigonometría?
Sí. cos es una abreviatura/forma corta de la función coseno.
3. ¿Cuál es el rango de la función Cos?
El rango de la función cos o coseno son todos los números reales que van de -1 a 1, es decir, [-1,1].
4. ¿Cuál es el dominio de la función Cos?
El dominio de la función cos o coseno es el ser de todos los números reales, es decir, R .
5. ¿Cuál es el valor máximo de la función coseno?
El valor máximo de la función coseno es 1 para todos los ángulos equivalentes a 0° o 360°.
6. ¿Cuál es el valor mínimo de la función coseno?
El valor mínimo de la función coseno es -1 para todos los ángulos equivalentes a 180°.
7. ¿Cómo encontrar el valor de Cos(-x)?
El valor de cos(-x) se puede calcular calculando el valor de cos(x) debido a la existencia de la siguiente identidad: cos(-x) = cos(x).
8. ¿Cómo graficar la función coseno?
Para dibujar la gráfica de la función coseno en un plano cartesiano, consulte el eje x como representación de los ángulos en radianes (o grados) y el eje y como representación de los valores de la función coseno para el ángulo correspondiente en el eje x. Ahora,
- Paso 1: Tome un subconjunto del eje x para el cual le gustaría dibujar el gráfico.
- Paso 2: Divida el eje x en este rango en puntos equidistantes (es decir, hay un espacio igual entre todos los subpuntos). Tenga en cuenta que cuanto mayor sea el número de divisiones, mayor será la precisión del gráfico resultante.
- Paso 3: Para cada uno de estos subpuntos x, marca el punto (x, cos(x)) en la gráfica.
- Etapa 4: Une todos los puntos marcados para obtener la gráfica de la función coseno (para el subconjunto del eje x que seleccionaste).
9. ¿Cómo encontrar el período de una función coseno?
El período de una función coseno se refiere al rango mínimo de valores después del cual la función comienza a repetirse. Sabemos que la función coseno se repite después de cada rotación completa, lo que significa 2π radianes. Por tanto, el período de la función coseno es 2π radianes o 360°.
10. ¿Qué es la amplitud de una función coseno?
La amplitud de una función coseno se refiere al desplazamiento máximo del valor de la función desde la posición media, es decir, el eje x. La amplitud de la función coseno es 1 ya que el desplazamiento máximo es 1 (para los valores -1 y 1 a 180 y 0 grados respectivamente. Tenga en cuenta que el rango de la función coseno es [-amplitud, amplitud].
