Tabla de trigonometría es una tabla estándar que nos ayuda a encontrar los valores de razones trigonométricas para ángulos estándar como 0°, 30°, 45°, 60° y 90°. Él consta de las seis razones trigonométricas: seno, coseno, tangente, cosecante, secante y cotangente.
Aprendamos sobre la tabla de trigonometría en detalle.
Tabla de contenidos
- Tabla de trigonometría
- Tabla de funciones trigonométricas
- Truco para aprender razones trigonométricas
- Cómo memorizar la tabla trigonométrica
- Cómo crear una tabla trigonométrica
- Fórmulas trigonométricas
- Tabla de identidades trigonométricas
- Ejemplos de tablas trigonométricas
Tabla de trigonometría
La tabla trigonométrica es la disposición de los valores de las seis funciones trigonométricas para sus ángulos comunes en forma tabulada.
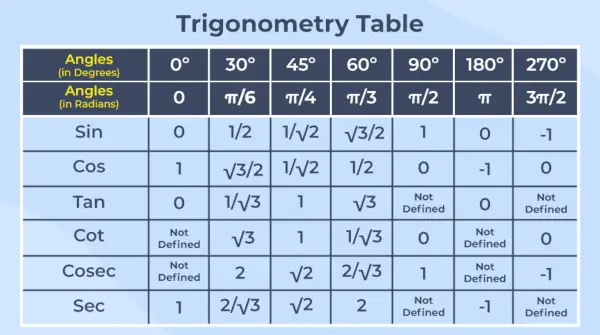
Nota – La trigonometría es una rama de las matemáticas que se ocupa de las relaciones entre los ángulos y los lados de los triángulos rectángulos.
Tabla de funciones trigonométricas
La trigonometría tiene 6 funciones trigonométricas básicas: seno, coseno, tangente, cosecante, secante y cotangente. Ahora veamos las funciones trigonométricas.
Para cualquier triángulo rectángulo con perpendicular (P), base (B) e hipotenusa (H), las seis funciones trigonométricas son las siguientes:
| Tabla de funciones trigonométricas | |||
| Función | Definición | Representación | Relación con los lados de un triángulo rectángulo |
| Su | Relación de perpendicular e hipotenusa. | sin i | Lado opuesto / Hipotenusa |
| Coseno | Relación de base e hipotenusa | porque i | Lado adyacente / Hipotenusa |
| Tangente | Relación del seno y el coseno de un ángulo. | tan i | Lado opuesto / Lado adyacente |
| Cosecante | Recíproco del pecado θ | csc i o cosec i | Hipotenusa / Lado opuesto |
| Secante | Recíproco de cos θ | segundo i | Hipotenusa / Lado adyacente |
| Cotangente | Recíproco de tan θ | cuna i | Lado adyacente / Lado opuesto |
Nota – La trigonometría es una rama de las matemáticas que se ocupa de las relaciones entre los ángulos y los lados de los triángulos, particularmente los triángulos rectángulos. Implica el estudio y la aplicación de seno, coseno, tangente y otras funciones trigonométricas para resolver problemas en diversos campos.
Controlar : Trigonometría: fórmulas, tablas, identidades y razones
Truco para aprender razones trigonométricas
Estudie la tabla que se analiza a continuación para aprender las razones trigonométricas de una manera fácil de recordar.
| Algunas personas tienen el pelo negro y rizado para producir belleza. |
| pecado θ (Algunos) = Perpendicular(personas) / hipotenusa(tener) |
| cos θ (rizado) = Base (negro) / hipotenusa (cabello) |
| tan θ (to) = Perpendicular(producir) / Base(belleza) |
Cómo memorizar la tabla trigonométrica
La tabla de trigonometría es bastante fácil de recordar si conoces todas las fórmulas de trigonometría. También hay un truco llamado truco de una mano memorizar la tabla de trigonometría.

Paso 1: En la figura anterior, para la tabla de senos, cuente los dedos del lado izquierdo para el ángulo estándar.
Paso 2: Divide el número de dedos del lado izquierdo (calcula en el primer paso) entre 4
Paso 3: Encuentre la raíz cuadrada del valor calculado en el Paso 2.
Controlar: Fórmulas trigonométricas: lista de todas las identidades y fórmulas trigonométricas
Cómo crear una tabla trigonométrica
Estudie los siguientes pasos para crear la tabla trigonométrica de ángulos estándar.
Paso 1: crear la tabla
Crea una tabla y enumera todos los ángulos, como 0°, 30°, 45°, 60° y 90°, en la fila superior. Ingrese todas las funciones trigonométricas sin, cos, tan, cosec, sec y cot en la primera columna.
Paso 2: Evalúa el valor de todos los ángulos de la función sin.
Para encontrar los valores de la función sin, divida 0, 1, 2, 3 y 4 entre 4 y tome la raíz de cada valor, respectivamente como,
Porque el valor de sin 0° = √(0/4) = 0
Similarmente,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| sin 0° | sin 30° | sin 45° | sin 60° | sin 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Paso 3: Evaluar el valor de todos los ángulos de la función cos.
El valor de la función cos es opuesto al valor de la función sen, es decir, cos 0° = sen 90°, cos 30° = sen 60° y cos 45° = sen 45°, entonces
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Paso 4: Evalúa el valor de todos los ángulos de la función tan
El valor de la función tan es igual a la función sin dividida por la función cos, es decir, tan x = sin x / cos x. El valor de todos los ángulos en la función tan se calcula como,
tan 0°= sin 0° / cos 0° = 0/1 = 0, similarly
| tan 0° | tan 30° | tan 45° | tan 60° | tan 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | No definida |
Paso 5: Evalúa el valor de todos los ángulos de la función cosec
El valor de la función cosec es igual al recíproco de la función sin. El valor de cosec 0° se obtiene tomando el recíproco de sen 0°
cosec 0° = 1 / sen 0° = 1 / 0 = No Definido. Similarmente,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| No definida | 2 | √2 | 2/√3 | 1 |
Paso 6: Evalúa el valor de todos los ángulos de la función sec.
El valor de la función sec es igual al recíproco de la función cos. El valor de sec 0° se obtiene tomando el recíproco de cos 0°
sec 0° = 1 / cos 0° = 1 / 1 = 1. De manera similar,
| segundos 0° | segundos 30° | segundos 45° | segundos 60° | segundos 90° |
|---|---|---|---|---|
| 1 | 2/√3 | √2 | 2 | No definida |
Paso 7: Evaluar el valor de todos los ángulos de la función cuna
El valor de la función cot es igual al recíproco de la función tan. El valor de cot 0° se obtiene tomando el recíproco de tan 0°
cuna 0° = 1 /tan 0° = 1 / 0 = No definido. Similarmente,
| cuna 0° | cuna 30° | cuna 45° | cuna 60° | cuna 90° |
|---|---|---|---|---|
| No definida | √3 | 1 | 1/√3 | 0 |
De esta forma, podemos crear la siguiente tabla de razones trigonométricas:
| Tabla trigonométrica de grados y radianes | |||||||
|---|---|---|---|---|---|---|---|
| Ángulo (en grados) | Ángulo (en radianes) | Sin | porque | Tan | Cosec | Segundo | Cuna |
| 0° | 0 | 0 | 1 | 0 | Indefinido | 1 | Indefinido |
| 30° | p/6 | 1/2 | √3/2 | 1/√3 | 2 | 2/√3 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 2/√3 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Indefinido | 1 | Indefinido | 0 |
Fórmulas trigonométricas
Aprendamos sobre algunas fórmulas de trigonometría relacionadas con los ángulos complementarios y suplementarios.
- Ángulos complementarios: Par de ángulos cuya suma es igual a 90°
- Ángulos suplementarios: Par de ángulos cuya suma es igual a 180°
Controlar: Razones trigonométricas
Identidades trigonométricas de ángulos complementarios
Las identidades de los ángulos complementarios se basan en la relación entre las funciones trigonométricas de dos ángulos que suman 90 grados (o π/2 radianes). Estos se conocen como identidades de cofuncion .
| Funcion trigonometrica | Identidad |
|---|---|
| Su | sin(90°− i )=porque i |
| Coseno | cos(90°- i )=sin i |
| Tangente | tan(90°− i )=cuna i |
| Cotangente | cuna(90°- i )=tan i |
| Secante | seg(90°- i )=csc i |
| Cosecante | cosec(90°- i )=seg i |
Identidades trigonométricas de ángulos suplementarios
Las identidades de los ángulos suplementarios se relacionan con las funciones trigonométricas de dos ángulos que suman 180 grados (o π radianes).
| Funcion trigonometrica | Identidad |
|---|---|
| Su | sin(180°− i )=sin i |
| Coseno | cos(180°- i )=−cos i |
| Tangente | tan(180°− i )=−tan i |
| Cotangente | cuna(180°- i )=−cuna i |
| Secante | seg(180°- i )=−seg i |
| Cosecante | cosec(180°- i )=cosec i |
Tabla de identidades trigonométricas
Identidades trigonométricas son las identidades que se utilizan mucho en la resolución de problemas trigonométricos. Hay varias identidades trigonométricas, pero las tres identidades trigonométricas principales son,
| Tabla de identidades trigonométricas | |
| Identidad trigonométrica | Fórmula |
| Identidad pitagórica | sin2θ + porque2θ = 1 |
| Identidad secante-tangente | segundo2θ – tan2θ = 1 |
| Identidad cosecante-cotangente | cosec2θ – cuna2θ = 1 |
Además, consulte:
- Razones trigonométricas
- Identidades trigonométricas inversas
- Alturas y distancias
Ejemplos de tablas trigonométricas
Resolvamos algunas preguntas sobre la tabla trigonométrica.
Ejemplo 1: Si sen θ = 4/5, entonces encuentre todos los valores trigonométricos.
Solución:
Aquí tenemos,
pecado θ = 4/5
as, sin θ = Perpendicular / Hypotenuse
entonces tenemos Perpendicular (P) = 4 e hipotenusa (H) = 5
Entonces según el teorema de Pitágoras h 2 =P 2 +B 2
Averigüemos el valor de la base (B)
52=B2+ 42
25 = segundo2+ 16
25-16 = segundo2
B2= 9
B = 3Ahora tenemos,
Sin θ = Perpendicular/Hypotenuse
= AB/CA = 4/5Coseno θ = Base/Hipotenusa
= BC/AC = 3/5Tangente θ = Perpendicular/Base
= AB/BC = 4/3Cosecante θ = Hipotenusa/Perpendicular
= CA/AB = 5/4Secante θ = Hipotenusa/Base
= CA/BC = 5/3Cotangente θ = Base/Perpendicular
= BC/AB = 3/4
Ejemplo 2: Encuentre el valor de cos 45° + 2 sen 60° – tan 60°.
Solución:
De la tabla de trigonometría,
cos 45° = 1/√2, sin 60° = √3/2 and tan 60° = √3
De este modo,
cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Ejemplo 3: Encuentre el valor de cos 75°.
Solución:
Lo sabemos,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Conclusión – Tabla de trigonometría
La tabla de trigonometría proporciona una referencia completa para las funciones trigonométricas seno, coseno, tangente, cosecante, secante y cotangente, junto con sus respectivos valores para varios ángulos. I Sirve como una valiosa herramienta para resolver ecuaciones trigonométricas, análisis de relaciones geométricas y comprensión del comportamiento de fenómenos periódicos. Ya sea en Matemáticas, física, ingeniería u otros campos, la tabla de trigonometría ayuda en los cálculos, la resolución de problemas y la visualización, contribuyendo a una comprensión más profunda de los conceptos trigonométricos y sus aplicaciones en escenarios del mundo real.
números abc
Tabla de trigonometría – Preguntas frecuentes
¿Qué es la trigonometría?
La trigonometría es la rama de las matemáticas que se ocupa de los ángulos y lados de cualquier triángulo.
¿Qué es una tabla trigonométrica?
La tabla de trigonometría es una tabla que contiene los valores de las seis funciones trigonométricas para los ángulos comunes.
¿Quién inventó la mesa de trigonometría?
El astrónomo griego Hiparco (127 a. C.) inventó la tabla de trigonometría.
¿Qué son los ángulos estándar en una tabla trigonométrica?
Los ángulos estándar en una tabla trigonométrica son 0°, 30°, 45°, 60° y 90°.
¿Cuál es el valor de tan 45 grados?
El valor de tan 45 grados es 1.
¿Cómo aprender la tabla de trigonometría?
El truco para aprender la tabla trigonométrica es:
- Tienes que aprender todos los valores de todos los ángulos de la función sin.
- El valor de todos los ángulos de la función cos es la imagen especular de la función sin.
- Los valores de la función tan se pueden calcular dividiendo la función sin por la función cos.
- El valor de la función cosec es recíproco del pecado.
- De manera similar, sec y cot son recíprocos de las funciones cos y cot.
¿Cuáles son las seis funciones básicas en la tabla trigonométrica?
Las seis funciones trigonométricas básicas de la tabla trigonométrica son seno, coseno, tangente, secante, cotangente y cosecante.
¿Existen calculadoras que puedan reemplazar las tablas de trigonometría?
Las calculadoras científicas pueden calcular razones trigonométricas para cualquier ángulo8.
¿Para qué sirve una tabla de trigonometría?
La tabla de trigonometría se utiliza básicamente para encontrar los valores de todas las razones trigonométricas para todos los ángulos. Estos valores tienen varias aplicaciones en la vida real.
