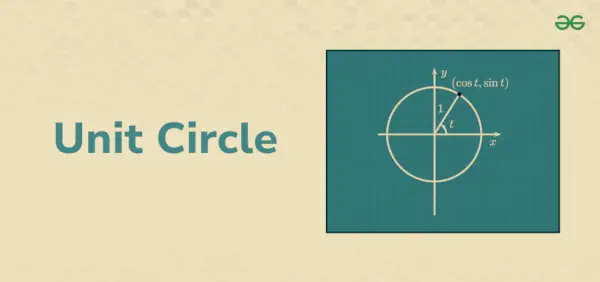
El círculo unitario es un círculo cuyo radio es 1. El centro del círculo unitario está en el origen (0,0) del eje. El circunferencia del círculo unitario es 2π unidades, mientras que el área del círculo unitario es π unidades2. Lleva todas las propiedades de Circle. El círculo unitario tiene la ecuación x2+ y2= 1. Este círculo unitario ayuda a definir varios conceptos trigonométricos.
Circulo unitario
El círculo unitario a menudo se denota como S1la generalización a dimensiones superiores es la esfera unitaria. Comprendamos más sobre el círculo unitario, la fórmula y los ejemplos resueltos en detalle a continuación.
¿Qué es el círculo unitario?
Un círculo unitario es un círculo que tiene un radio de una (1) unidad. Usamos el plano cartesiano para dibujar un círculo unitario y un círculo unitario es un polinomio de 2 grados con dos variables. El círculo unitario tiene varias aplicaciones en trigonometría y álgebra y se usa principalmente para encontrar los valores de diferentes razones trigonométricas como sen x, cos x, tan x y otras.
Definición del círculo unitario
En Matemáticas, definimos un círculo unitario como el lugar geométrico de un punto fijo que está a una distancia de una unidad del centro del círculo. Un círculo unitario tiene un radio de una unidad y de ahí el nombre de círculo unitario.
Ecuación del círculo unitario
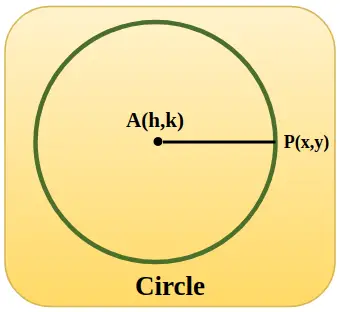
Sabemos que la ecuación de cualquier círculo con centro (h, k) y radio 'r' es,
(x-h) 2 + (y – k) 2 =r 2
Para un círculo unitario sabemos que r es 1 unidad, por lo que la ecuación del círculo unitario es,
(x-h) 2 + (y – k) 2 = 1
Fórmula del círculo unitario
Si el centro del círculo unitario es el origen, es decir (h, k) = (0, 0), entonces la ecuación del círculo unitario es,
X 2 + y 2 = 1
Un círculo unitario está representado en la imagen agregada a continuación, con coordenadas centrales h, k y cuando el círculo está en el origen el valor de h y k es cero y el radio AP es igual a 1 unidad.
Funciones trigonométricas usando el círculo unitario
La aplicación del teorema de Pitágoras en un círculo unitario puede utilizarse mejor para comprender las funciones trigonométricas. Para ello, consideramos un triángulo rectángulo colocado dentro de un círculo unitario en el plano de coordenadas cartesiano. Si nos fijamos, el radio de este círculo denota la hipotenusa del triángulo rectángulo.
El radio del círculo forma un vector. Esto conduce a la formación de un ángulo, digamos θ con el eje x positivo. Supongamos que x es la longitud de la base y y es la longitud de la altitud del triángulo rectángulo, respectivamente. Además, las coordenadas de los puntos finales del vector de radio son (x, y) respectivamente.
El triángulo rectángulo tiene los lados 1, x e y respectivamente. La razón trigonométrica se puede calcular ahora de la siguiente manera:
sin θ = Altitude/Hypotenuse = y/1
cos θ = Base/Hipotenusa = x/1
Ahora,
- sin θ = y
- porque θ = x
- tan θ = sin θ /cos θ = y/x
Al sustituir los valores de θ, podemos obtener valores principales de todas las funciones trigonométricas. Se encuentran valores similares de funciones trigonométricas en diferentes valores.
Círculo unitario con seno cos y tan
Cualquier punto del círculo unitario con coordenadas (x, y) se representa mediante identidades trigonométricas como (cosθ, sinθ). Las coordenadas de las esquinas del radio representan el coseno y el seno de los valores de θ para un valor particular de θ y la línea del radio. Tenemos cos θ = x y sen θ = y. Hay cuatro partes de un círculo, cada una de las cuales se encuentra en un cuadrante, formando un ángulo de 90°, 180°, 270° y 360°. Los valores del radio se encuentran entre -1 y 1 respectivamente. Además, los valores de sen θ y cos θ se encuentran entre 1 y -1 respectivamente.
Círculo unitario e identidades trigonométricas
Las identidades trigonométricas del círculo unitario para cotangente, secante y cosecante se pueden calcular utilizando las identidades para sen, cos y tan. En conclusión, obtenemos un triángulo rectángulo con los lados 1, xey respectivamente. Calcular las identidades del círculo unitario se puede expresar como,
- sin θ = y/1
- porque θ = x/1
- tan θ = y/x
- segundo θ = 1/x
- cosec θ = 1/y
- cot θ = x/y
Gráfico de círculo unitario
El gráfico de círculo unitario es un gráfico que contiene el valor de la función trigonométrica seno y coseno para varios ángulos. El gráfico de círculo unitario para el mismo se agrega a continuación,
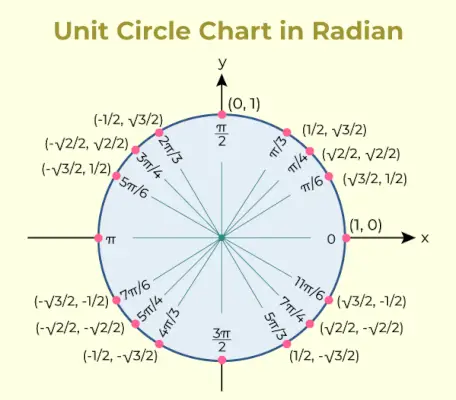
Tabla de círculo unitario
Las razones trigonométricas utilizadas en la tabla del círculo unitario se utilizan para enumerar las coordenadas de los puntos en el círculo unitario que corresponden a ángulos comunes.
| Anglos | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| porque java matemáticas pow | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| tan | 0 | 1/√(3) | 1 | √(3) | No definida |
| csc | No definida | 2 | √(2) | 2/√(3) | 1 |
| segundo | 1 | 2/√(3) | √(2) | 2 | No definida |
| cuna | No definida | √(3) | 1 | 1/√(3) | 0 |
Identidades pitagóricas del círculo unitario
Hay tres identidades pitagóricas y todas ellas se prueban fácilmente utilizando el concepto de círculo unitario. Las tres identidades pitagóricas son:
- sin2θ + porque2θ = 1
- 1 + tan2θ = segundo2i
- 1 + cuna2θ = cosec2i
Plano complejo del círculo unitario
Números complejos y Plano complejo se explican fácilmente utilizando el concepto de círculo unitario. La ecuación del círculo unitario en forma compleja es,
|z| = 1
O
X 2 + y 2 = 1
En la forma de Euler, el número complejo se representa como,
z = mi él = porque t + i(sen t)
Leer más
Ejemplos resueltos en círculo unitario
Q1: Demuestre que el punto Q se encuentra en un círculo unitario, Q = [1/√(6), √4/√6]
Solución:
Dado,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
La ecuación del círculo unitario es,
X2+ y2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Por tanto, el punto Q[1/√(6), √4/√6] no se encuentra en el círculo unitario.
Q2: Compute tan 30 oh usando los valores de sen y cos del círculo unitario.
Solución:
tan 30° usando valores de sen y cos,
tan 30° = (sin 30°)/ (cos 30°)
- sin 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
tan 30° = 1/√(3)
P3: Validar si el punto P [1/2, √(3)/2] se encuentra en el círculo unitario.
Solución:
Dado,
PAG = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
La ecuación del círculo unitario es,
- X2+ y2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= lado derecho
Preguntas de práctica sobre el círculo unitario
P1. Compruebe si los puntos A (1/2, 3/2) se encuentran en un círculo unitario.
P2. Compruebe si los puntos A (2, 1/2) se encuentran en un círculo unitario.
P3. Encuentra el valor de cos 240°
P4. Encuentra el valor de tan 320°
P5. Encuentra el valor del sen 160°.
Círculo unitario – Preguntas frecuentes
¿Qué es el círculo unitario?
Un círculo unitario se define como la ubicación de un punto a una unidad de distancia de un punto fijo. Tiene un centro en (0,0) y el valor de su radio es 1.
¿Cómo comprobar si un punto se encuentra en el círculo unitario?
Cualquier punto que se encuentre en un plano 2D y que tenga la forma (x, y) se expresa en la ecuación del círculo unitario x.2+ y2= 1 para verificar si se encuentra en el círculo o no.
¿Cuál es la fórmula del círculo unitario?
La fórmula del círculo unitario es una fórmula que se utiliza para representar algebraicamente un círculo unitario. La fórmula del círculo unitario se da como,
X 2 + y 2 = 1
¿Por qué se llama círculo unitario?
Un círculo unitario se llama círculo unitario porque tiene un radio de una (1) unidad.
