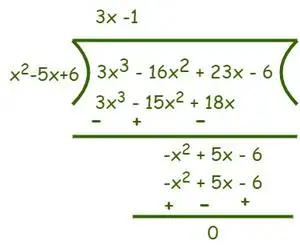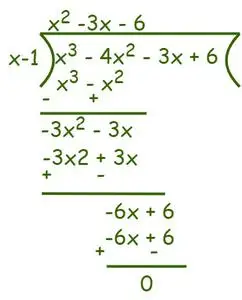Ecuación cúbica es una ecuación matemática en la que un polinomio de grado 3 se equipara con una constante u otro polinomio de grado máximo 2. La representación estándar de la ecuación cúbica es hacha ³ +bx ² +cx+d = 0 donde a, b, cyd son números reales. Algunos ejemplos de ecuación cúbica son X ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 etc.

Tabla de contenidos

• Definición de polinomio
• Grado de ecuación
• Definición de ecuación cúbica
• ¿Cómo resolver ecuaciones cúbicas?
• Resolver ecuaciones cúbicas
• Resolver ecuaciones cúbicas usando factores
• Resolver ecuaciones cúbicas mediante el método gráfico
• Problemas basados ​​en la resolución de ecuaciones cúbicas
• Problemas de práctica para resolver ecuaciones cúbicas

Para aprender a resolver ecuaciones cúbicas, primero debemos aprender sobre polinomios, el grado del polinomio y otros. En este artículo, aprenderemos sobre polinomios, ecuaciones polinomiales, resolución de ecuaciones cúbicas o cómo resolver ecuaciones cúbicas, y otros en detalle.

Definición de polinomio

El polinomio se define de la siguiente manera,

A polinomio es una expresión algebraica en la que la potencia de una variable es un número entero no negativo. La forma general de un polinomio es₀X^norte+ un₁X^n-1+ un₂X^n-2+… + un_norte. Dependiendo de la potencia máxima de la variable, un polinomio se puede clasificar como monomio, binomio, trinomio, etc.

¿Qué es una ecuación?

Una ecuación se define de la siguiente manera,

Una ecuación es un polinomio que se equipara a un valor numérico o a cualquier otro polinomio. Por ejemplo, x + 2 es un polinomio pero x + 2 = 5 es una ecuación. De manera similar, 2x + 3 = x + 1 también es una ecuación, mientras que 2x + 3 y x + 1 son polinomios individualmente.

Grado de ecuación

La definición del Grado de Ecuación se establece a continuación:

Grado de una ecuación se define como la potencia máxima que posee la variable en una ecuación.

Según el grado de la ecuación, una ecuación se puede clasificar de la siguiente manera:

• Ecuación lineal
• Ecuación cuadrática
• Ecuación cúbica
• Ecuación bicuadrática

Ecuación lineal

La ecuación en la que la potencia máxima de la variable es 1 se llama ecuación lineal.

• Por ejemplo 3x +1 = 0

Polinomio cuadrático

La ecuación en la que la potencia máxima de la variable es 2 es una ecuación cuadrática.

• Por ejemplo 3x²+x+1 = 0

Ecuación cúbica

La ecuación en la que la potencia máxima de la variable es 3 se llama ecuación cúbica.

• Por ejemplo 5x³+3x²+x+1 = 0

Polinomio bicuadrático

La ecuación en la que la potencia máxima de la variable es 4 se llama polinomio bicuadrático o polinomio cuártico.

• Por ejemplo 5x⁴+4x³+3x²+2x+1 = 0

Definición de ecuación cúbica

Ecuación cúbica es una ecuación algebraica donde el grado más alto del polinomio es 3. Algunos ejemplos de ecuaciones cúbicas son 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0,etc.

La forma general de una ecuación cúbica es,

hacha ³ + bx ² + cx + d = 0, a ≠ 0

Dónde,

• a, b, y C son los coeficientes de la variable y sus exponentes y d es la constante y
• a B C y d son números reales.

¿Cómo resolver ecuaciones cúbicas?

Una ecuación cúbica es una ecuación de grado tres. Tiene tres soluciones y se puede resolver fácilmente siguiendo los pasos que se agregan a continuación,

Paso 1: Encuentre una solución a la ecuación cúbica mediante el método de intentarlo y probarlo. Supongamos que tenemos una ecuación cúbica P(x), luego encuentre para cualquier x = a, P(a) = 0 tomando, x = 0, ±1, ±2, ±3,… y así.

Paso 2: Cuando obtengamos P(a) = 0, encuentre el factor (x – a) de P(x)

Paso 3: Divida P(x) por (x – a) para obtener una ecuación cuadrática, digamos Q(x), usando división polinómica.

Etapa 4: Factariza la ecuación cuadrática Q(x) para obtener los factores como (x – b) y (x – c).

Paso 5: (x – a), (x – b) y (x – c) son los factores de P(x) y al resolver cada factor obtenemos las raíces de la ecuación como, a, b y c.

Aprender más acerca de, Polinomio divisorio

Resolver ecuaciones cúbicas

A Ecuación cúbica se puede resolver mediante dos métodos

• Reduciéndolo a una ecuación cuadrática y luego resolviéndolo mediante factorización o mediante la fórmula cuadrática
• Por método gráfico

A Ecuación cúbica tiene tres raíces. Estas raíces pueden ser reales o imaginarias. Además, puede haber raíces distintas o dos raíces iguales y una diferente y las tres raíces iguales.

Cabe señalar que para cualquier ecuación, incluida Ecuaciones cúbicas , la ecuación siempre debe ordenarse en su forma estándar antes de resolverla.

Por ejemplo, si la ecuación dada es 2x²-5 = x + 4/x, entonces tenemos que reorganizar esto en su forma estándar, es decir, 2x³-X²-5x-4 = 0. Ahora podemos resolver la ecuación usando cualquier método apropiado.

Resolver ecuaciones cúbicas usando factores

La solución de la ecuación cúbica usando el teorema del factor se explica usando el ejemplo agregado a continuación,

Ejemplo: encontrar las raíces de la ecuación f(x) = 3x ³ −16x ² + 23x − 6 = 0.

Solución:

Expresión dada: f(x) = 3x³−16x²+ 23x − 6 = 0

convertir cadena a carácter

Primero, factoriza el polinomio para obtener raíces.

Como la constante es -6 los factores posibles son 1, 2, 3, 6.

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Sabemos que, según Teorema de los factores si f(a) = 0, entonces (xa) es un factor de f(x)

Entonces, (x – 2) y (x – 3) son factores de f(x). Por tanto, el producto de (x – 2) y (x – 3) también será factor de f(x). Ahora, para encontrar los factores restantes, use el método de división larga y divida f(x) por el producto de (x – 2) y (x – 3)

Por lo tanto, Divisor = (x – 2)(x – 3) = (x²– 5x + 6) y Dividendo = 3x³−16x²+ 23x − 6. Ahora divide como se muestra a continuación,

Después de la división obtenemos (3x- 1) como cociente y el resto es 0. Ahora según Algoritmo de división lo sabemos Dividendo = Divisor×Cociente+Restante.

⇒f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Dado que f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒x²– 5x + 6 = 0 o 3x-1 = 0

Ahora tomaremos 3x-1 = 0 ⇒ x = 1/3 como ya conocemos dos raíces de x²– 5x + 6 que son 2 y 3

Entonces,

Raíces de lo dado Ecuación cúbica son 1/3, 2 y 3.

Resolver ecuaciones cúbicas mediante el método gráfico

Una ecuación cúbica se resuelve gráficamente cuando no se puede resolver la ecuación dada usando otras técnicas. Entonces, necesitamos un dibujo preciso de la ecuación cúbica dada. Las raíces de la ecuación son los puntos en los que la gráfica cruza el eje X si la ecuación está en términos de x y si la ecuación está en términos de y entonces las raíces de la ecuación son los puntos en los que la gráfica corta el eje Y.

El número de soluciones reales de la ecuación cúbica es igual al número de veces que la gráfica de la ecuación cúbica cruza el eje X.

Ejemplo: encontrar las raíces de la ecuación f(x) = x ³ − 4x ² − 9x + 36 = 0, utilizando el método gráfico.

Solución:

Expresión dada: f(x) = x³− 4x²− 9x + 36 = 0.

Ahora, simplemente sustituye x por valores aleatorios en la gráfica de la función dada:

X	-4	-3	-2	-1	0	1	2	3	4	5
f(x) serial en postgres	-56‬	0	19‬	40	36	24‬	10‬	0	0	16

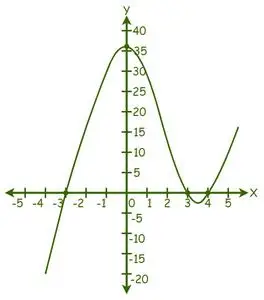
Podemos ver que la gráfica ha cortado el eje X en 3 puntos, por lo tanto, existen 3 soluciones reales.

Según el gráfico, las soluciones son: x = -3, x = 3 y x = 4.

Por tanto, las raíces de la ecuación dada son -3, 3 y 4.

Leer más,

• Ecuación lineal
• Resolver ecuaciones cuadráticas
• Factorizar polinomios

Problemas basados ​​en la resolución de ecuaciones cúbicas

Problema 1: Encuentra las raíces de f(x) = x ³ – 4x ² -3x + 6 = 0.

Solución:

Expresión dada: f(x) = x³– 4x²-3x + 6 = 0.

Primero, factoriza el polinomio para obtener raíces.

Como la constante es +6, los factores posibles son 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Entonces, según Teorema de los factores (x – 1) es un factor de la ecuación dada. Ahora, para encontrar los factores restantes, utilice el método de división larga.

De acuerdo a Algoritmo de división podemos escribir,

Entonces, f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 o (x²– 3x – 6) = 0

Sabemos que las raíces de una ecuación cuadrática ax²+ bx + c = 0 son,

x = [-b ± √(b²-4ac)]/2a

Por tanto, para (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Por lo tanto, las raíces de la ecuación cúbica dada son 1, (3+√33)/2 y (3–√33)/2.

Problema 2: Encuentra las raíces de la ecuación f(x) = 4x ³ – 10x ² + 4x = 0.

Solución:

Expresión dada: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 o 4x – 2 = 0, x – 2 = 0

⇒ x = 0 o x = 1/2 o x = 2

Por tanto, las raíces de la ecuación dada son 0, 1/2 y 2.

Problema 3: Encuentra las raíces de la ecuación f(x) = x ³ + 3x ² + x + 3 = 0.

Solución:

Expresión dada: f(x) = x³+ 3x²+ x + 3 = 0.

⇒x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+ 1) = 0

⇒ x + 3 = 0 o x²+ 1 = 0

⇒ x = -3, ±i

Entonces, la ecuación dada tiene una raíz real, es decir, -3, y dos raíces imaginarias, es decir, ±i.

Problema 4: Encuentra las raíces de la ecuación f(x) = x ³ – 7x ² – x + 7 = 0.

Solución:

Expresiones dadas,

f(x) = x³– 3x²– 5x + 7 = 0

Primero, factoriza la ecuación, f(x): x³– 3x²– 5x + 7= 0

Se puede factorizar en (x-7)(x+1)(x-1) = 0

Después de factorizar el polinomio, podemos encontrar las raíces igualando cada factor a cero. Por ejemplo:

• x – 7 = 0, entonces x = 7
• x + 1 = 0, entonces x = -1
• x – 1 = 0, entonces x = 1

Entonces las raíces de la ecuación f(x): x³– 3x²– 5x + 7 = 0 son

• x = 7
• x = -1
• x = 1

Problema 5: Encuentra las raíces de la ecuación f(x) = x ³ − 6x ² + 11x − 6 = 0, usando el método gráfico.

Solución:

Expresión dada: f(x) = x³− 6x²+ 11x − 6 = 0.

Ahora, simplemente sustituye x por valores aleatorios en la gráfica de la función dada:

X	1	2	3	4	5
f(x)	0	0	0	6	24

Podemos ver que la gráfica ha cortado el eje X en 3 puntos, por lo tanto, existen 3 soluciones reales.

Según la gráfica, las soluciones son: x = 1, x = 2 y x = 3.

Por tanto, las raíces de la ecuación dada son 1, 2 y 3.

Problemas de práctica para resolver ecuaciones cúbicas

A continuación se agregan varios problemas de práctica relacionados con ecuaciones cúbicas. Resuelva estos problemas para comprender completamente el concepto de ¿Cómo resolver ecuaciones cúbicas?

P1. Resuelve la ecuación cúbica, 3x³+ 2x²– 11x + 7 = 0.

P2. Encuentra las raíces de la ecuación cúbica, 4x.³– 12x²+ 17 = 0.

P3. Resuelve la ecuación cúbica, x³+ 4x²– x + 3 = 0 usando el método gráfico.

P4. Encuentra el número que satisface, -9x³+ 11x²– 8x + 2 = 0.

Preguntas frecuentes sobre la resolución de ecuaciones cúbicas

1. ¿Qué son las ecuaciones cúbicas?

Las ecuaciones cúbicas son las ecuaciones algebraicas en las que la potencia máxima de una variable es 3.

2. ¿Cómo se factoriza una ecuación cúbica?

Podemos factorizar una ecuación cúbica de dos maneras. Primero, tomando una expresión lineal común de la ecuación cúbica dada, luego tendremos una expresión lineal y una cuadrática como producto. Esta ecuación cuadrática se puede factorizar aún más para obtener todos los factores. El segundo método consiste en encontrar un cero de la ecuación cúbica dada poniendo valores aleatorios. El valor para el cual obtenemos que el valor de la ecuación sea cero será uno de los ceros de la ecuación cúbica dada. Ahora, usando el teorema del factor, forme una expresión lineal, digamos x-a y divida la ecuación cúbica dada por esta expresión, lo que dará como cociente una ecuación cuadrática. Esta ecuación cuadrática obtenida se puede factorizar aún más para obtener todos los factores.

3. ¿Cómo se resuelve gráficamente una ecuación cúbica?

Para resolver una ecuación cúbica gráficamente, coloque valores aleatorios para x en la ecuación cúbica dada y resuelva, obtendrá los valores de y. Trace estos valores obtenidos en la gráfica. Encuentra las coordenadas en las que la gráfica se cruza con el eje x. Estas coordenadas son la solución de la ecuación cúbica.

4. ¿Se pueden resolver exactamente todas las ecuaciones cúbicas?

Cualquier ecuación que tenga potencia impar debe tener una raíz real. Por tanto, una ecuación cúbica debe tener al menos una raíz real, a diferencia de una ecuación cuadrática donde ambas raíces pueden ser imaginarias cuando el discriminante es menor que cero.

5. ¿Puede una ecuación cúbica tener múltiples soluciones?

Sí, las ecuaciones cúbicas pueden tener múltiples soluciones, ya que una ecuación cúbica puede tener hasta tres raíces reales distintas.

generador de números aleatorios en c

6. ¿Qué quieres decir con grado de una ecuación?

La potencia máxima que posee la variable en una ecuación se llama grado de un polinomio.

7. ¿Cuál es la diferencia entre un polinomio y una ecuación?

Un polinomio es simplemente una ecuación algebraica en la que la potencia de la variable es un número entero no negativo. Este polinomio cuando se equipara (=) con un valor numérico u otro polinomio se llama ecuación.

8. ¿Cuál es el teorema del factor para ecuaciones cúbicas?

El teorema del factor establece que si r es una raíz (solución) de la ecuación cúbica ax³+ bx²+ cx + d = 0, entonces x – r es un factor de la ecuación.

9. ¿Qué pasa si no puedo encontrar soluciones exactas usando fórmulas?

Si encontrar soluciones exactas parece imposible, podemos usar métodos numéricos como los métodos iterativos (por ejemplo, el método de Newton) para aproximar las raíces de la ecuación.

Aprender más acerca de El método de Newton Raphson .