Dada una cadena, encuentre todas las formas de romper la cadena dada en forma de soporte. Encerrar cada subcadena dentro de un paréntesis.
atajos de Linux
Ejemplos:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Le recomendamos encarecidamente que minimice su navegador e intente esto usted mismo primero.
La idea es usar la recursión. Mantenemos dos parámetros: índice del siguiente carácter que se procesará y la cadena de salida hasta ahora. Comenzamos desde el índice del siguiente carácter para ser procesado de sustras de agregado formado por una cadena sin procesar a la cadena de salida y recurrir en la cadena restante hasta que procesemos toda la cadena. Usamos std :: substr para formar la cadena de salida. SubStr (POS N) Devuelve una subcadena de longitud n que comienza en la posición POS de la cadena actual.
A continuación, el diagrama muestra el árbol de recursión para la cadena de entrada 'ABC'. Cada nodo en el diagrama muestra una cadena procesada (marcada por verde) y una cadena sin procesar (marcada por rojo).
la cadena java está vacía
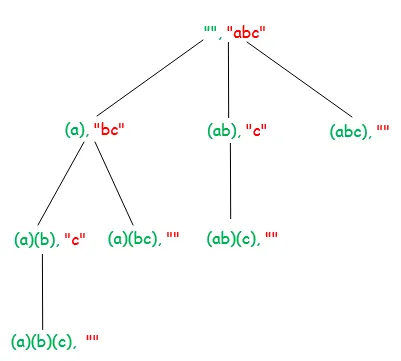
A continuación se muestra la implementación de la idea anterior
C++// C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include
// Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations(String str int index String out) { if (index == str.length()) System.out.println(out); for (int i = index; i < str.length(); i++) // append substring formed by str[index // i] to output string findCombinations(str i + 1 out + '(' + str.substring(index i+1) + ')' ); } // Driver Code public static void main (String[] args) { // input string String str = 'abcd'; findCombinations(str 0 ''); } } // Contributed by Pramod Kumar
# Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations(string index out): if index == len(string): print(out) for i in range(index len(string) 1): # append substring formed by str[index # i] to output string findCombinations(string i + 1 out + '(' + string[index:i + 1] + ')') # Driver Code if __name__ == '__main__': # input string string = 'abcd' findCombinations(string 0 '') # This code is contributed by # sanjeev2552
// C# program to find all combinations // of Non-overlapping substrings formed // from given string using System; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations(string str int index string @out) { if (index == str.Length) { Console.WriteLine(@out); } for (int i = index; i < str.Length; i++) { // append substring formed by // str[index i] to output string findCombinations( str i + 1 @out + '(' + str.Substring(index (i + 1) - index) + ')'); } } // Driver Code public static void Main(string[] args) { // input string string str = 'abcd'; findCombinations(str 0 ''); } } // This code is contributed by Shrikant13
// Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations(string index out) { if (index == string.length) { console.log(out); } for (let i = index; i < string.length; i++) { // append substring formed by str[index // i] to output string findCombinations(string i + 1 out + '(' + string.substring(index i + 1) + ')'); } } // Driver Code const string = 'abcd'; findCombinations(string 0 ''); // contributed by adityasharmadev01
Producción
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Complejidad del tiempo: O (N2)
Espacio auxiliar: O (N2)
lenguaje de computadora maravilloso
