Existen numerosas formas de evaluar el desempeño de un clasificador. En este artículo, presentamos la curva de recuperación de precisión y examinamos más a fondo la diferencia entre dos métodos populares de informes de rendimiento: curva de recuperación de precisión (PR) y Característica operativa del receptor (ROC) Curva. La curva ROC ya se analiza en el artículo . Entendamos brevemente qué es una curva de recuperación de precisión.
¿Qué es precisión y recuperación?
Precisión
- La proporción entre observaciones positivas pronosticadas correctamente y todas las positivas pronosticadas se conoce como precisión.
- Mide qué tan bien el modelo pronostica los resultados positivos.
- La fórmula de precisión es:
- La precisión tiene que ver con la calidad de las predicciones positivas. Una precisión alta indica que el modelo tiene una tasa baja de falsos positivos.
Recordar
- La relación entre las observaciones positivas predichas correctamente y el número total de observaciones positivas reales se conoce como recuerdo.
- Mide qué tan bien el modelo puede capturar cada instancia pertinente.
- La recuperación se calcula utilizando esta fórmula:
- La recuperación se refiere a la cantidad de instancias relevantes capturadas por el modelo. Una recuperación alta indica que el modelo tiene una tasa baja de falsos negativos.
En términos de interpretación empírica, una matriz de confusión que comprende cuatro términos esenciales es la herramienta más útil para comprender la precisión y el recuerdo:
- Verdadero positivo (TP): el número de instancias de clase positivas que se identifican con precisión
- Falso positivo (FP): el número de instancias de clases negativas que se identifican erróneamente como instancias de clases positivas se conoce como falso positivo (FP).
- Verdadero negativo (TN): el número de instancias de clase negativas que se identifican con precisión
- Falso Negativo (FN): Recuento de instancias de clase positivas que se clasifican erróneamente como instancias de clase negativas (Falso Negativo o FN)
Curva de recuperación de precisión (PR) en el aprendizaje automático
Precisión es la proporción de correcto clasificaciones positivas (verdaderos positivos) divididas por el número total de predicho clasificaciones positivas que se realizaron (verdadero positivo + falso positivo). Recordar es la proporción de correcto clasificaciones positivas (verdaderos positivos) divididas por el número total de realmente clasificaciones positivas (verdadero positivo + falso negativo).
Una curva PR es simplemente un gráfico con valores de precisión en el eje y y valores de recuperación en el eje x. En otras palabras, la curva PR contiene
java comparable
- Es importante tener en cuenta que la precisión también se denomina valor predictivo positivo (PPV).
- El retiro también se llama Sensibilidad, Tasa de aciertos o Tasa de verdaderos positivos (TPR).
La siguiente figura muestra una comparación de muestras de curvas PR y ROC. 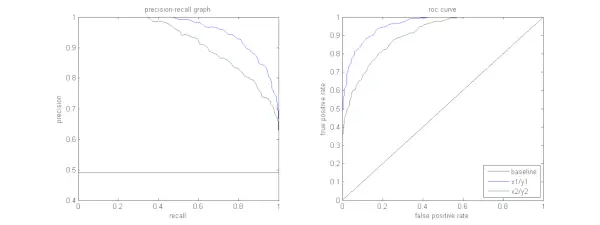
Interpretación de una curva de recuperación de precisión
Se desea que el algoritmo tenga alta precisión y alta recuperación. Sin embargo, la mayoría de los algoritmos de aprendizaje automático suelen implicar un equilibrio entre ambos. Una buena curva de relaciones públicas tiene mayor AUC (área bajo la curva) . En la figura anterior, el clasificador correspondiente a la línea azul tiene mejor rendimiento que el clasificador correspondiente a la línea verde. Es importante tener en cuenta que el clasificador que tiene un AUC más alto en el curva ROC siempre tendrá un AUC más alto en la curva PR también. Consideremos un algoritmo que clasifica si un documento pertenece o no a la categoría Noticias deportivas. Supongamos que hay 12 documentos, con las siguientes etiquetas de clase de salida del clasificador y de verdad fundamental (real).
| Identificación del documento | Verdad fundamental | Salida del clasificador |
|---|---|---|
| D1 | Deportes | Deportes |
| D2 | Deportes | Deportes |
| D3 | No deportes | Deportes |
| D4 | Deportes | No deportes |
| D5 | No deportes | No deportes |
| D6 | Deportes | No deportes |
| D7 | No deportes | Deportes |
| D8 | No deportes | No deportes |
| D9 | No deportes | No deportes |
| D10 | Deportes | Deportes |
| D11 | Deportes | Deportes |
| D12 | Deportes | No deportes |
Ahora, encontremos los valores de TP, TN, FP y FN.
Usemos un ejemplo que involucre documentos clasificados como Deportes o No deportes para explicar mejor las definiciones de Verdaderos Positivos (TP), Verdaderos Negativos (TN), Falsos Positivos (FP) y Falsos Negativos (FN) en el contexto de la clasificación:
Verdaderos Positivos (TP): Documentos que estaban categorizados con precisión como Deportes y que en realidad trataban sobre deportes. Los documentos D1, D2, D10 y D11 en este escenario son instancias de TP.
Verdaderos negativos (TN): Los Verdaderos Negativos son aquellos casos en los que el documento fue correctamente etiquetado como No deportivo aunque no tuviera nada que ver con deportes. En este caso, TN se demuestra en los documentos D5, D8 y D9.
Falsos positivos (FP): Documentos que fueron categorizados erróneamente como Deportes aunque no tenían nada que ver con deportes. A continuación se muestran algunos ejemplos de FP, documentos D3 y D7.
Falsos negativos (FN): Ejemplos de documentos que fueron etiquetados erróneamente como No deportivos, pero que en realidad trataban de deportes. Los documentos D4, D6 y D12 en este caso son ejemplos de FN.
Teniendo en cuenta estos recuentos: Ciudad =4, Tennesse =3, FP =2, FN =3
Finalmente, la precisión y la recuperación se calculan de la siguiente manera:
Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}
Recall = frac{TP}{TP+FN} = frac{4}{7} De ello se deduce que la recuperación es 4/7 cuando la precisión es 2/3. Dicho de otra manera, de todos los casos que se preveía que serían positivos, dos tercios se clasificaron con precisión (precisión), y de todos los casos que fueron realmente positivos, el modelo pudo capturar cuatro séptimos de ellos (recuerdo).
Al establecer diferentes umbrales, obtenemos múltiples pares de recuperación de precisión. Al trazar varios de estos pares P-R con cualquier valor entre 0 y 1, obtenemos una curva PR.
¿Necesita una curva PR cuando existe la curva ROC?
La curva PR es particularmente útil para informar resultados de recuperación de información.
La recuperación de información implica buscar en un conjunto de documentos para encontrar aquellos que sean relevantes para la consulta de un usuario en particular. Por ejemplo, supongamos que el usuario ingresa una consulta de búsqueda Elefantes rosados. El motor de búsqueda hojea millones de documentos (utilizando algunos algoritmos optimizados) para recuperar un puñado de documentos relevantes. Por lo tanto, podemos asumir con seguridad que el no. de documentos relevantes será mucho menor en comparación con el no. de documentos no relevantes.
En este escenario,
- TP = No. de documentos recuperados que son relevantes (buenos resultados).
- FP = Número de documentos recuperados que no son relevantes (resultados de búsqueda falsos).
- TN = No. de documentos no recuperados que no son relevantes.
- FN = Número de documentos no recuperados que son relevantes (buenos documentos que nos perdimos).
La curva ROC es un gráfico que contiene Recall = TPR =
Además, FPR no nos ayuda a evaluar bien un sistema de recuperación porque queremos centrarnos más en los documentos recuperados y no en los no recuperados. La curva PR ayuda a resolver este problema. La curva PR tiene el valor de recuperación (TPR) en el eje x y la precisión =
¿Cuándo utilizar curvas ROC frente a curvas de recuperación de precisión?
República de China Las curvas (característica operativa del receptor) son adecuadas cuando la distribución de clases está equilibrada y los falsos positivos y falsos negativos tienen consecuencias similares. Representan el equilibrio entre sensibilidad y especificidad. Por el contrario, las curvas Precision-Recall son preferibles cuando se trata de conjuntos de datos desequilibrados, ya que se centran en el rendimiento positivo de la predicción de clases.
Precision-Recall proporciona información sobre la capacidad del modelo para clasificar correctamente instancias positivas. La elección entre ROC y Precision-Recall depende de las necesidades específicas del problema, lo que enfatiza la importancia de comprender la distribución de datos y las consecuencias de los diferentes tipos de errores.
Implementación de código básico para la curva de recuperación de precisión
Importación de bibliotecas necesarias
Estas líneas de código importan el Bibliotecas de Python y módulos necesarios para generar una curva de recuperación de precisión con kit de ciencia-aprender y visualizar los resultados con Matplotlib . Matplotlib es una biblioteca de trazado de Python popular y pyplot proporciona una interfaz sencilla para crear varios tipos de trazados y cuadros. Regresión logística es un algoritmo de clasificación popular para tareas de clasificación binaria y multiclase. La curva de recuperación de precisión y el AUC son métricas de evaluación populares para clasificación binaria problemas, particularmente cuando se trata de conjuntos de datos desequilibrados.
Python3 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc> Conjunto de datos utilizado
Este código genera un conjunto de datos sintéticos para un problema de clasificación binaria utilizando la función 'make_classification' de sci-kit-learn.
mapa vs conjuntoPython3
# Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)> División de entrenamiento y prueba
El tren_prueba_split La función en scikit-learn se utiliza en este fragmento de código para dividir el conjunto de datos sintéticos generado previamente (X e y) en conjuntos de entrenamiento y prueba. Esta división es un paso crítico en la evaluación de modelos de aprendizaje automático. El modelo se entrenará con los datos de X_train e y_train antes de probarlo con los datos de X_test e y_test para ver qué tan bien se desempeña en muestras invisibles. La función train_test_split separa los conjuntos de entrenamiento y prueba, asegurando que el rendimiento del modelo refleje su generalización a datos nuevos, nunca antes vistos.
Python3 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)> Construcción del modelo
Aquí utilizamos la regresión logística para entrenar el modelo en el conjunto de datos de entrenamiento. La regresión logística, un algoritmo popular para la clasificación binaria, se implementa mediante la clase LogisticRegression de sci-kit-learn.
Python3 # Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)> Predicción del modelo
Estos cálculos generalmente brindan valores de precisión y recuperación para varios umbrales de decisión, que se pueden usar para dibujar una curva de recuperación de precisión o examinar la importancia relativa de la precisión y la recuperación en varios momentos. Y calculando el Área bajo la curva (AUC) para la curva de recuperación de precisión.
Python3 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)> Trazar la curva PR
Este bloque de código proporciona un método estándar para visualizar la curva de recuperación de precisión y le permite evaluar la compensación entre precisión y recuperación en varios umbrales de decisión. El rendimiento general del modelo en la curva de recuperación de precisión se resume en la puntuación AUC que se muestra en la leyenda.
Python3 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()> Producción :

Curva de recuperación de precisión
Preguntas frecuentes (FAQ)
P. ¿Qué es la precisión?
La relación entre las observaciones positivas predichas con precisión y el número total de positivas predichas se conoce como precisión. Mide qué tan bien el modelo predice los resultados positivos. La siguiente es la fórmula de precisión:
Precision = frac{True Positives}{True Positives + False Positives}
P. ¿Qué es el retiro?
La recuperación es la relación entre las observaciones positivas predichas correctamente y el número total de positivas reales. También se conoce como sensibilidad o tasa de verdaderos positivos. Evalúa qué tan bien el modelo puede capturar cada instancia pertinente. La recuperación se calcula utilizando la siguiente fórmula:
Precision = frac{True Positives}{True Positives + False Negatives}
P. ¿Por qué necesitamos precisión y recuerdo?
Para evaluar el desempeño de un clasificador en problemas de clasificación binaria y multiclase, se utilizan dos métricas de evaluación: precisión y recuperación. La exactitud de la predicción positiva se mide mediante la precisión y la integridad de la predicción positiva se mide mediante el recuerdo.
P. ¿Cuál es la compensación entre retiro y precisión?
El recuerdo y la precisión son frecuentemente compensaciones. La recuperación puede verse afectada a medida que aumenta la precisión y viceversa. Al cambiar la barra para identificar un caso positivo, se puede gestionar esta compensación. Por el contrario, un umbral más bajo da como resultado una menor recuperación pero una mayor precisión. La decisión entre recuperación y precisión se basa en los detalles del problema dado.
P. ¿Qué es la puntuación F1 y cómo se relaciona con la precisión y la recuperación?
La media armónica de recuerdo y precisión se conoce como puntuación F1. Ofrece una medición justa que tiene en cuenta tanto los falsos positivos como los falsos negativos. La puntuación F1 se calcula mediante la siguiente fórmula:
F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall} La puntuación F1 es especialmente útil cuando la precisión y la recuperación están desequilibradas y se desea un equilibrio entre ambas.
