Regresión logística es un algoritmo de aprendizaje automático supervisado usado para tareas de clasificación donde el objetivo es predecir la probabilidad de que una instancia pertenezca o no a una clase determinada. La regresión logística es un algoritmo estadístico que analiza la relación entre dos factores de datos. El artículo explora los fundamentos de la regresión logística, sus tipos e implementaciones.
Tabla de contenidos
- ¿Qué es la regresión logística?
- Función logística – Función sigmoidea
- Tipos de regresión logística
- Supuestos de regresión logística
- ¿Cómo funciona la regresión logística?
- Implementación de código para regresión logística
- Compensación entre precisión y recuperación en el establecimiento de umbrales de regresión logística
- ¿Cómo evaluar el modelo de regresión logística?
- Diferencias entre regresión lineal y logística
¿Qué es la regresión logística?
La regresión logística se utiliza para binario. clasificación donde usamos función sigmoidea , que toma entradas como variables independientes y produce un valor de probabilidad entre 0 y 1.
Por ejemplo, tenemos dos clases, Clase 0 y Clase 1, si el valor de la función logística para una entrada es mayor que 0,5 (valor umbral), entonces pertenece a la Clase 1; de lo contrario, pertenece a la Clase 0. Se conoce como regresión porque es la extensión de regresión lineal pero se utiliza principalmente para problemas de clasificación.
Puntos clave:
- La regresión logística predice la salida de una variable dependiente categórica. Por lo tanto, el resultado debe ser un valor categórico o discreto.
- Puede ser Sí o No, 0 o 1, Verdadero o Falso, etc. pero en lugar de dar el valor exacto como 0 y 1, da los valores probabilísticos que se encuentran entre 0 y 1.
- En la regresión logística, en lugar de ajustar una línea de regresión, ajustamos una función logística en forma de S, que predice dos valores máximos (0 o 1).
Función logística – Función sigmoidea
- La función sigmoidea es una función matemática que se utiliza para asignar los valores predichos a probabilidades.
- Asigna cualquier valor real a otro valor dentro de un rango de 0 y 1. El valor de la regresión logística debe estar entre 0 y 1, que no puede ir más allá de este límite, por lo que forma una curva como la forma S.
- La curva en forma de S se llama función sigmoidea o función logística.
- En la regresión logística, utilizamos el concepto de valor umbral, que define la probabilidad de 0 o 1. Por ejemplo, los valores por encima del valor umbral tienden a 1 y un valor por debajo del valor umbral tiende a 0.
Tipos de regresión logística
Según las categorías, la regresión logística se puede clasificar en tres tipos:
- Binomio: En la regresión logística binomial, solo puede haber dos tipos posibles de variables dependientes, como 0 o 1, Pasa o Falla, etc.
- Multinomial: En la regresión logística multinomial, puede haber 3 o más tipos desordenados posibles de la variable dependiente, como gato, perro u oveja.
- Ordinal: En la regresión logística ordinal, puede haber 3 o más tipos ordenados posibles de variables dependientes, como baja, media o alta.
Supuestos de regresión logística
Exploraremos los supuestos de la regresión logística, ya que comprender estos supuestos es importante para garantizar que estamos utilizando la aplicación adecuada del modelo. Los supuestos incluyen:
- Observaciones independientes: cada observación es independiente de la otra. lo que significa que no hay correlación entre ninguna variable de entrada.
- Variables dependientes binarias: se asume que la variable dependiente debe ser binaria o dicotómica, lo que significa que solo puede tomar dos valores. Para más de dos categorías se utilizan funciones SoftMax.
- Relación de linealidad entre variables independientes y probabilidades logarítmicas: la relación entre las variables independientes y las probabilidades logarítmicas de la variable dependiente debe ser lineal.
- Sin valores atípicos: no debería haber valores atípicos en el conjunto de datos.
- Tamaño de muestra grande: el tamaño de la muestra es suficientemente grande
Terminologías involucradas en la regresión logística
A continuación se muestran algunos términos comunes involucrados en la regresión logística:
- Variables independientes: Las características de entrada o factores predictores aplicados a las predicciones de la variable dependiente.
- Variable dependiente: La variable objetivo en un modelo de regresión logística, que estamos tratando de predecir.
- Función logística: La fórmula utilizada para representar cómo se relacionan entre sí las variables independientes y dependientes. La función logística transforma las variables de entrada en un valor de probabilidad entre 0 y 1, que representa la probabilidad de que la variable dependiente sea 1 o 0.
- Impares: Es la relación entre algo que ocurre y algo que no ocurre. es diferente de la probabilidad ya que la probabilidad es la relación entre algo que ocurre y todo lo que posiblemente podría ocurrir.
- Probabilidades de registro: El logaritmo de probabilidades, también conocido como función logit, es el logaritmo natural de las probabilidades. En la regresión logística, las probabilidades logarítmicas de la variable dependiente se modelan como una combinación lineal de las variables independientes y la intersección.
- Coeficiente: Los parámetros estimados del modelo de regresión logística muestran cómo se relacionan entre sí las variables independientes y dependientes.
- Interceptar: Un término constante en el modelo de regresión logística, que representa las probabilidades logarítmicas cuando todas las variables independientes son iguales a cero.
- Estimación de máxima verosimilitud : El método utilizado para estimar los coeficientes del modelo de regresión logística, que maximiza la probabilidad de observar los datos dado el modelo.
¿Cómo funciona la regresión logística?
El modelo de regresión logística transforma la regresión lineal Función de salida de valor continuo en salida de valor categórico utilizando una función sigmoidea, que asigna cualquier conjunto de variables independientes de valor real ingresado a un valor entre 0 y 1. Esta función se conoce como función logística.
shreya ghoshal
Sean las características de entrada independientes:
y la variable dependiente es Y y tiene solo valor binario, es decir, 0 o 1.
luego, aplique la función multilineal a las variables de entrada X.
Aquí
todo lo que discutimos anteriormente es el regresión lineal .
Función sigmoidea
Ahora usamos el función sigmoidea donde la entrada será z y encontramos la probabilidad entre 0 y 1. es decir, y predicha.
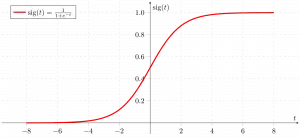
función sigmoidea
Como se muestra arriba, la función figura sigmoidea convierte los datos de la variable continua en probabilidad es decir, entre 0 y 1.
sigma(z) tiende hacia 1 comoz ightarrowinfty sigma(z) tiende hacia 0 comoz ightarrow-infty sigma(z) siempre está limitado entre 0 y 1
donde la probabilidad de ser una clase se puede medir como:
Ecuación de regresión logística
Lo impar es la proporción entre algo que ocurre y algo que no ocurre. es diferente de la probabilidad ya que la probabilidad es la relación entre algo que ocurre y todo lo que posiblemente podría ocurrir. tan extraño será:
Aplicando registro natural en impar. entonces el registro impar será:
entonces la ecuación de regresión logística final será:
Función de probabilidad para la regresión logística
Las probabilidades previstas serán:
- para y=1 Las probabilidades predichas serán: p(X;b,w) = p(x)
- para y = 0 Las probabilidades predichas serán: 1-p(X;b,w) = 1-p(x)
Tomando troncos naturales por ambos lados.
patrones de programación java
Gradiente de la función logarítmica de verosimilitud
Para encontrar las estimaciones de máxima verosimilitud, diferenciamos w.r.t w,
Implementación de código para regresión logística
Regresión logística binomial:
La variable objetivo puede tener solo 2 tipos posibles: 0 o 1, que puede representar ganar versus perder, pasar versus fallar, muerto versus vivo, etc., en este caso, se utilizan funciones sigmoideas, que ya se discutieron anteriormente.
Importación de bibliotecas necesarias según los requisitos del modelo. Este código Python muestra cómo utilizar el conjunto de datos de cáncer de mama para implementar un modelo de regresión logística para la clasificación.
Python3 # import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X, y = load_breast_cancer(return_X_y=True) # split the train and test dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23) # LogisticRegression clf = LogisticRegression(random_state=0) clf.fit(X_train, y_train) # Prediction y_pred = clf.predict(X_test) acc = accuracy_score(y_test, y_pred) print('Logistic Regression model accuracy (in %):', acc*100)> Producción :
Precisión del modelo de regresión logística (en %): 95,6140350877193
Regresión logística multinomial:
La variable objetivo puede tener 3 o más tipos posibles que no están ordenados (es decir, los tipos no tienen importancia cuantitativa), como enfermedad A, enfermedad B y enfermedad C.
En este caso, la función softmax se utiliza en lugar de la función sigmoidea. función softmax para las clases K será:
Aquí, k representa el número de elementos en el vector z, e i, j itera sobre todos los elementos del vector.
Entonces la probabilidad para la clase c será:
En la regresión logística multinomial, la variable de salida puede tener más de dos posibles salidas discretas . Considere el conjunto de datos de dígitos.
Python3 from sklearn.model_selection import train_test_split from sklearn import datasets, linear_model, metrics # load the digit dataset digits = datasets.load_digits() # defining feature matrix(X) and response vector(y) X = digits.data y = digits.target # splitting X and y into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) # create logistic regression object reg = linear_model.LogisticRegression() # train the model using the training sets reg.fit(X_train, y_train) # making predictions on the testing set y_pred = reg.predict(X_test) # comparing actual response values (y_test) # with predicted response values (y_pred) print('Logistic Regression model accuracy(in %):', metrics.accuracy_score(y_test, y_pred)*100)> Producción:
Precisión del modelo de regresión logística (en %): 96,52294853963839
¿Cómo evaluar el modelo de regresión logística?
Podemos evaluar el modelo de regresión logística utilizando las siguientes métricas:
- Exactitud: Exactitud proporciona la proporción de instancias clasificadas correctamente.
Accuracy = frac{True , Positives + True , Negatives}{Total}
- Precisión: Precisión se centra en la precisión de las predicciones positivas.
Precision = frac{True , Positives }{True, Positives + False , Positives}
- Recuperación (sensibilidad o tasa de verdaderos positivos): Recordar Mide la proporción de casos positivos pronosticados correctamente entre todos los casos positivos reales.
Recall = frac{ True , Positives}{True, Positives + False , Negatives}
- Puntuación F1: puntuación F1 es la media armónica de precisión y recuperación.
F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}
- Área bajo la curva característica operativa del receptor (AUC-ROC): La curva ROC traza la tasa de verdaderos positivos frente a la tasa de falsos positivos en varios umbrales. AUC-ROC Mide el área bajo esta curva, proporcionando una medida agregada del desempeño de un modelo a través de diferentes umbrales de clasificación.
- Área bajo la curva de recuperación de precisión (AUC-PR): Similar a las AUC-ROC, AUC-PR Mide el área bajo la curva de recuperación de precisión, proporcionando un resumen del rendimiento de un modelo en diferentes compensaciones de recuperación de precisión.
Compensación entre precisión y recuperación en el establecimiento de umbrales de regresión logística
La regresión logística se convierte en una técnica de clasificación sólo cuando se introduce en escena un umbral de decisión. El establecimiento del valor umbral es un aspecto muy importante de la regresión logística y depende del problema de clasificación en sí.
La decisión sobre el valor del valor umbral se ve afectada en gran medida por los valores de precisión y recuperación. Idealmente, queremos que tanto la precisión como la recuperación sean 1, pero rara vez es así.
En el caso de un Compensación de precisión-recuperación , utilizamos los siguientes argumentos para decidir sobre el umbral:
- Baja precisión/alta recuperación: En aplicaciones donde queremos reducir la cantidad de falsos negativos sin reducir necesariamente la cantidad de falsos positivos, elegimos un valor de decisión que tiene un valor bajo de Precisión o un valor alto de Recuperación. Por ejemplo, en una aplicación de diagnóstico de cáncer, no queremos que ningún paciente afectado sea clasificado como no afectado sin prestar mucha atención a si al paciente se le diagnostica cáncer erróneamente. Esto se debe a que la ausencia de cáncer puede detectarse mediante otras enfermedades médicas, pero la presencia de la enfermedad no puede detectarse en un candidato ya rechazado.
- Alta precisión/baja recuperación: En aplicaciones donde queremos reducir la cantidad de falsos positivos sin reducir necesariamente la cantidad de falsos negativos, elegimos un valor de decisión que tiene un valor alto de Precisión o un valor bajo de Recuperación. Por ejemplo, si clasificamos a los clientes según reaccionarán positiva o negativamente a un anuncio personalizado, queremos estar absolutamente seguros de que el cliente reaccionará positivamente al anuncio porque, de lo contrario, una reacción negativa puede provocar una pérdida de ventas potenciales del producto. cliente.
Diferencias entre regresión lineal y logística
La diferencia entre regresión lineal y regresión logística es que el resultado de la regresión lineal es el valor continuo que puede ser cualquier cosa, mientras que la regresión logística predice la probabilidad de que una instancia pertenezca a una clase determinada o no.
Regresión lineal | Regresión logística |
|---|---|
La regresión lineal se utiliza para predecir la variable dependiente continua utilizando un conjunto determinado de variables independientes. | La regresión logística se utiliza para predecir la variable dependiente categórica utilizando un conjunto determinado de variables independientes. |
La regresión lineal se utiliza para resolver problemas de regresión. | Se utiliza para resolver problemas de clasificación. |
En esto predecimos el valor de las variables continuas. | En esto predecimos valores de variables categóricas. |
En esto encontramos la línea de mejor ajuste. | En esto encontramos la curva S. |
El método de estimación de mínimos cuadrados se utiliza para estimar la precisión. | El método de estimación de máxima verosimilitud se utiliza para estimar la precisión. |
La salida debe ser un valor continuo, como precio, edad, etc. | La salida debe ser un valor categórico como 0 o 1, Sí o no, etc. |
Requería una relación lineal entre variables dependientes e independientes. | No requirió relación lineal. |
Puede haber colinealidad entre las variables independientes. | No debe haber colinealidad entre variables independientes. |
Regresión logística: preguntas frecuentes (FAQ)
¿Qué es la regresión logística en el aprendizaje automático?
La regresión logística es un método estadístico para desarrollar modelos de aprendizaje automático con variables dependientes binarias, es decir, binarias. La regresión logística es una técnica estadística utilizada para describir datos y la relación entre una variable dependiente y una o más variables independientes.
¿Cuáles son los tres tipos de regresión logística?
La regresión logística se clasifica en tres tipos: binaria, multinomial y ordinal. Se diferencian tanto en la ejecución como en la teoría. La regresión binaria se ocupa de dos resultados posibles: sí o no. La regresión logística multinomial se utiliza cuando hay tres o más valores.
programa en java
¿Por qué se utiliza la regresión logística para el problema de clasificación?
La regresión logística es más fácil de implementar, interpretar y entrenar. Clasifica registros desconocidos muy rápidamente. Cuando el conjunto de datos es linealmente separable, funciona bien. Los coeficientes del modelo pueden interpretarse como indicadores de la importancia de una característica.
¿Qué distingue la regresión logística de la regresión lineal?
Mientras que la regresión lineal se utiliza para predecir resultados continuos, la regresión logística se utiliza para predecir la probabilidad de que una observación caiga en una categoría específica. La regresión logística emplea una función logística en forma de S para mapear valores predichos entre 0 y 1.
¿Qué papel juega la función logística en la regresión logística?
La regresión logística se basa en la función logística para convertir el resultado en una puntuación de probabilidad. Esta puntuación representa la probabilidad de que una observación pertenezca a una clase particular. La curva en forma de S ayuda a establecer umbrales y categorizar datos en resultados binarios.
