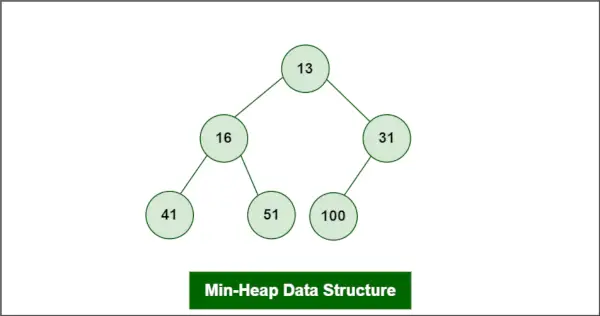
A montón mínimo se define como un tipo de La estructura de datos del montón es un tipo de árbol binario que se usa comúnmente en informática para diversos fines, incluida la clasificación, búsqueda y organización de datos.
Introducción a Min-Heap: tutoriales de algoritmos y estructura de datos
Propósito y casos de uso de Min-Heap:
para bucle en c
- Implementación de cola de prioridad: Uno de los usos principales de la estructura de datos del montón es implementar colas de prioridad.
- Algoritmo de Dijkstra : El algoritmo de Dijkstra es un algoritmo de camino más corto que encuentra el camino más corto entre dos nodos en un gráfico. Se puede utilizar un montón mínimo para realizar un seguimiento de los nodos no visitados con la distancia más pequeña desde el nodo de origen.
- Clasificación: Se puede utilizar un montón mínimo como algoritmo de clasificación para ordenar de manera eficiente una colección de elementos en orden ascendente.
- Hallazgo mediano: Se puede utilizar un montón mínimo para encontrar de manera eficiente la mediana de un flujo de números. Podemos usar un montón mínimo para almacenar la mitad más grande de los números y un montón máximo para almacenar la mitad más pequeña. La mediana será la raíz del montón mínimo.
Estructura de datos Min-Heap en diferentes idiomas:
1. Montón mínimo en C++
Se puede implementar un montón mínimo usando el cola_prioridad contenedor de la Biblioteca de plantillas estándar (STL). El cola_prioridad contenedor es un tipo de adaptador de contenedor que proporciona una forma de almacenar elementos en una estructura de datos similar a una cola en la que cada elemento tiene una prioridad asociada.
Sintaxis :
C++ priority_queue < int, vector , mayor que > minH;>
2. Montón mínimo en Java
En Java, se puede implementar un montón mínimo usando el Cola de prioridad clase de paquete java.util . La clase PriorityQueue es una cola de prioridad que proporciona una manera de almacenar elementos en una estructura de datos similar a una cola en la que cada elemento tiene una prioridad asociada.
Sintaxis :
Java PriorityQueue minHeap = nueva PriorityQueue ();>
3. Montón mínimo en Python
En Python, se puede implementar un montón mínimo usando el montónq módulo, que proporciona funciones para implementar montones. Específicamente, el montónq El módulo proporciona una manera de crear y manipular estructuras de datos de montón.
Sintaxis:
Pitón heap = [] heapify(heap)>
4. Min-Heap en C#
En C#, se puede implementar un montón mínimo usando la clase PriorityQueue del System.Collections.Espacio de nombres genérico . La clase PriorityQueue es una cola de prioridad que proporciona una manera de almacenar elementos en una estructura de datos similar a una cola en la que cada elemento tiene una prioridad asociada.
Sintaxis:
C# var minHeap = new PriorityQueue ();>
5. Montón mínimo en JavaScript
Un montón mínimo es un árbol binario donde cada nodo tiene un valor menor o igual que sus hijos. En JavaScript, puede implementar un montón mínimo usando una matriz, donde el primer elemento representa el nodo raíz y los hijos de un nodo en el índice. i están ubicados en índices 2i+1 y 2i+2.
Sintaxis:
javascript const minHeap = new MinHeap();>
Diferencia entre montón mínimo y montón máximo:
|
| Montón mínimo | Montón máximo |
|---|---|---|
| 1. | En un Min-Heap, la clave presente en el nodo raíz debe ser menor o igual que entre las claves presentes en todos sus hijos. patrones de diseño en java | En un Max-Heap, la clave presente en el nodo raíz debe ser mayor o igual que entre las claves presentes en todos sus hijos. |
| 2. | En un Min-Heap, el elemento clave mínimo está presente en la raíz. | En un Max-Heap, el elemento clave máximo está presente en la raíz. |
| 3. | Un Min-Heap utiliza la prioridad ascendente. | Un Max-Heap utiliza la prioridad descendente. |
| 4. | En la construcción de un Min-Heap, el elemento más pequeño tiene prioridad. | En la construcción de un Max-Heap, el elemento más grande tiene prioridad. |
| 5. | En un Min-Heap, el elemento más pequeño es el primero que se extrae del montón. | En un Max-Heap, el elemento más grande es el primero que se extrae del montón. |
Implementación interna de la estructura de datos Min-Heap:
A El montón mínimo normalmente se representa como una matriz .
- El elemento raíz estará en Llegada[0] .
- Para cualquier i-ésimo nodo Arr[yo] :
- Arr[(i -1) / 2] devuelve su nodo padre.
- Arr[(2 * i) + 1] devuelve su nodo hijo izquierdo.
- Arr[(2 * i) + 2] devuelve su nodo hijo derecho.
La implementación interna del Min-Heap requiere 3 pasos principales:
identificadores válidos de java
- Inserción : Para insertar un elemento en el montón mínimo, primero agregamos el elemento al final de la matriz y luego ajustamos la propiedad del montón intercambiando repetidamente el elemento con su padre hasta que esté en la posición correcta.
- Supresión : Para eliminar el elemento mínimo del montón mínimo, primero intercambiamos el nodo raíz con el último elemento de la matriz, eliminamos el último elemento y luego ajustamos la propiedad del montón intercambiando repetidamente el elemento con su hijo más pequeño hasta que esté en el montón. posicion correcta.
- amontonar : Se puede utilizar una operación de almacenamiento dinámico para crear un almacenamiento dinámico mínimo a partir de una matriz sin clasificar.
Operaciones sobre la estructura de datos Min-heap y su implementación:
A continuación se muestran algunas operaciones comunes que se pueden realizar en una estructura de datos del montón,
1. Inserción en estructura de datos Min-Heap :
Los elementos se pueden insertar en el montón siguiendo un enfoque similar al descrito anteriormente para su eliminación. La idea es:
- La operación de inserción en un montón mínimo implica los siguientes pasos:
- Agregue el nuevo elemento al final del montón, en la siguiente posición disponible en el último nivel del árbol.
- Compare el nuevo elemento con su padre. Si el padre es mayor que el nuevo elemento, cámbielos.
- Repita el paso 2 hasta que el padre sea menor o igual que el nuevo elemento, o hasta que el nuevo elemento llegue a la raíz del árbol.
- El nuevo elemento ahora está en su posición correcta en el montón mínimo y se cumple la propiedad del montón.
Ilustración:
Supongamos que el montón es un montón mínimo como:
Inserción en Min-Heap
Implementación de la operación de inserción en Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Agrega el nuevo elemento al final del montón heap.push_back(value); // Obtener el índice del último elemento int index = heap.size() - 1; // Compara el nuevo elemento con su padre e intercambia si // es necesario while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Sube en el árbol hasta el padre del // elemento actual index = (index - 1) / 2; } } // Función principal para probar la función insert_min_heap int main() { vector montón; valores int[] = {10, 7, 11, 5, 4, 13}; int n = tamaño de (valores) / tamaño de (valores [0]); para (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && montón[(índice - 1) / 2]> montón[índice]) { swap(montón, índice, (índice - 1) / 2); // Sube en el árbol hasta el padre del // elemento actual index = (index - 1) / 2; } } // Función para intercambiar dos elementos en una matriz public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arreglo[i] = arreglo[j]; arreglo[j] = temperatura; } // Función principal para probar la función insertMinHeap public static void main(String[] args) { int[] heap = new int[6]; valores int[] = {10, 7, 11, 5, 4, 13}; tamaño entero = 0; para (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 y montón[(índice - 1) // 2]> montón[índice]: montón[índice], montón[(índice - 1) // 2] = montón[(índice - 1) // 2], montón[ index] # Sube por el árbol hasta el elemento principal del elemento actual index = (index - 1) // 2 montón = [] valores = [10, 7, 11, 5, 4, 13] para el valor en valores: insert_min_heap( montón, valor) print(f'Insertado {valor} en el montón mínimo: {montón}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List montón, int valor) { // Agrega el nuevo elemento al final del montón heap.Add(value); // Obtener el índice del último elemento int index = heap.Count - 1; // Compara el nuevo elemento con su padre e intercambia // si es necesario while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; montón[índice] = montón[(índice - 1) / 2]; montón[(índice - 1) / 2] = temporal; // Sube en el árbol hasta el padre del // elemento actual index = (index - 1) / 2; } } // Función principal para probar la función InsertMinHeap public static void Main() { Lista montón = nueva lista (); valores int[] = {10, 7, 11, 5, 4, 13}; foreach(valor int en valores) { InsertMinHeap(montón, valor); Console.Write('Insertado ' + valor + ' en el montón mínimo: '); foreach(elemento int en el montón) { Console.Write(elemento + ' '); } Consola.WriteLine(); } } }> JavaScript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && montón[índice padre]> montón[índice]) { [montón[índice], montón[índice padre]] = [montón[índice padre], montón[índice]]; índice = índicepadre; parentIndex = Math.floor((índice - 1) / 2); } } // Ejemplo de uso const heap = []; valores constantes = [10, 7, 11, 5, 4, 13]; for (valor constante de los valores) { insertMinHeap(montón, valor); console.log(`Se insertó ${value} en el montón mínimo: ${heap}`); }> Producción
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Complejidad del tiempo: O(log(n)) ( donde n es el número de elementos en el montón )
Espacio Auxiliar: En)
2. Eliminación en la estructura de datos Min-Heap :
Eliminando el elemento más pequeño (la raíz) del montón mínimo. La raíz se reemplaza por el último elemento del montón y luego la propiedad del montón se restaura intercambiando la nueva raíz con su hijo más pequeño hasta que el padre sea más pequeño que ambos hijos o hasta que la nueva raíz alcance un nodo hoja.
- Reemplace la raíz o elemento que se eliminará con el último elemento.
- Elimina el último elemento del montón.
- Dado que el último elemento ahora se coloca en la posición del nodo raíz. Por lo tanto, es posible que no siga la propiedad del montón. Por lo tanto, amontone el último nodo colocado en la posición de la raíz.
Ilustración :
Supongamos que el montón es un montón mínimo como:
Estructura de datos del montón mínimo
El elemento a eliminar es root, es decir 13.
Proceso :
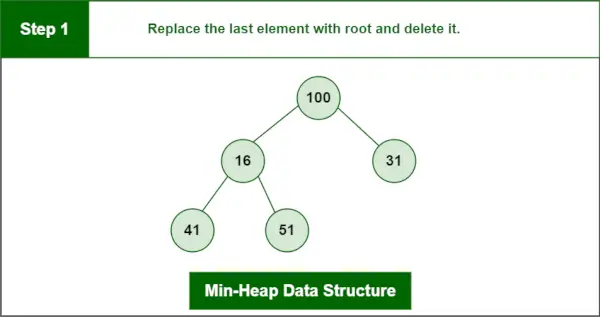
El último elemento es 100.
Paso 1: Reemplace el último elemento con raíz y elimínelo.
Estructura de datos del montón mínimo
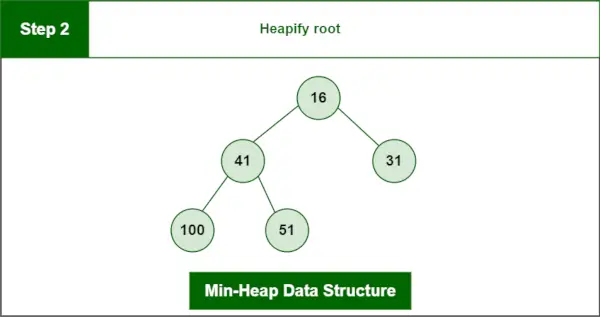
programa matricial en lenguaje cPaso 2 : Amontonar la raíz.
Montón final:
Estructura de datos del montón mínimo
Implementación de la operación de eliminación en Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Agrega el nuevo elemento al final del montón heap.push_back(value); // Obtener el índice del último elemento int index = heap.size() - 1; // Compara el nuevo elemento con su padre e intercambia si // es necesario while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Sube en el árbol hasta el padre del // elemento actual index = (index - 1) / 2; } } // Función para eliminar un nodo del min-heap void delete_min_heap(vector & heap, int value) { // Encuentra el índice del elemento que se va a eliminar int index = -1; para (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector montón; valores int[] = {13, 16, 31, 41, 51, 100}; int n = tamaño de (valores) / tamaño de (valores [0]); para (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List montón, int valor) { // Agrega el nuevo elemento al final del montón heap.add(value); // Obtener el índice del último elemento int index = heap.size() - 1; // Compara el nuevo elemento con su padre e intercambia // si es necesario while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (índice - 1) / 2); // Sube en el árbol hasta el padre del // elemento actual index = (index - 1) / 2; } } // Función para eliminar un nodo del min-heap public static void deleteMinHeap(List montón, int valor) { // Encuentra el índice del elemento que se va a eliminar int index = -1; para (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List montón = nueva ArrayList (); valores int[] = {13, 16, 31, 41, 51, 100}; int n = valores.longitud; para (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 y montón[(índice - 1) // 2]> montón[índice]: montón[índice], montón[(índice - 1) // 2] = montón[(índice - 1) // 2], montón[ índice] índice = (índice - 1) // 2 def eliminar_min_heap(montón, valor): índice = -1 para i en rango(len(montón)): si montón[i] == valor: índice = i rompo si índice == -1: devuelve montón[índice] = montón[-1] montón.pop() mientras que Verdadero: left_child = 2 * índice + 1 right_child = 2 * índice + 2 más pequeño = índice si left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List montón = nueva lista (); public void Insertar(valor int) { montón.Agregar(valor); int índice = montón.Count - 1; while (índice> 0 && montón[(índice - 1) / 2]> montón[índice]) { Intercambiar(índice, (índice - 1) / 2); índice = (índice - 1) / 2; } } public void Eliminar (valor int) { int índice = montón.IndexOf (valor); if (índice == -1) { retorno; } montón[índice] = montón[montón.Count - 1]; montón.RemoveAt(montón.Count - 1); mientras (verdadero) { int leftChild = 2 * índice + 1; int niñoderecho = 2 * índice + 2; int más pequeño = índice; si (izquierdaNiño< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> JavaScript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && montón[flr]> montón[índice]; flr = Math.floor((índice - 1) / 2)) { [montón[índice], montón[flr]] = [montón[flr], montón[índice], ]; // Sube en el árbol hasta el elemento principal del elemento actual index = Math.floor((index - 1) / 2); } } function eliminarMinHeap(heap, value) { // Encuentra el índice del elemento que se va a eliminar let index = -1; para (sea i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Producción
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Complejidad del tiempo : O(log n) donde n es el número de elementos del montón
Espacio Auxiliar: En)
3. Operación de vistazo en la estructura de datos Min-Heap:
Para acceder al elemento mínimo (es decir, la raíz del montón), se devuelve el valor del nodo raíz. La complejidad temporal de un vistazo en un montón mínimo es O (1).
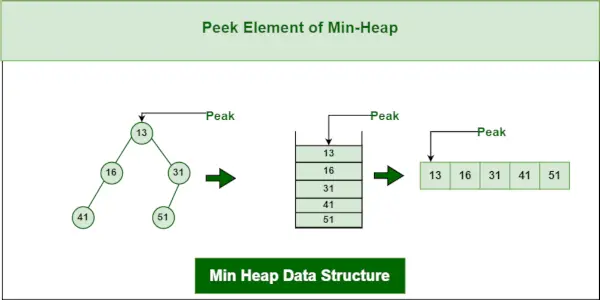
Estructura de datos del montón mínimo
Implementación de la operación Peek en Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , mayor que > minMontón; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Obtener el elemento pico (es decir, el elemento más grande) int peakElement = minHeap.top(); // Imprime el elemento pico cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = nueva PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Obtener el elemento pico (es decir, el elemento más grande) int peakElement = minHeap.peek(); // Imprime el elemento pico System.out.println('Elemento pico: ' + peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Obtener el elemento pico (es decir, el elemento más pequeño) int peakElement = minHeap.Peek(); // Imprime el elemento pico Console.WriteLine('Elemento pico: ' + peakElement); } }> JavaScript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a-b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Obtener el elemento pico (es decir, el elemento más pequeño) const peakElement = minHeap.peek(); // Imprime el elemento pico console.log(`Elemento pico: ${peakElement}`);> Producción
Peak element: 1>
Complejidad del tiempo : En un montón mínimo implementado usando una matriz o una lista, se puede acceder al elemento pico en tiempo constante, O(1), ya que siempre está ubicado en la raíz del montón.
En un montón mínimo implementado mediante un árbol binario, también se puede acceder al elemento pico en tiempo O(1), ya que siempre está ubicado en la raíz del árbol.
novios y dfs
Espacio Auxiliar: En)
4. Operación Heapify en la estructura de datos Min-Heap:
Se puede utilizar una operación heapify para crear un montón mínimo a partir de una matriz sin clasificar. Esto se hace comenzando en el último nodo que no es hoja y realizando repetidamente la operación de burbuja hasta que todos los nodos cumplan con la propiedad del montón.
Operación Heapify en Min Heap
Implementación de la operación Heapify en Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int más pequeño = i; intl = 2*i + 1; intr = 2*i + 2; si (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector salida = {10, 5, 15, 2, 20, 30}; corte<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); corte<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Suponemos que la raíz es el elemento más pequeño inicialmente int más pequeño = i; // Calcula los índices de los hijos izquierdo y derecho del nodo actual int l = 2 * i + 1; int r = 2 * yo + 2; // Compara el hijo izquierdo con el más pequeño actual if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Matriz original: '); // Imprime la matriz original para (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap después de la operación de acumulación: '); // Imprime el montón mínimo después de la operación de apilamiento para (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Pitón def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int más pequeño = i; int izquierda = 2 * i + 1; int derecha = 2 * i + 2; // Compara el hijo izquierdo con el nodo más pequeño actual. si (izquierda< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = nueva lista {10, 5, 15, 2, 20, 30}; Console.Write('Matriz original: '); foreach (int num en arr) Console.Write(num + ' '); // Realizar la operación heapify en el min-heap. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap después de la operación de acumulación: '); foreach (int num en arr) Console.Write(num + ' '); } }> JavaScript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // Imprime el montón mínimo después de la operación de apilamiento console.log('Min-Heap después de la operación de apilamiento: ' + arr.join(' ')); } // Llama a la función principal para iniciar el proceso main();> Producción
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
La complejidad temporal de heapify en un montón mínimo es O (n).
5. Operación de búsqueda en la estructura de datos Min-Heap:
Para buscar un elemento en el montón mínimo, se puede realizar una búsqueda lineal sobre la matriz que representa el montón. Sin embargo, la complejidad temporal de una búsqueda lineal es O(n), lo que no es eficiente. Por lo tanto, la búsqueda no es una operación comúnmente utilizada en un montón mínimo.
Aquí hay un código de ejemplo que muestra cómo buscar un elemento en un montón mínimo usando std::buscar() :
C++ #include using namespace std; int main() { priority_queue , mayor que > min_heap; // ejemplo montón máximo min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); elemento entero = 6; // elemento a buscar bool encontrado = false; // Copia el montón mínimo a una cola temporal y busca // el elemento std::priority_queue , mayor que > temp = min_heap; while (!temp.empty()) { if (temp.top() == elemento) { encontrado = verdadero; romper; } temp.pop(); } si (encontrado) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = nueva PriorityQueue(); min_heap.add(3); // inserta elementos en la cola de prioridad min_heap.offer(1); min_heap.oferta(4); min_heap.oferta(1); min_heap.oferta(6); elemento entero = 6; // elemento a buscar booleano encontrado = false; // Copiar el montón mínimo a una cola temporal y buscar // el elemento PriorityQueue temp = nueva PriorityQueue (min_heap); while (!temp.isEmpty()) { if (temp.poll() == elemento) { encontrado = verdadero; romper; } } if (found) { System.out.println( 'Elemento encontrado en el montón mínimo.'); } else { System.out.println( 'Elemento no encontrado en el montón mínimo.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // ejemplo montón mínimo minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); elemento entero = 6; // elemento a buscar bool encontrado = false; // Copiar el montón mínimo a una cola temporal y buscar // el elemento var temp = new PriorityQueue (minMontón); while (temp.Count> 0) { if (temp.Peek() == elemento) { encontrado = verdadero; romper; } temp.Dequeue(); } if (encontrado) { Console.WriteLine( 'Elemento encontrado en el montón mínimo.'); } else { Console.WriteLine( 'Elemento no encontrado en el montón mínimo.'); } } }> JavaScript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == elemento) { encontrado = verdadero; romper; } temp.dequeue(); } if (found) { console.log('Elemento encontrado en el montón mínimo.'); } else { console.log('Elemento no encontrado en el montón mínimo.'); }> Producción
Element found in the min heap.>
Análisis de complejidad :
El complejidad del tiempo de este programa es O(n iniciar sesión n) , dónde norte es el número de elementos en la cola de prioridad.
La operación de inserción tiene una complejidad temporal de O(log n) en el peor de los casos, porque es necesario mantener la propiedad del montón. La operación de búsqueda implica copiar la cola de prioridad a una cola temporal y luego atravesar la cola temporal, lo que toma O(n iniciar sesión n) tiempo en el peor de los casos porque cada elemento debe copiarse y extraerse de la cola, y la cola de prioridad debe reconstruirse para cada operación.
El complejidad espacial del programa es En) porque almacena norte elementos en la cola de prioridad y crea una cola temporal con norte elementos.
Aplicaciones de la estructura de datos Min-Heap:
- Ordenación del montón: El montón mínimo se utiliza como componente clave en el algoritmo de clasificación del montón, que es un algoritmo de clasificación eficiente con una complejidad temporal de O (nlogn).
- Cola de prioridad: Se puede implementar una cola de prioridad utilizando una estructura de datos de montón mínimo donde el elemento con el valor mínimo siempre está en la raíz.
- Algoritmo de Dijkstra: En el algoritmo de Dijkstra, se utiliza un montón mínimo para almacenar los vértices del gráfico con la distancia mínima desde el vértice inicial. El vértice con la distancia mínima siempre está en la raíz del montón.
- Codificación de Huffman: En la codificación de Huffman, se utiliza un montón mínimo para implementar una cola de prioridad para crear un código de prefijo óptimo para un conjunto determinado de caracteres.
- Fusionar K matrices ordenadas: Dadas K matrices ordenadas, podemos fusionarlas en una única matriz ordenada de manera eficiente utilizando una estructura de datos de montón mínimo.
Ventajas de la estructura de datos Min-heap:
- Inserción y eliminación eficientes : El montón mínimo permite la inserción y eliminación rápida de elementos con una complejidad temporal de O (log n), donde n es el número de elementos en el montón.
- Recuperación eficiente del elemento mínimo: El elemento mínimo en un montón mínimo siempre está en la raíz del montón, que se puede recuperar en tiempo O(1).
- Espacio eficiente: Min heap es una estructura de datos compacta que se puede implementar mediante una matriz o un árbol binario, lo que la hace eficiente en cuanto a espacio.
- Clasificación: El montón mínimo se puede utilizar para implementar un algoritmo de clasificación eficiente, como el tipo de montón con una complejidad temporal de O (n log n).
- Cola de prioridad: El montón mínimo se puede utilizar para implementar una cola de prioridad, donde el elemento con la prioridad mínima se puede recuperar de manera eficiente en tiempo O(1).
- Versatilidad: Min heap tiene varias aplicaciones en informática, incluidos algoritmos gráficos, compresión de datos y sistemas de bases de datos.
En general, min heap es una estructura de datos útil y versátil que ofrece operaciones eficientes, eficiencia de espacio y tiene varias aplicaciones en informática.