A Encimera es un dispositivo que almacena (y a veces muestra) el número de veces que ha ocurrido un evento o proceso en particular, a menudo en relación con una señal de reloj. Los contadores se utilizan en electrónica digital con fines de conteo, pueden contar eventos específicos que ocurren en el circuito. Por ejemplo, en el contador ARRIBA, un contador aumenta la cuenta para cada flanco ascendente del reloj. No solo contando, un contador puede seguir una secuencia determinada según nuestro diseño, como cualquier secuencia aleatoria 0,1,3,2…. También se pueden diseñar con la ayuda de chanclas. Se utilizan como divisores de frecuencia donde se divide la frecuencia de una forma de onda de pulso determinada. Los contadores son circuitos secuenciales que cuentan el número de pulsos y pueden estar en código binario o en formato BCD. Las principales propiedades de un contador son la sincronización, la secuenciación y el conteo. El contador funciona en dos modos.
contador
contador hacia abajo
Clasificación de contador
Los contadores se dividen en términos generales en dos categorías.
- Contador asíncrono
- Contador sincrónico
1. Contador asíncrono
En el contador asíncrono no utilizamos un reloj universal, solo el primer flip-flop es controlado por el reloj principal y la entrada de reloj del resto del siguiente flip-flop es controlada por la salida de los flip-flops anteriores. Podemos entenderlo siguiendo el diagrama.
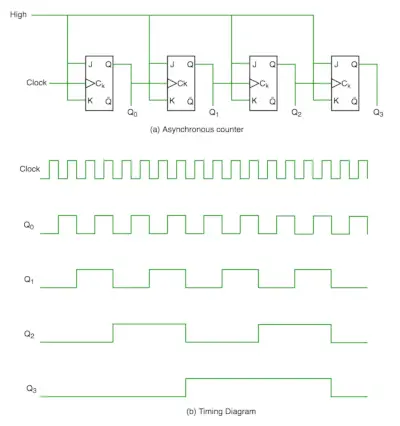
Del diagrama de tiempos se desprende claramente que Q0 cambia tan pronto como se encuentra el flanco ascendente del pulso del reloj, Q1 cambia cuando se encuentra el flanco ascendente de Q0 (porque Q0 es como el pulso de reloj para el segundo flip-flop) y así sucesivamente. De esta manera se generan ondas a través de Q0, Q1, Q2, Q3, por lo que también se le llama Contador RIPPLE y contador en serie. Un contador de ondulación es una disposición en cascada de flip-flops donde la salida de un flip-flop controla la entrada de reloj del siguiente flip-flop.
2. Contador sincrónico
A diferencia del contador asíncrono, el contador síncrono tiene un reloj global que impulsa cada flip-flop para que la salida cambie en paralelo. La única ventaja del contador síncrono sobre el contador asíncrono es que puede funcionar a una frecuencia más alta que el contador asíncrono, ya que no tiene un retraso acumulativo debido a que se le asigna el mismo reloj a cada flip-flop. También se le llama contador paralelo.
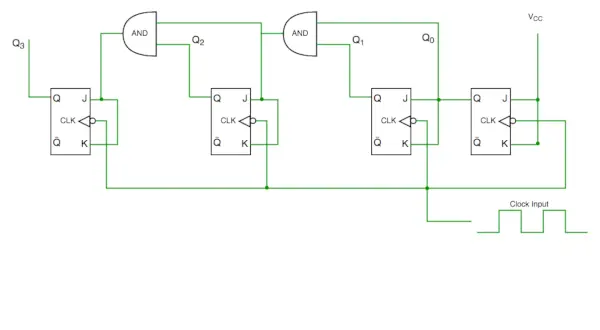
Circuito contador síncrono
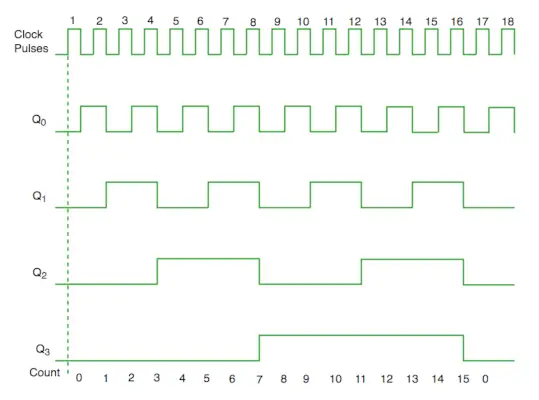
Contador síncrono del diagrama de tiempos
En el diagrama del circuito vemos que el bit Q0 da respuesta a cada flanco descendente del reloj, mientras que Q1 depende de Q0, Q2 depende de Q1 y Q0, Q3 depende de Q2, Q1 y Q0.
Contador de décadas
Un contador de décadas cuenta diez estados diferentes y luego se reinicia a sus estados iniciales. Un contador de décadas simple contará de 0 a 9, pero también podemos crear contadores de décadas que puedan pasar por diez estados cualesquiera entre 0 y 15 (para un contador de 4 bits).
| Pulso del reloj | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Tabla de verdad para contador de décadas simple
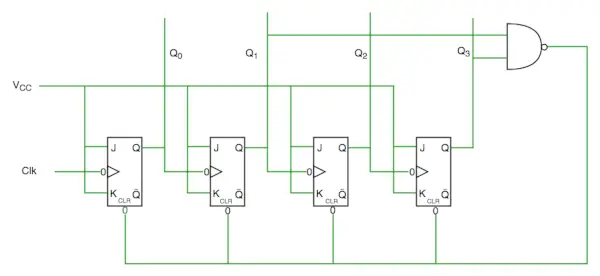
Diagrama del circuito del contador de décadas
Vemos en el diagrama del circuito que hemos usado la puerta nand para Q3 y Q1 y la hemos alimentado para borrar la línea de entrada porque la representación binaria de 10 es:
1010
Y vemos que Q3 y Q1 son 1 aquí, si le damos NAND a estos dos bits para borrar la entrada, entonces el contador se borrará en 10 y nuevamente comenzará desde el principio.
Punto importante : El número de chanclas utilizadas en el contador siempre es mayor que igual a ( registro2norte ) donde n=número de estados en el contador.
Algunas preguntas de puerta de años anteriores sobre contadores
P1. Considere la implementación parcial de un contador de 2 bits utilizando flip-flops T siguiendo la secuencia 0-2-3-1-0, como se muestra a continuación.
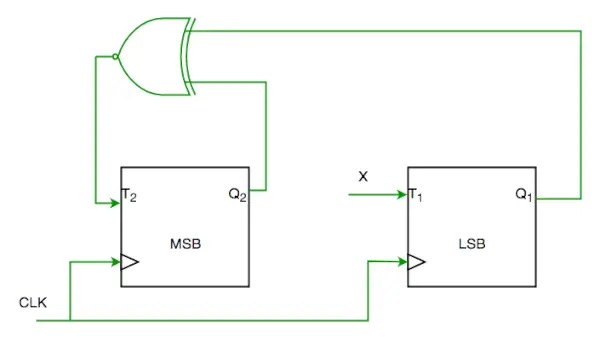
Para completar el circuito, la entrada X debe ser
(A) ¿P2?
(B) Q2 + Q1
(C) (P1 ? P2)’
(D) ¿P1? Q2 (GATE-CS-2004)
Solución:
Del circuito vemos
T1=XQ1’+X’Q1—-(1)
Y
T2=(Q2 ? Q1)’—-(2)
Y LA SALIDA DESEADA ES 00->10->11->01->00
ASI DEBE SER X Q1Q2’+Q1’Q2 SATISFACTORIO 1 Y 2.
ASÍ QUE ANS ES (D) PARTE.
P2. Las funciones de la señal de control de un contador binario de 4 bits se detallan a continuación (donde X no importa)
El contador está conectado de la siguiente manera:
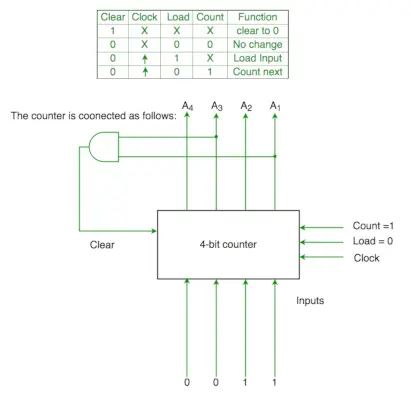
Suponga que los retrasos en el contador y en la puerta son insignificantes. Si el contador comienza en 0, recorre la siguiente secuencia:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
Solución:
Inicialmente A1 A2 A3 A4 =0000
Clr=A1 y A3
Entonces, cuando A1 y A3 son 1, vuelve a ser 0000.
Por lo tanto 0000(init.) -> 0001(A1 y A3=0)->0010 (A1 y A3=0) -> 0011(A1 y A3=0) -> 0100 ( A1 y A3=1 )[condición clara cumplida] ->0000(init.) por lo que pasa por 0->1->2->3->4
La respuesta es la parte (C).
tupla de clasificación de Python
Cuestionario sobre lógica digital
Artículo aportado por Anuj Batham,
