A montón binario es un árbol binario completo que se utiliza para almacenar datos de manera eficiente para obtener el elemento máximo o mínimo según su estructura.
Un montón binario es un montón mínimo o un montón máximo. En un montón binario mínimo, la clave en la raíz debe ser la mínima entre todas las claves presentes en el montón binario. La misma propiedad debe ser verdadera de forma recursiva para todos los nodos del árbol binario. Max Binary Heap es similar a MinHeap.
Ejemplos de montón mínimo:
10 10
/ /
20 100 15 30
/ / /
30 40 50 100 40
¿Cómo se representa el montón binario?
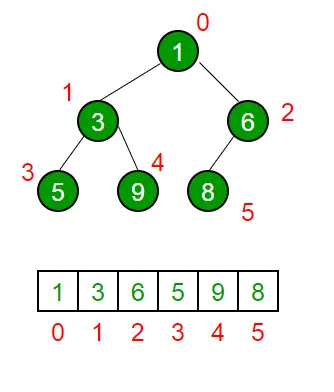
Un montón binario es un Árbol binario completo . Un montón binario normalmente se representa como una matriz.
- El elemento raíz estará en Arr[0].
- La siguiente tabla muestra índices de otros nodos para el ithnodo, es decir, Arr[i]:
| Arr[(i-1)/2] | Devuelve el nodo padre |
| Arr[(2*i)+1] | Devuelve el nodo secundario izquierdo |
| Arr[(2*i)+2] | Devuelve el nodo secundario correcto |
El método transversal utilizado para lograr la representación de matriz es Recorrido de orden de nivel . Por favor refiérase a Representación de matriz del montón binario para detalles.
Operaciones en montón:
A continuación se muestran algunas operaciones estándar en el montón mínimo:
- obtenerMin(): Devuelve el elemento raíz de Min Heap. El tiempo La complejidad de esta operación es O(1) . En el caso de un maxheap sería obtenerMax() .
- extraerMin() : Elimina el elemento mínimo de MinHeap. La Complejidad temporal de esta Operación es O(logN) ya que esta operación necesita mantener la propiedad del montón (llamando amontonar() ) después de quitar la raíz.
- disminuirClave() : Disminuye el valor de la clave. La complejidad temporal de esta operación es O(logN) . Si el valor clave disminuido de un nodo es mayor que el valor principal del nodo, entonces no necesitamos hacer nada. De lo contrario, debemos recorrer hacia arriba para corregir la propiedad del montón violada.
- insertar() : Insertar una nueva clave requiere O(logN) tiempo. Agregamos una nueva clave al final del árbol. Si la nueva clave es mayor que su clave principal, entonces no necesitamos hacer nada. De lo contrario, debemos recorrer hacia arriba para corregir la propiedad del montón violada.
- borrar() : Eliminar una clave también requiere O(logN) tiempo. Reemplazamos la clave a eliminar por la mínima infinita llamando disminuirClave() . Después de disminuirKey(), el valor menos infinito debe llegar a la raíz, por lo que llamamos extraerMin() para quitar la llave.
A continuación se muestra la implementación de operaciones básicas de montón.
C++
// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>'
Overflow: Could not insertKey
'>;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>Harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>Harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest != i) { swap(&harr[i], &harr[smallest]); MinHeapify(smallest); } } // A utility function to swap two elements void swap(int *x, int *y) { int temp = *x; *x = *y; *y = temp; } // Driver program to test above functions int main() { MinHeap h(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); cout << h.extractMin() << ' '; cout << h.getMin() << ' '; h.decreaseKey(2, 1); cout << h.getMin(); return 0; }> |
>
>
actor zeenat aman
Java
// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0> && heapArray[i] swap(heapArray, i, parent(i)); i = parent(i); } return true; } // Decreases value of given key to new_val. // It is assumed that new_val is smaller // than heapArray[key]. public void decreaseKey(int key, int new_val) { heapArray[key] = new_val; while (key != 0 && heapArray[key] swap(heapArray, key, parent(key)); key = parent(key); } } // Returns the minimum key (key at // root) from min heap public int getMin() { return heapArray[0]; } // Method to remove minimum element // (or root) from min heap public int extractMin() { if (current_heap_size <= 0) { return Integer.MAX_VALUE; } if (current_heap_size == 1) { current_heap_size--; return heapArray[0]; } // Store the minimum value, // and remove it from heap int root = heapArray[0]; heapArray[0] = heapArray[current_heap_size - 1]; current_heap_size--; MinHeapify(0); return root; } // This function deletes key at the // given index. It first reduced value // to minus infinite, then calls extractMin() public void deleteKey(int key) { decreaseKey(key, Integer.MIN_VALUE); extractMin(); } // A recursive method to heapify a subtree // with the root at given index // This method assumes that the subtrees // are already heapified private void MinHeapify(int key) { int l = left(key); int r = right(key); int smallest = key; if (l smallest = l; } if (r smallest = r; } if (smallest != key) { swap(heapArray, key, smallest); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } // Driver Code class MinHeapTest { public static void main(String[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); System.out.print(h.extractMin() + ' '); System.out.print(h.getMin() + ' '); h.decreaseKey(2, 1); System.out.print(h.getMin()); } } // This code is contributed by rishabmalhdijo> |
>
>
Pitón
# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>self>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
administrador de tareas para linux
>
C#
// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if> (l heapArray[l] { smallest = l; } if (r heapArray[r] { smallest = r; } if (smallest != key) { Swap(ref heapArray[key], ref heapArray[smallest]); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] { increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } static class MinHeapTest{ // Driver code public static void Main(string[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); Console.Write(h.extractMin() + ' '); Console.Write(h.getMin() + ' '); h.decreaseKey(2, 1); Console.Write(h.getMin()); } } // This code is contributed by // Dinesh Clinton Albert(dineshclinton)> |
>
>
JavaScript
¿Dónde está la configuración del navegador?
// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arreglo[>this>.parent(i)]>arreglo[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arreglo[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]] this.MinHeapify(smallest); } } } let h = new MinHeap(); h.insert(3); h.insert(2); h.deleteKey(1); h.insert(15); h.insert(5); h.insert(4); h.insert(45); console.log(h.extractMin() + ' '); console.log(h.getMin() + ' '); h.decreaseKey(2, 1); console.log(h.extractMin());> |
>
>Producción
2 4 1>
Aplicaciones de montones:
- Ordenar montón : Heap Sort utiliza Binary Heap para ordenar una matriz en tiempo O (nLogn).
- Cola de prioridad: Las colas de prioridad se pueden implementar de manera eficiente utilizando Binary Heap porque admite operaciones insert(), delete() y extractmax(), disminuyKey() en tiempo O(log N). Binomial Heap y Fibonacci Heap son variaciones de Binary Heap. Estas variaciones realizan la unión también de manera eficiente.
- Algoritmos de gráficos: las colas de prioridad se utilizan especialmente en algoritmos de gráficos como El camino más corto de Dijkstra y Árbol de expansión mínima de Prim .
- Muchos problemas se pueden resolver de manera eficiente utilizando Heaps. Consulte lo siguiente, por ejemplo. a) K'th elemento más grande en una matriz . b) Ordenar una matriz casi ordenada/ C) Fusionar K matrices ordenadas .
Enlaces relacionados:
- Práctica de codificación en montón
- Todos los artículos sobre el montón
- PriorityQueue: Implementación del montón binario en la biblioteca Java
