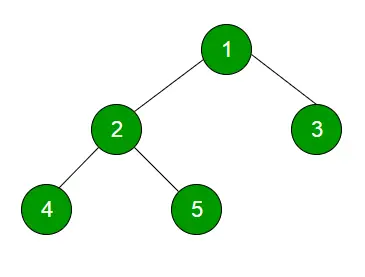
Recorrido de orden de nivel La técnica se define como un método para atravesar un árbol de modo que todos los nodos presentes en el mismo nivel se atraviesen por completo antes de atravesar el siguiente nivel.

Ejemplo:
Práctica recomendada Recorrido de orden de nivel ¡Pruébelo!Aporte:
Producción:
1
2 3
4 5
¿Cómo funciona el recorrido de orden de nivel?
La idea principal del recorrido del orden de niveles es atravesar todos los nodos de un nivel inferior antes de pasar a cualquiera de los nodos de un nivel superior. Esto se puede hacer de cualquiera de las siguientes maneras:
- el ingenuo (encontrar la altura del árbol y atravesar cada nivel e imprimir los nodos de ese nivel)
- utilizando eficientemente una cola.
Recorrido de orden de nivel (enfoque ingenuo):
Encontrar altura de árbol. Luego, para cada nivel, ejecute una función recursiva manteniendo la altura actual. Siempre que el nivel de un nodo coincida, imprima ese nodo.
A continuación se muestra la implementación del enfoque anterior:
C++ // Recursive CPP program for level // order traversal of Binary Tree #include using namespace std; // A binary tree node has data, // pointer to left child // and a pointer to right child class node { public: int data; node *left, *right; }; // Function prototypes void printCurrentLevel(node* root, int level); int height(node* node); node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(node* root, int level) { if (root == NULL) return; if (level == 1) cout << root->datos<< ' '; else if (level>1) { printCurrentLevel(raíz->izquierda, nivel - 1); printCurrentLevel(raíz->derecha, nivel - 1); } } // Calcula la 'altura' de un árbol: el número de // nodos a lo largo del camino más largo desde el nodo raíz // hasta el nodo hoja más lejano. int altura(nodo* nodo) { if (nodo == NULL) devuelve 0; else { // Calcula la altura de cada subárbol int lheight = height(node->left); int rheight = altura(nodo->derecha); // Usa el más grande if (altura> altura) { return (altura + 1); } else { retorno (altura + 1); } } } // Función auxiliar que asigna // un nuevo nodo con los datos dados y // punteros NULL izquierdo y derecho. nodo* nuevoNodo(int datos) { nodo* Nodo = nuevo nodo(); Nodo->datos = datos; Nodo->izquierda = NULL; Nodo->derecha = NULL; retorno (nodo); } // Código del controlador int main() { nodo* raíz = nuevoNodo(1); raíz->izquierda = nuevoNodo(2); raíz->derecha = nuevoNodo(3); raíz->izquierda->izquierda = nuevoNodo(4); raíz->izquierda->derecha = nuevoNodo(5); corte<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; } // This code is contributed by rathbhupendra> C // Recursive C program for level // order traversal of Binary Tree #include #include // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node *left, *right; }; // Function prototypes void printCurrentLevel(struct node* root, int level); int height(struct node* node); struct node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(struct node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(struct node* root, int level) { if (root == NULL) return; if (level == 1) printf('%d ', root->datos); else if (nivel> 1) { printCurrentLevel(raíz->izquierda, nivel - 1); printCurrentLevel(raíz->derecha, nivel - 1); } } // Calcula la 'altura' de un árbol - el número de // nodos a lo largo del camino más largo desde el nodo raíz // hasta el nodo hoja más lejano int height(struct node* node) { if (node == NULL) devuelve 0; else { // Calcula la altura de cada subárbol int lheight = height(node->left); int rheight = altura(nodo->derecha); // Usa el más grande if (altura> altura) return (altura + 1); de lo contrario regresa (altura + 1); } } // Función auxiliar que asigna un nuevo nodo con los // datos dados y los punteros NULL izquierdo y derecho. nodo de estructura* nuevoNodo(int datos) { nodo de estructura* nodo = (nodo de estructura*)malloc(tamañode(nodo de estructura)); nodo->datos = datos; nodo->izquierda = NULL; nodo->derecha = NULL; retorno (nodo); } // Programa controlador para probar las funciones anteriores int main() { struct node* root = newNode(1); raíz->izquierda = nuevoNodo(2); raíz->derecha = nuevoNodo(3); raíz->izquierda->izquierda = nuevoNodo(4); raíz->izquierda->derecha = nuevoNodo(5); printf('El recorrido del orden de nivel del árbol binario es
'); printLevelOrder(raíz); devolver 0; }> Java // Recursive Java program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class BinaryTree { // Root of the Binary Tree Node root; public BinaryTree() { root = null; } // Function to print level order traversal of tree void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number of // nodes along the longest path from the root node // down to the farthest leaf node. int height(Node root) { if (root == null) return 0; else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>altura) retorno (altura + 1); de lo contrario regresa (altura + 1); } } // Imprime nodos en el nivel actual void printCurrentLevel(Raíz del nodo, nivel int) { if (root == null) return; if (nivel == 1) System.out.print(root.data + ' '); else if (nivel> 1) { printCurrentLevel(root.left, nivel - 1); printCurrentLevel(raíz.derecha, nivel - 1); } } // Programa controlador para probar las funciones anteriores public static void main(String args[]) { BinaryTree tree = new BinaryTree(); árbol.root = nuevo Nodo(1); tree.root.left = nuevo Nodo(2); tree.root.right = nuevo Nodo(3); tree.root.left.left = nuevo Nodo(4); tree.root.left.right = nuevo Nodo(5); System.out.println('El recorrido del orden de nivel de' + 'árbol binario es '); árbol.printLevelOrder(); } }> Pitón # Recursive Python program for level # order traversal of Binary Tree # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Function to print level order traversal of tree def printLevelOrder(root): h = height(root) for i in range(1, h+1): printCurrentLevel(root, i) # Print nodes at a current level def printCurrentLevel(root, level): if root is None: return if level == 1: print(root.data, end=' ') elif level>1: printCurrentLevel(root.left, nivel-1) printCurrentLevel(root.right, nivel-1) # Calcula la altura de un árbol: el número de nodos # a lo largo del camino más largo desde el nodo raíz hasta # la hoja más alejada node def altura(nodo): si el nodo es Ninguno: devuelve 0; de lo contrario: # Calcula la altura de cada subárbol altura = altura(nodo.izquierda) altura = altura(nodo.derecha) # Usa el más grande si altura> altura: retorno altura+1 más: devuelve altura+1 # Programa controlador para probar la función anterior si __nombre__ == '__main__': raíz = Nodo(1) raíz.izquierda = Nodo(2) raíz.derecha = Nodo(3) raíz. left.left = Node(4) root.left.right = Node(5) print('El recorrido del orden de nivel del árbol binario es -') printLevelOrder(root) # Este código es una contribución de Nikhil Kumar Singh(nickzuck_007)> C# // Recursive c# program for level // order traversal of Binary Tree using System; // Class containing left and right // child of current node and key value public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { // Root of the Binary Tree public Node root; public void BinaryTree() { root = null; } // Function to print level order // traversal of tree public virtual void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) { printCurrentLevel(root, i); } } // Compute the 'height' of a tree -- // the number of nodes along the longest // path from the root node down to the // farthest leaf node. public virtual int height(Node root) { if (root == null) { return 0; } else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>altura) { return (altura + 1); } else { retorno (altura + 1); } } } // Imprime nodos en el nivel actual public virtual void printCurrentLevel(Raíz del nodo, nivel int) { if (root == null) { return; } if (nivel == 1) { Console.Write(root.data + ' '); } else if (nivel> 1) { printCurrentLevel(root.left, nivel - 1); printCurrentLevel(raíz.derecha, nivel - 1); } } // Código del controlador public static void Main(string[] args) { GFG tree = new GFG(); árbol.root = nuevo Nodo(1); tree.root.left = nuevo Nodo(2); tree.root.right = nuevo Nodo(3); tree.root.left.left = nuevo Nodo(4); tree.root.left.right = nuevo Nodo(5); Console.WriteLine('El recorrido del orden de niveles ' + 'del árbol binario es '); árbol.printLevelOrder(); } } // Este código es aportado por Shrikant13> JavaScript // Recursive javascript program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Root of the Binary Tree var root= null; // Function to print level order traversal of tree function printLevelOrder() { var h = height(root); var i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number // of nodes along the longest path // from the root node down to the farthest leaf node. function height(root) { if (root == null) return 0; else { // Compute height of each subtree var lheight = height(root.left); var rheight = height(root.right); // Use the larger one if (lheight>altura) retorno (altura + 1); de lo contrario regresa (altura + 1); } } // Imprimir nodos en el nivel actual function printCurrentLevel(root, nivel) { if (root == null) return; if (nivel == 1) console.log(root.data + ' '); else if (nivel> 1) { printCurrentLevel(root.left, nivel - 1); printCurrentLevel(raíz.derecha, nivel - 1); } } // Programa controlador para probar las funciones anteriores root = new Node(1); root.left = nuevo Nodo(2); root.right = nuevo Nodo(3); root.left.left = nuevo Nodo(4); root.left.right = nuevo Nodo(5); console.log('El recorrido del orden de niveles del árbol binario es '); imprimirOrdenNivel(); // Este código es aportado por umadevi9616> Producción
Level Order traversal of binary tree is 1 2 3 4 5>
Complejidad del tiempo: O(N), donde N es el número de nodos en el árbol sesgado.
Espacio Auxiliar: O(1) Si se considera la pila de recursividad, el espacio utilizado es O(N).
parámetro en el script de shell
Recorrido de orden de nivel usando Cola
Necesitamos visitar los nodos de un nivel inferior antes que cualquier nodo de un nivel superior, esta idea es bastante similar a la de una cola. Empuje los nodos de un nivel inferior en la cola. Cuando se visita cualquier nodo, saque ese nodo de la cola e inserte al hijo de ese nodo en la cola.
Esto garantiza que el nodo de un nivel inferior sea visitado antes que cualquier nodo de un nivel superior.
A continuación se muestra la implementación del enfoque anterior:
C++ // C++ program to print level order traversal #include using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // Iterative method to find height of Binary Tree void printLevelOrder(Node* root) { // Base Case if (root == NULL) return; // Create an empty queue for level order traversal queueq; // Poner en cola Root e inicializar altura q.push(root); while (q.empty() == false) { // Imprime el frente de la cola y elimínalo de la cola Nodo* nodo = q.front(); corte<< node->datos<< ' '; q.pop(); // Enqueue left child if (node->izquierda != NULL) q.push(nodo->izquierda); // Poner en cola al hijo derecho if (nodo->derecho! = NULL) q.push(nodo->derecho); } } // Función de utilidad para crear un nuevo nodo de árbol Nodo* nuevoNodo(int data) { Nodo* temp = nuevo Nodo; temperatura->datos = datos; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Programa controlador para probar las funciones anteriores int main() { // Creemos el árbol binario que se muestra en el diagrama anterior Nodo* root = newNode(1); raíz->izquierda = nuevoNodo(2); raíz->derecha = nuevoNodo(3); raíz->izquierda->izquierda = nuevoNodo(4); raíz->izquierda->derecha = nuevoNodo(5); corte<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; }> C // Iterative Queue based C program // to do level order traversal // of Binary Tree #include #include #define MAX_Q_SIZE 500 // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node* left; struct node* right; }; // Function prototypes struct node** createQueue(int*, int*); void enQueue(struct node**, int*, struct node*); struct node* deQueue(struct node**, int*); // Given a binary tree, print its nodes in level order // using array for implementing queue void printLevelOrder(struct node* root) { int rear, front; struct node** queue = createQueue(&front, &rear); struct node* temp_node = root; while (temp_node) { printf('%d ', temp_node->datos); // Poner en cola al hijo izquierdo if (temp_node->left) enQueue(queue, &rear, temp_node->left); // Poner en cola al hijo derecho if (temp_node->right) enQueue(queue, &rear, temp_node->right); // Quitar el nodo de la cola y convertirlo en temp_node temp_node = deQueue(queue, &front); } } // Funciones de utilidad struct node** createQueue(int* front, int* rear) { struct node** queue = (struct node**)malloc( sizeof(struct node*) * MAX_Q_SIZE); *delantero = *trasero = 0; cola de retorno; } void enQueue(estructura nodo** cola, int* trasero, estructura nodo* nuevo_nodo) { cola[*trasero] = nuevo_nodo; (*trasero)++; } struct node* deQueue(struct node** cola, int* front) { (*front)++; cola de retorno [* frente - 1]; } // Función auxiliar que asigna un nuevo nodo con los // datos dados y los punteros NULL izquierdo y derecho. nodo de estructura* nuevoNodo(int datos) { nodo de estructura* nodo = (nodo de estructura*)malloc(tamañode(nodo de estructura)); nodo->datos = datos; nodo->izquierda = NULL; nodo->derecha = NULL; retorno (nodo); } // Programa controlador para probar las funciones anteriores int main() { struct node* root = newNode(1); raíz->izquierda = nuevoNodo(2); raíz->derecha = nuevoNodo(3); raíz->izquierda->izquierda = nuevoNodo(4); raíz->izquierda->derecha = nuevoNodo(5); printf('El recorrido del orden de nivel del árbol binario es
'); printLevelOrder(raíz); devolver 0; }> Java // Iterative Queue based Java program // to do level order traversal // of Binary Tree import java.util.LinkedList; import java.util.Queue; // Class to represent Tree node class Node { int data; Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order // using array for implementing queue void printLevelOrder() { Queuecola = nueva lista enlazada(); cola.add(raíz); while (!queue.isEmpty()) { // poll() elimina el encabezado actual. Nodo tempNode = cola.poll(); System.out.print(tempNode.data + ' '); // Poner en cola al hijo izquierdo if (tempNode.left! = null) { queue.add(tempNode.left); } // Poner en cola el hijo derecho if (tempNode.right! = null) { queue.add(tempNode.right); } } } public static void main(String args[]) { // Creando un árbol binario e ingresando // los nodos BinaryTree tree_level = new BinaryTree(); tree_level.root = nuevo Nodo(1); tree_level.root.left = nuevo Nodo(2); tree_level.root.right = nuevo Nodo(3); tree_level.root.left.left = nuevo Nodo(4); tree_level.root.left.right = nuevo Nodo(5); System.out.println('El recorrido del orden de nivel del árbol binario es - '); tree_level.printLevelOrder(); } }> Pitón # Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Imprimir el frente de la cola y # eliminarlo de la cola print(queue[0].data, end=' ') node = queue.pop(0) # Poner en cola el hijo izquierdo si node.left no es Ninguno: queue.append(node.left) # Poner en cola el hijo derecho si node.right no es Ninguno: queue.append(node.right) # Programa controlador para probar la función anterior si __name__ == '__main__': root = Node(1 ) root.left = Nodo(2) root.right = Nodo(3) root.left.left = Nodo(4) root.left.right = Nodo(5) print('Orden de nivel El recorrido del árbol binario es - ') printLevelOrder(root) # Este código es una contribución de Nikhil Kumar Singh(nickzuck_007)> C# // Iterative Queue based C# program // to do level order traversal // of Binary Tree using System; using System.Collections.Generic; // Class to represent Tree node public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal public class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order using // array for implementing queue void printLevelOrder() { Queuecola = nueva cola(); cola.En cola (raíz); while (queue.Count != 0) { Nodo tempNode = cola.Dequeue(); Console.Write(tempNode.data + ' '); // Poner en cola al hijo izquierdo if (tempNode.left! = null) { queue.Enqueue(tempNode.left); } // Poner en cola el hijo derecho if (tempNode.right! = null) { queue.Enqueue(tempNode.right); } } } // Código del controlador public static void Main() { // Creando un árbol binario e ingresando // los nodos BinaryTree tree_level = new BinaryTree(); tree_level.root = nuevo Nodo(1); tree_level.root.left = nuevo Nodo(2); tree_level.root.right = nuevo Nodo(3); tree_level.root.left.left = nuevo Nodo(4); tree_level.root.left.right = nuevo Nodo(5); Console.WriteLine('El recorrido del orden de niveles ' + 'del árbol binario es - '); tree_level.printLevelOrder(); } } // Este código fue aportado por PrinciRaj1992> JavaScript class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Class to represent a deque (double-ended queue) class Deque { constructor() { this.queue = []; } // Method to add an element to the end of the queue enqueue(item) { this.queue.push(item); } // Method to remove and return the first element of the queue dequeue() { return this.queue.shift(); } // Method to check if the queue is empty isEmpty() { return this.queue.length === 0; } } // Function to perform level order traversal of a binary tree function printLevelOrder(root) { // Create a deque to store nodes for traversal const queue = new Deque(); // Add the root node to the queue queue.enqueue(root); // Continue traversal until the queue is empty while (!queue.isEmpty()) { // Remove and get the first node from the queue const tempNode = queue.dequeue(); // Print the data of the current node console.log(tempNode.data + ' '); // Enqueue the left child if it exists if (tempNode.left !== null) { queue.enqueue(tempNode.left); } // Enqueue the right child if it exists if (tempNode.right !== null) { queue.enqueue(tempNode.right); } } } // Create a binary tree and enter the nodes const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); // Print the level order traversal of the binary tree console.log('Level order traversal of binary tree is - '); printLevelOrder(root);> Producción
Level Order traversal of binary tree is 1 2 3 4 5>
Complejidad del tiempo: O(N) donde N es el número de nodos en el árbol binario.
Espacio Auxiliar: O(N) donde N es el número de nodos en el árbol binario.