conocemos un árbol es una estructura de datos no lineal. No tiene limitación en el número de hijos. A¿Qué es un árbol binario completo?

Un árbol binario completo es un tipo especial de árbol binario en el que todos los niveles del árbol se llenan por completo, excepto los nodos del nivel más bajo, que se llenan lo más hacia la izquierda posible.

Árbol binario completo

Alguna terminología del árbol binario completo:

• Raíz – Nodo en el que no proviene ningún borde del padre. Ejemplo: nodo A
• Niño – El nodo que tiene alguna ventaja entrante se llama hijo. Ejemplo: los nodos B, F son hijos de A y C respectivamente.
• Hermano – Los nodos que tienen el mismo padre son hermanos. Ejemplo: D, E son hermanos porque tienen el mismo padre B.
• Grado de un nodo – Número de hijos de un padre en particular. Ejemplo: el grado de A es 2 y el grado de C es 1. El grado de D es 0.
• Nodos internos/externos – Los nodos hoja son nodos externos y los nodos no hoja son nodos internos.
• Nivel – Cuente los nodos en una ruta para llegar a un nodo de destino. Ejemplo: el nivel del nodo D es 2 ya que los nodos A y B forman la ruta.
• Altura – Número de aristas para llegar al nodo de destino, la raíz está en la altura 0. Ejemplo – La altura del nodo E es 2 ya que tiene dos aristas desde la raíz.

Propiedades del árbol binario completo:

• Se dice que un árbol binario completo es un árbol binario adecuado donde todas las hojas tienen la misma profundidad.
• En un árbol binario completo, número de nodos en profundidad. d es 2 ^d .
• En un árbol binario completo con norte La altura de los nodos del árbol es. iniciar sesión(n+1) .
• todos los niveles excepto el último nivel están completamente llenos.

Árbol binario perfecto vs árbol binario completo:

Un árbol binario de altura 'h' que tiene el número máximo de nodos es un perfecto árbol binario.
Para una altura determinada h , el número máximo de nodos es 2 ^h+1 -1 .

A completo El árbol binario de altura h es un árbol binario perfecto hasta la altura. h-1 , y en el último nivel los elementos se almacenan en orden de izquierda a derecha.

Ejemplo 1:

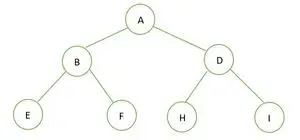
Un árbol binario

La altura del árbol binario dado es 2 y el número máximo de nodos en ese árbol es n= 2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Por lo tanto podemos concluir que es un árbol binario perfecto .
Ahora, para un árbol binario completo, está lleno hasta la altura. h-1 es decir.; 1, y los elementos del último nivel se almacenan en orden de izquierda a derecha. Por tanto, también es un árbol binario completo. Aquí está la representación de los elementos cuando se almacenan en una matriz.

Elemento almacenado en una matriz nivel por nivel

En la matriz, todos los elementos se almacenan continuamente.

Ejemplo 2:

año mes

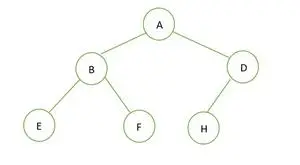
Un árbol binario

La altura del árbol binario dado es 2 y el número máximo de nodos que debería haber allí es 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Pero el número de nodos en el árbol es 6 . Por lo tanto es no es un árbol binario perfecto .
Ahora, para un árbol binario completo, está lleno hasta la altura. h-1 es decir.; 1 y el elemento del último nivel se almacenan en orden de izquierda a derecha. Por lo tanto este es un árbol binario completo . Almacene el elemento en una matriz y será como;

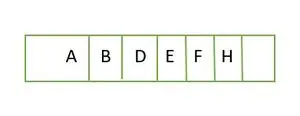
Elemento almacenado en una matriz nivel por nivel

Ejemplo 3:

longitud de la cadena java

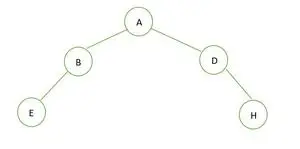
Un árbol binario

La altura del árbol binario es 2 y el número máximo de nodos que puede haber allí es 7, pero solo hay 5 nodos, por lo tanto es no es un árbol binario perfecto .
En el caso de un árbol binario completo, vemos que en el último nivel los elementos no se llenan de izquierda a derecha. Así es no es un árbol binario completo .

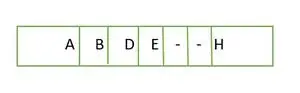
Elemento almacenado en una matriz nivel por nivel

Los elementos de la matriz no son continuos.

Árbol binario completo versus árbol binario completo:

Para un árbol binario completo, cada nodo tiene 2 hijos o 0 hijos.

Ejemplo 1:

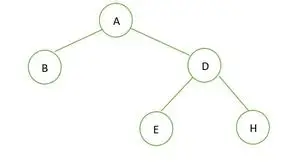
Un árbol binario

En el árbol binario dado no hay ningún nodo que tenga grado 1, ya sea 2 o 0 hijos para cada nodo, por lo tanto, es un árbol binario completo .

Para un árbol binario completo, los elementos se almacenan nivel por nivel y no desde el lado izquierdo en el último nivel. Por lo tanto esto es no es un árbol binario completo . La representación de la matriz es:

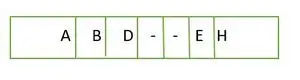
Elemento almacenado en una matriz nivel por nivel

Ejemplo 2:

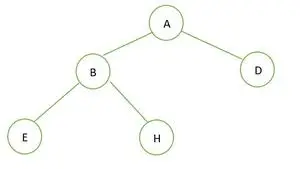
Un árbol binario

En el árbol binario dado no hay ningún nodo que tenga grado 1. Cada nodo tiene un grado de 2 o 0. Por lo tanto, es un árbol binario completo .

Para un árbol binario completo, los elementos se almacenan nivel por nivel y se llenan desde el lado izquierdo del último nivel. De ahí que este sea un árbol binario completo . A continuación se muestra la representación de matriz del árbol:

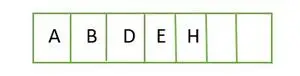
Elemento almacenado en una matriz nivel por nivel

Ejemplo 3:

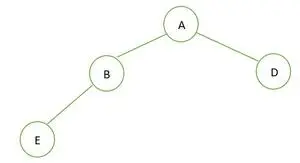
Un árbol binario

En el árbol binario dado, el nodo B tiene grado 1, lo que viola la propiedad del árbol binario completo, por lo que es no es un árbol binario completo

mecanografiado para cada uno

Para un árbol binario completo, los elementos se almacenan nivel por nivel y se llenan desde el lado izquierdo del último nivel. Por lo tanto este es un árbol binario completo . La representación de matriz del árbol binario es:

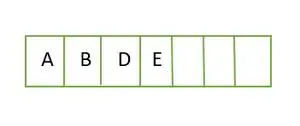
Elemento almacenado en una matriz nivel por nivel

Ejemplo 4:

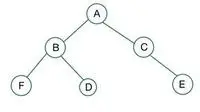
un árbol binario

En el árbol binario dado, el nodo C tiene grado 1, lo que viola la propiedad de un árbol binario completo, por lo que es no es un árbol binario completo

Para un árbol binario completo, los elementos se almacenan nivel por nivel y se llenan desde el lado izquierdo del último nivel. Aquí el nodo E viola la condición. Por lo tanto esto es no es un árbol binario completo .

Creación de árbol binario completo:

conocemos un árbol binario completo es un árbol en el que, excepto el último nivel (digamos yo )todo el otro nivel tiene ( 2 litros ) nodos y los nodos están alineados de izquierda a derecha.
Se puede representar mediante una matriz. Si el padre es el índice i entonces el niño izquierdo está en 2i+1 y el niño correcto está en 2i+2 .

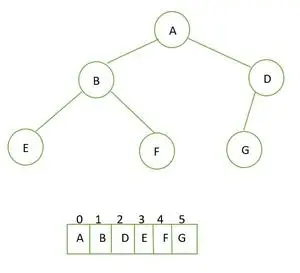
Árbol binario completo y su representación en matriz.

Algoritmo:

Para la creación de un Árbol binario completo , requerimos un Paso 1: Inicialice la raíz con un nuevo nodo cuando el árbol esté vacío.

Paso 2: Si el árbol no está vacío, obtenga el elemento frontal.

jsp

• Si el elemento frontal no tiene un hijo izquierdo, establezca el hijo izquierdo en un nuevo nodo
• Si el hijo correcto no está presente, establezca el hijo correcto como un nuevo nodo

Paso 3: Si el nodo tiene ambos hijos, entonces estallido sacarlo de la cola.

Etapa 4: Ponga en cola los nuevos datos.

Ilustración:

Considere la siguiente matriz:

1. El primer elemento será la raíz (valor en el índice = 0 )

A se toma como raíz

2. El siguiente elemento (en el índice = 1 ) quedará a la izquierda y el tercer elemento (índice = 2 ) será el hijo derecho de la raíz

B como hijo izquierdo y D como hijo derecho

3. cuarto (índice = 3 ) y quinto elemento (índice = 4 ) será el hijo izquierdo y derecho del nodo B

E y F son hijos izquierdo y derecho de B

4. Siguiente elemento (índice = 5 ) quedará como hijo del nodo D

protocolos de capa de enlace de datos

G se convierte en hijo izquierdo del nodo D

Así se crea el árbol binario completo.

Implementación: Para la implementación de la construcción de un árbol binario completo a partir del recorrido del orden de niveles se proporciona en esta publicación .

Aplicación del árbol binario completo:

• Ordenar montón
• Estructura de datos basada en clasificación de montón

Compruebe si un árbol binario determinado está completo o no: Seguir esta publicación para comprobar si el árbol binario dado está completo o no.