Ceros de un polinomio son esos valores reales, imaginarios o complejos que cuando se colocan en el polinomio en lugar de una variable, el resultado se vuelve cero (como su nombre indica, cero también). Los polinomios se utilizan para modelar algunos fenómenos físicos que ocurren en la vida real y son muy útiles para describir situaciones matemáticamente.

Los ceros de un polinomio son todos los valores de x que hacen que el polinomio sea igual a cero. Los ceros de un polinomio nos informan sobre las intersecciones con el eje x de la gráfica del polinomio. En este artículo, discutiremos sobre el ceros de un polinomio, cómo encontrarlos, teorema del factor, etc.

Tabla de contenidos

• ¿Qué son los ceros de los polinomios?
• Ceros de fórmula polinomial
• ¿Cómo encontrar el cero de un polinomio?
• Para polinomio lineal
• Para polinomio cuadrático
• Para polinomio cúbico
• Teorema de los factores
• Relación entre Ceros y Coeficiente
• Relación entre ceros y coeficiente para ecuación cuadrática
• Relación entre ceros y coeficiente para ecuación cúbica
• Formar ecuaciones con ceros de polinomio
• Ceros en gráfica de polinomios
• Teorema fundamental del álgebra lineal
• Multiplicidad de una raíz
• Artículos relacionados con Ceros de Polinomio
• Problemas de muestra sobre ceros de polinomio
• Problemas de práctica sobre ceros de polinomio

¿Qué son los ceros de los polinomios?

Para un polinomio P(x), decimos que x = a es el cero del polinomio si P(a) = 0, y todos esos ceros de un polinomio se denominan comúnmente ceros de un polinomio. Por ejemplo, considere f(x) = 3x – 12. Ahora, ponga x = 4 en el polinomio, es decir, f(4) = 3×4 – 12 = 0. Por lo tanto, x = 4 es un cero del polinomio f( x) = 3x – 12.

Ejemplo: Para f(x) = x ³ – 6x ² + 11x – 6, ¿es x = 1 cero?

Solución:

Para comprobar si si x = 1 es cero de f(x) = x³– 6x²+ 11x – 6 o no, pon x = 1 en (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Por tanto, x = 1 es un cero de f(x).

Ceros de fórmula polinomial

Para un polinomio lineal de forma ax + b, su cero viene dado por x = -b/a.

Para un polinomio cuadrático de forma ax²+ bx + c, su cero está dado por x = {- b ± √D}/2a donde D es Discriminante dado por b²– 4ac.

¿Cómo encontrar el cero de un polinomio?

Podemos encontrar los ceros del polinomio para varios tipos de polinomios utilizando varios métodos que se analizan a continuación.

• Para polinomio lineal
• Para polinomio cuadrático
• Para polinomio cúbico

Para polinomio lineal

Para los polinomios lineales, encontrar el cero es el más fácil de todos. ya que solo hay un cero y eso también se puede calcular mediante una simple reordenación del polinomio después del polinomio igualador a 0.

Por ejemplo, encuentre cero para el polinomio lineal f(x) = 2x – 7.

Solución:

Para encontrar el cero de f(x), iguale f(x) a 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Para polinomio cuadrático

Existen varios métodos para encontrar raíces o ceros de un polinomio cuadrático, como dividir el término medio, una fórmula cuadrática que también se conoce como fórmula de Shree Dharacharya y completar el cuadrado, que es algo similar a la fórmula cuadrática, como viene la fórmula cuadrática. de completar el cuadrado de la ecuación cuadrática general.

Aprender más acerca de resolver ecuaciones cuadráticas o polinomios y cómo resolverlos. Los siguientes ejemplos muestran en detalle el método para encontrar ceros de polinomios cuadráticos.

Ejemplo 1: Descubra los ceros para P(x) = x ² + 2x – 15.

Respuesta:

X²+ 2x – 15 = 0

⇒x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Ejemplo 2: Encuentre los ceros para P(x) = x ² – 16x+64.

Respuesta:

X²– 16x + 64 = 0

Comparando con el hacha²+ bx + c = 0,

obtenemos, a = 1, b = -16 y c = 64.

De este modo,

⇒ x = 8, 8

Para polinomio cúbico

Para encontrar ceros cúbicos hay muchas formas, como el teorema de la raíz racional y la división larga. Un método para encontrar raíces de polinomio cúbico o de cualquier grado superior es el siguiente:

Paso 1: Utilice el teorema de la raíz racional para encontrar las raíces posibles. es decir, si un polinomio tiene una raíz racional, debe ser la división de p/q, donde p es la constante entera y q es el coeficiente principal.

Paso 2: Después de encontrar una raíz, divide el polinomio con el factor formado por esa raíz usando una división larga y escribe el polinomio como producto de cociente y dividendo.

Paso 3: Si el cociente es una expresión cuadrática, resuélvelo mediante los métodos mencionados anteriormente para polinomios cuadráticos. Si no es un polinomio de grado 2, repita los pasos 1 y 2 hasta que el cociente se convierta en un polinomio de grado 2.

Etapa 4: El resultado del paso 3 son los factores requeridos y, al igualar el factor a 0, podemos encontrar los ceros del polinomio.

Ejemplo: encontrar los ceros del polinomio cúbico p(x) = x ³ + 2x ² – 5x – 6.

Solución:

p(x) = x³+ 2x²– 5x – 6

Como p/q = -6

Según el teorema de la raíz racional, todas las raíces racionales posibles del polunomio son divisores de p/q.

Por tanto, divisores = ±1, ±2, ±3, ±6

x = -1, en p(x), obtenemos

pag(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Por tanto, según el teorema del factor, x + 1 es el factor de p(x).

Así, x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Para ceros, p(x) = 0,

Los ceros de p(x) son x = -1, x = 2 y x = -3.

Teorema de los factores

Para el polinomio P(x), el teorema del factor establece que si x =a es cero de P(X) y si x – a es un factor de P(x). es decir, las dos condiciones siguientes deberían ser ciertas.

• Si a es un cero de P(x) entonces x−a será un factor de P(x)
• Si x−a es un factor de P(x) entonces a será un cero de P(x)

Esto se puede verificar mirando ejemplos anteriores. El teorema del factor puede conducir a algunos resultados interesantes, que son los siguientes:

Resultado 1: Si P(x) es un polinomio de grado n y r es un cero de P(x), entonces P(x) se puede escribir de la siguiente forma,

P(x) = (x – r) Q(x)

Donde Q(x) es un polinomio de grado n-1 y se puede encontrar dividiendo P(x) entre (x – r).

Resultado 2: Si P(x) = (x-r)Q(x) y x = t es un cero de Q(x), entonces x = t también será un cero de P(x).

Para verificar el hecho anterior,

Digamos que t es cero Q(x), lo que significa Q(t) = 0.

Sabemos que r es un cero del polinomio P(x), donde P(x) = (x – r) Q(x),

Entonces necesitamos verificar si x = t también es un cero de P(x), pongamos x = t en P(x)

⇒ P(t) = (t – r) Q(t) = 0

Entonces, x = t también es un cero P(x).

Por lo tanto, probado.

Relación entre Ceros y Coeficiente

La relación entre los ceros y el coeficiente de la ecuación cuadrática y cúbica se analiza a continuación.

Relación entre ceros y coeficiente para ecuación cuadrática

Para una ecuación cuadrática de la forma ax²+ bx + c = 0, si los dos ceros de la ecuación cuadrática son α y β, entonces

• Suma de raíz = α + β = -b/a
• Producto de raíces = α × β = c/a

Relación entre ceros y coeficiente para ecuación cúbica

Si α, β y γ son la raíz del polinomio cúbico ax³+ bx²+ cx + d = 0, entonces la relación entre sus ceros y coeficientes viene dada de la siguiente manera:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Formar ecuaciones con ceros de polinomio

• Para un polinomio cuadrático con ceros α y β, el polinomio cuadrático viene dado por

X ² – (a + b)x + ab .

• Para un polinomio cúbico con tres ceros α, β y γ, el polinomio cúbico viene dado por

X ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

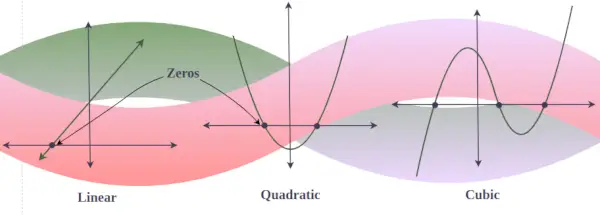
Ceros en gráfica de polinomios

En la gráfica de cualquier polinomio y = f(x), los ceros reales son el punto en el que la gráfica intersecta o toca el eje x. (ya que una gráfica con un cero imaginario nunca corta el eje x). En otras palabras, si hay 3 soluciones reales de un polinomio cúbico, entonces la gráfica de ese polinomio cúbico corta al eje x tres veces, pero si solo hay una solución real para algún polinomio cúbico, entonces la gráfica solo corta al eje x. una vez.

Teorema fundamental del álgebra lineal

Si P(x) es un polinomio de grado n, entonces P(x) tendrá exactamente n ceros, algunos de los cuales pueden repetirse.

Esto significa que si enumeramos todos los ceros y enumeramos cada uno k veces cuando k es su multiplicidad. Tendremos exactamente n números en la lista. Esto puede ser útil ya que nos puede dar una idea de cuántos ceros debe haber en un polinomio. Entonces podemos dejar de buscar ceros una vez que alcancemos el número requerido de ceros.

Multiplicidad de una raíz

Supongamos que tenemos un polinomio P(x) = 0 que se factoriza en,

P(x) = (x – r) ^k (x-a) ^metro

Si r es un cero de un polinomio y el exponente de su término que produjo la raíz es k, entonces decimos que r tiene multiplicidad k . Los ceros con una multiplicidad de 1 a menudo se llaman simple Los ceros y los ceros con multiplicidad de 2 se denominan raíces dobles del polinomio.

Ejemplo: P(x) es un polinomio de grado 5 que ha sido factorizado para usted. Enumera las raíces y su multiplicidad.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x-2) ³

Solución:

Dado, P(x) = 5(x+1)²(x-2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Para encontrar ceros, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Observe que -1 aparece dos veces como cero, por lo que su multiplicidad es 2 mientras que la multiplicidad del cero 2 es 3.

Artículos relacionados con Ceros de Polinomio

• Polinomio
• Raíces de la ecuación cuadrática
• Expresión algebraica

Problemas de muestra sobre ceros de polinomio

Problema 1: Dado que x = 2 es un cero de P(x) = x ³ +2x ² −5x−6. Encuentra los otros dos ceros.

Solución:

Del teorema fundamental que estudiamos anteriormente, podemos decir que P(x) tendrá 3 ceros porque es un polinomio de tres grados. Uno de ellos es x = 2.

Entonces podemos reescribir P(x),

P(x) = (x – 2) Q(x)

Para encontrar los otros dos ceros, necesitamos encontrar Q(x).

Q(x) se puede encontrar dividiendo P(x) por (x-2).

Después de dividir, Q(x) resulta ser,

Q(x) = x²+ 4x + 3

Los dos ceros restantes se pueden encontrar a partir de esto,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Por tanto, los otros dos ceros son x = -1 y x = -3.

Problema 2: Dado que x = r es un cero de un polinomio, encuentra los otros ceros del polinomio.

P(x) = x ³ -6x ² −16x; r = −2

Solución:

Sabemos que x = -2 es cero,

Entonces, P(x) se puede reescribir como P(x) = (x + 2) Q(x) {Usando el algoritmo de división}

Ahora para encontrar Q(x), hacemos lo mismo que hicimos en la pregunta anterior, dividimos P(x) entre (x + 2).

Obtenemos,

Q(x) = x²– 8x

Ahora para encontrar los otros dos ceros, factoriza Q(x)

Q(x) = x (x – 8) = 0

Entonces, los ceros son x = 0, 8.

Por tanto, tenemos tres ceros, x = -2, 0, 8.

Problema 3: Encuentra los ceros del polinomio, 4x ³ -3x ² -25x-6 = 0

Solución:

Truco para resolver ecuaciones polinómicas de grado 3,

Encuentre el número entero más pequeño que pueda hacer que el valor del polinomio sea 0, comience con 1,-1,2, y así sucesivamente...

encontramos que para x = -2 obtenemos que el valor de la expresión sea cero.

Por tanto, una de las raíces es -2.

Según el teorema del factor, si a es uno de los ceros del polinomio, por lo tanto (xa) es el factor del polinomio dado.

Por lo tanto, siguiendo este {x – (-2)} = (x+2) hay un factor pof por encima del polinomio.

Obtenemos una ecuación cuadrática y ya hay ceros.

(4x²-11x-3)(x+2) = 0

Factorizar la ecuación cuadrática,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Problema 4: Encuentra los ceros del polinomio, 4x ⁶ – 16x ⁴ = 0

Solución:

El Polinomio tiene hasta grado 6, por lo tanto, existen 6 ceros del polinomio.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Por lo tanto, x= 0, 0, 0, 0, 2, -2

Problema 5: Encuentra los ceros de la función polinómica f(x) = x ³ – 2x ² – 5x + 6

Solución:

Java público vs privado

Para encontrar los ceros de este polinomio, establecemos f(x) = 0 y resolvemos para x:

f(x) = x³– 2x²– 5x + 6 = 0

Como d/a = 6

Según el teorema de la raíz racional, todas las raíces racionales posibles del polunomio son,

Divisores de d/a = ±1, ±2, ±3, ±6

x = 1, en p(x), obtenemos

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Por tanto, según el teorema del factor, x – 1 es el factor de p(x).

Así, x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Para ceros, p(x) = 0,

Los ceros de p(x) son x = 1, x = -2 y x = 3.

Problemas de práctica sobre ceros de polinomio

1. Encuentra todos los ceros del polinomio f(x) = x ³ – 6x ² + 11x – 6

2. Determina todos los ceros del polinomio g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Encuentra los ceros del polinomio h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Determinar todos los ceros del polinomio. p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Preguntas frecuentes sobre ceros de polinomio

¿Qué son los ceros de un polinomio?

Esos valores reales, porque el valor del polinomio se vuelve 0, es decir, si p(x) es un polinomio y p(a) = 0, entonces x = a es el cero de p(x).

¿Cómo encontrar los ceros de un polinomio?

Existen varios métodos para que varios polinomios diferentes encuentren ceros, como el desglose cuadrático del término medio y la fórmula cuadrática. Para una reordenación lineal simple de variables y para cúbica utilizamos una combinación del teorema de la raíz racional, la división larga, el teorema del factor y el teorema del resto.

¿Puede un polinomio tener más de un cero?

Sí, un polinomio puede tener más de un cero, de hecho, el polinomio de n grados puede tener como máximo n ceros reales.

¿Cuál es la multiplicidad de un cero de un polinomio?

En el proceso de factorización, un factor o un cero de un polinomio luego salió un número de veces un factor o un cero, eso se llama multiplicidad de esa raíz.

¿Cuál es el teorema fundamental del álgebra?

El teorema fundamental del álgebra establece que si P(x) es un polinomio de grado n, entonces P(x) tendrá exactamente n ceros, algunos de los cuales pueden repetirse.

¿Un polinomio de grado n siempre tiene n raíces reales?

No, un polinomio de grado n no siempre tiene n raíces reales, ya que algunas raíces pueden ser números imaginarios o complejos.

¿Cuál es el grado del polinomio cero?

El grado del polinomio cero es cero.