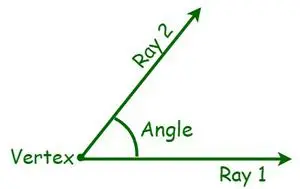
En geometría, un ángulo es una medida esencial de una forma geométrica. Un ángulo se define como el grado de rotación alrededor del punto de intersección entre dos líneas o planos que se requiere para poner una en correspondencia con la otra. Hay varios tipos de ángulos, según la medida de un ángulo. Se mide en términos de grados o radianes. Un ángulo es una forma formada por dos rectas o rayos que divergen de un punto común llamado vértice. Cuando se cruzan dos rayos, es decir, cuando se proyectan medias líneas con un extremo común, se forma un ángulo. Ahora bien, los puntos finales comunes se llaman vértices, mientras que los rayos se conocen como brazos.
Tipos de ángulos

- Ángulo agudo: Un ángulo agudo es un ángulo que tiene más de 0 grados y menos de 90 grados, es decir, oscila entre 0° y 90° (ambos excluyentes).
- Ángulo recto: Se hace referencia a un ángulo recto como el ángulo que mide exactamente 90 grados.
- Ángulo obtuso: Un ángulo obtuso es un ángulo que mide más de 90 grados y menos de 180 grados, es decir, oscila entre 90° y 180° (ambos excluyentes).
- Ángulo recto: Un ángulo llano se conoce como un ángulo que mide exactamente 180 grados.
- Ángulo reflexivo: Un ángulo reflejo es un ángulo que mide más de 180 grados y menos de 360 grados, es decir, oscila entre 180° y 360° (ambos excluyentes).
- Un ángulo completo o Rotación Completa: Se hace referencia a un ángulo completo como aquel que mide exactamente 360 grados.
También existen otros tipos de ángulos, como los ángulos complementarios, los ángulos suplementarios y los ángulos adyacentes y no adyacentes.
- Ángulos complementarios: Se dice que dos ángulos son complementarios si su suma es un ángulo recto, es decir, 90°.
- Ángulos suplementarios: Se dice que dos ángulos son suplementarios si su suma es igual a 180°.
- Ángulos adyacentes: Se dice que dos ángulos son adyacentes si comparten un vértice común y un brazo común.
- Ángulos no adyacentes: Se dice que dos ángulos no son adyacentes si no comparten un vértice común ni un brazo común.
La fórmula para encontrar ángulos
Existen varios tipos de fórmulas para encontrar un ángulo; algunas de ellas son la fórmula del ángulo central, la fórmula del doble ángulo, la fórmula del medio ángulo, la fórmula del ángulo compuesto, la fórmula del ángulo interior, etc.
- Usamos la fórmula del ángulo central para determinar el ángulo de un segmento formado en un círculo.
- Usamos la fórmula de la suma de los ángulos interiores para determinar el ángulo que falta en un polígono.
- Usamos las razones trigonométricas para encontrar el ángulo que falta en un triángulo rectángulo.
- Usamos la ley de los senos o la ley de los cosenos para encontrar el ángulo que falta en un triángulo que no es rectángulo.
Nombre de la Fórmula | Fórmula | ¿Cómo encontrar un ángulo desconocido? |
|---|---|---|
| Fórmula del ángulo central | θ =(s × 360°)/2prAquí, s es la longitud del arco y r es el radio del círculo. | Sustituye los valores de la longitud del arco y el radio del círculo para determinar el ángulo de un segmento formado en un círculo. |
| Fórmula de suma de ángulos interiores | 180°(n-2)donde n es el número de lados de un polígono | Para determinar el ángulo interior desconocido de un polígono, primero calcula la suma de todos los ángulos interiores usando esta fórmula y luego resta la suma de todos los ángulos conocidos del resultado. |
| Razones trigonométricas | sin θ = lado opuesto/hipotenusacos θ = lado adyacente/hipotenusatan θ = lado opuesto/lado adyacente | Dependiendo de los dos lados disponibles de un triángulo rectángulo, elige una de estas razones trigonométricas para encontrar el ángulo desconocido. |
| Ley de los senos | a/sin A = b/sin B = c/sin CAquí A, B y C son los ángulos interiores de un triángulo y a, byc son sus respectivos lados opuestos. | Cuando conocemos dos lados y un ángulo no incluido (o) dos ángulos y un lado no incluido, entonces se puede usar la ley de los senos para determinar los ángulos desconocidos de un triángulo. |
| Ley de cosenos | a2= segundo2+c2– 2bc porque Ab2=c2+ un2– 2ca cos BC2= un2+b2– 2ab porque CAquí A, B y C son los ángulos interiores de un triángulo y a, byc son sus respectivos lados opuestos. | Cuando conocemos tres lados (o) dos lados y un ángulo incluido, entonces se puede usar la ley de los cosenos para determinar los ángulos desconocidos de un triángulo. |
Preguntas de muestra
Pregunta 1: Encuentra el ángulo en el vértice B del triángulo dado usando una de las fórmulas trigonométricas para encontrar ángulos.

Solución:
Dado,
BC = 3 unidades = Lado adyacente de θ.
AC = 4 unidades = Lado opuesto de θ.
En este caso, conocemos tanto el lado opuesto como el lado adyacente de θ. Por tanto, podemos usar la fórmula de la tangente para encontrar θ.
⇒ tan θ = lado opuesto/lado adyacente
⇒ tan θ = 4/3
Java convierte una cadena a un número entero⇒ θ = tan-1(4/3) ⇒ θ = 53,1°
Por tanto, el ángulo en el vértice B es 53,1°.
Pregunta 2: Encuentre los ángulos en los vértices X e Y, si ∠Z = 35° y x = 3 pulgadas, y = 8 pulgadas y z = 3,5 pulgadas.

Solución:
Dado,
∠Z = 35° y x = 6 pulgadas, y = 3 pulgadas y z = 3,5 pulgadas
Como conocemos los tres lados y un ángulo, podemos usar la fórmula de la regla del seno.
De la fórmula de la regla del seno, tenemos
x/sin X = y/ sin Y = z/sin Z
Ahora,
y/ sin Y = z/sin Z
⇒ 3/sin Y = 3.5/sin 35°
⇒ 3/sin Y = 3.5/0.574 {Since, sin 35° = 0.574}
⇒ sin Y = 3 × (0.574/3.5) = 0.492
⇒ ∠Y = sin−1(0.492) = 29.47°
Sabemos que la suma de tres ángulos de un triángulo es 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29.47° + 35° = 180°
⇒ ∠X = 180° – 64.47° = 115.53°
Por lo tanto, ∠X = 115,53° y ∠Y = 29,47°.
Pregunta 3: Calcula el quinto ángulo interior de un pentágono si cuatro de sus ángulos interiores son 110°, 85°, 136° y 105°.
Solución:
El número de lados de un pentágono (n) = 5.
Ahora, la suma de los 5 ángulos interiores de un pentágono = 180 (n -2)°
= 180 (5 – 2)° = 540°.
La suma de los 4 ángulos interiores dados = 110°+ 85°+ 136°+ y 105°= 436°.
decodificar base64 javascriptEntonces, el quinto ángulo interior = 540° – 436° = 104°
Por tanto, el quinto ángulo interior de un pentágono es de 104°.
Pregunta 4: Determina el valor de y y también la medida de los ángulos en la figura dada.

Solución:
De la figura dada, podemos observar que (4y – 6)° y (3y + 5)° son ángulos complementarios, es decir, la suma de (4y – 6)° y (3y + 5)° es 90 °.
⇒ (4y – 6)° + (3y + 5)° = 90°
⇒ (7 años – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Ahora, (4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Pregunta 5: Encuentra el ángulo en el vértice Q en el triángulo dado usando una de las fórmulas para encontrar ángulos.

Solución:
Dado, p = QR = 6 cm, q = PR = 9 cm y r = PQ = 7 cm.
Como conocemos los tres lados y un ángulo, podemos usar la fórmula de la regla del coseno para encontrar el vértice del ángulo Q.
⇒q2=p2+r2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6)(7) porque Q
⇒ 81 = 36 + 49 – 84 porque Q
⇒ 81 = 85 – 84cosQ
⇒84 porque Q = 81 – 85
⇒ 84 porque Q = -4
⇒ porque Q = -4/84 = -1/21
⇒ ∠Q = porque-1(-1/21) = 92.72°
Por tanto, el ángulo en el vértice Q, ∠Q = 92,72°.
Pregunta 6: Calcula el ángulo de un segmento formado en un círculo si la longitud del arco es 12π y el radio es 9 cm.
eres empalme
Solución:
Dado,
La longitud del arco = 12π
Radio (r) = 9 cm
Ahora la fórmula del ángulo es:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
Por tanto, el ángulo es de 240°.
