Volumen de una esfera es la cantidad de líquido que puede contener una esfera. La fórmula del volumen de la esfera se expresa como 4/3πr³. Es el espacio que ocupa una esfera en el espacio tridimensional. Se mide en unidad³es decir m³, cm³, etc. Una esfera es un objeto sólido tridimensional con forma redonda en geometría.

El volumen de la esfera es el espacio total que ocupa la superficie de la esfera y es proporcional al cubo del radio de la esfera. En este artículo, aprenderemos en detalle sobre el volumen de esfera, la fórmula del volumen de esfera, los ejemplos de fórmula del volumen de esfera y otros.

• ¿Qué es el volumen de una esfera?
• Fórmula del volumen de la esfera
• Volumen de una esfera sólida
• Volumen de una esfera hueca
• Derivación de la fórmula del volumen de esfera
• ¿Cómo calcular el volumen de una esfera?

¿Qué es el volumen de una esfera?

El volumen de una esfera es la cantidad de espacio que ocupa dentro de ella. La esfera es una forma sólida, redonda y tridimensional en la que todos los puntos de su superficie están equidistantes de su centro. La distancia fija es el radio de la esfera y el punto fijo es el centro de la esfera. Notaremos un cambio de forma cuando se gire el círculo. Como resultado de la rotación del objeto bidimensional conocido como círculo, se obtiene la forma tridimensional de una esfera.

Aprende más,

• Esfera
• Área de superficie de la esfera

Volumen de una esfera Definición

El volumen de una esfera es la masa total encerrada por la superficie de la esfera. Es el espacio tridimensional dentro de la esfera. Depende del radio de la esfera. La imagen agregada a continuación muestra una esfera de radio r y su volumen.

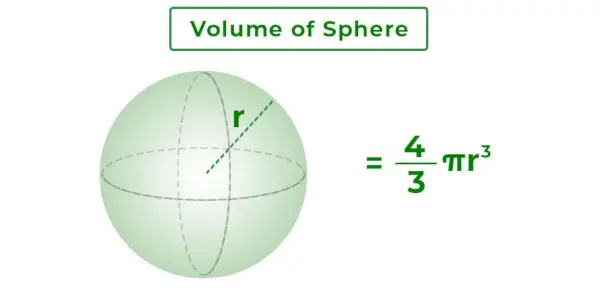
Fórmula del volumen de la esfera

La fórmula del volumen de la esfera es la fórmula que se utiliza para encontrar el volumen de la esfera cuando se da su radio. La fórmula del volumen de esfera para la esfera de radio R se agrega a continuación,

Fórmula del volumen de la esfera = 4/3πr ³

Dónde,

• r es el radio de una esfera
• Pi es una constante y su valor es 22/7

Una esfera generalmente se clasifica en dos que son,

• Volumen de esfera sólida
• Volumen de esfera hueca

Conozcamos sobre ellos en detalle.

Volumen de una esfera sólida

Una esfera sólida es una esfera que está completamente llena hasta el interior. es decir, tiene masa hasta su núcleo y su fórmula para el volumen cuando su radio es r es,

Volumen de una esfera sólida(V) = (4/3)πr ³

Volumen de una esfera hueca

Para una esfera hueca su espacio interno está vacío y supongamos que su radio exterior es R y su radio interior es r, luego su volumen se calcula usando la fórmula,

Volumen de la esfera hueca = (4/3)π(R ³ –r ³ )

Derivación de la fórmula del volumen de esfera

La fórmula del volumen de la esfera se puede derivar utilizando los siguientes métodos:

• Usando la integración
• Usando la relación de Arquímedes entre cilindro, cono y esfera

Analicemos estos métodos en detalle de la siguiente manera:

Volumen de esfera mediante integración

Usando el enfoque de integración, podemos calcular simplemente el volumen de una esfera.

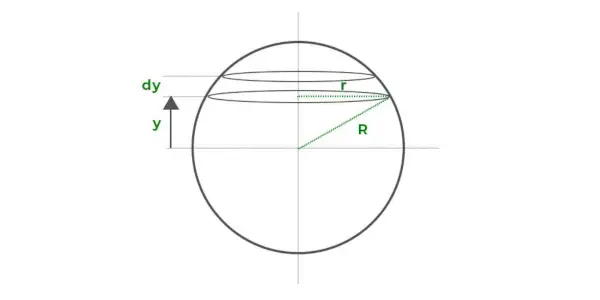
Supongamos que el volumen de la esfera está formado por una serie de discos circulares delgados apilados uno encima del otro, como se muestra en el diagrama de arriba. Cada disco delgado tiene un radio de r y un espesor de dy que está a una distancia y del eje x.

Sea el volumen de un disco dV. El valor de dV viene dado por,

dV = (πr²) tú

Por tanto, dV = π (R²– y²) tú

El volumen total de la esfera será la suma de los volúmenes de todos estos pequeños discos. El valor requerido se puede obtener integrando la expresión del límite -R a R.

Entonces, el volumen de la esfera se convierte en,

V =int_{y=-R}^{y=R} dV

⇒V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒V =pi left[2R^3-frac{2R^3}{3} ight]

⇒V =frac{4}{3}pi R^3

Así, se deriva la fórmula para el volumen de la esfera.

Volumen de esfera usando relaciones de Arquímedes

Como ya demostró Arquímedes, si un cono, una esfera y un cilindro tienen el mismo radio r y la misma altura, sus volúmenes están en la proporción 1:2:3.

Por tanto podemos decir:

Volumen del cilindro = Volumen del cono + Volumen de la esfera

Por lo tanto, Volumen de la Esfera = Volumen del Cilindro – Volumen del Cono

Como sabemos, ese volumen del cilindro = πr²h y volumen del cono = (1/3)πr²h

Sustituyendo estos valores en la ecuación, obtenemos:

Volumen de la esfera = πr²h – (1/3)πr²h = (2/3)πr²h

Suponemos que la altura del cilindro es igual al diámetro de la esfera, que es 2r. De este modo:

El volumen de la esfera es (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Además, consulte

• Fórmula del volumen del casquete esférico
• Fórmula del sector esférico
• Fórmula del segmento esférico

¿Cómo calcular el volumen de una esfera?

El volumen de una esfera es el espacio que ocupa una esfera. Su volumen se puede calcular mediante la fórmula. V = 4/3πr ³ .

Los pasos necesarios para calcular el volumen de una esfera son:

Paso 1: Marca el valor del radio de la esfera.

2 de septiembre: Encuentra el cubo del radio.

Paso 3: Multiplica el cubo del radio por (4/3)π

Etapa 4: Añade la (unidad)³a la respuesta final.

Ejemplo para calcular el volumen de una esfera

Ejemplo: Encuentra el volumen de una esfera con un radio de 7 cm.

Dado, r = 7 cm

V = (4/3)πr³

Volumen de la esfera, V = ((4/3) × π × 7³) cm³

Altura = 1436,8 cm³

Por tanto, el volumen de la esfera es 1436,8 cm.³

Leer más

• Volumen de cono
• Volumen del cubo
• Volumen del cilindro

Ejemplos de volumen de esfera

Ejemplo 1. Encuentra el volumen de la esfera cuyo radio es de 9 cm.

Solución:

Tenemos, r = 9

Volumen de la esfera = 4/3 πr³

⇒ Volumen de la esfera = (4/3) (3,14) (9) (9) (9)

⇒ Volumen de la esfera = (4) (3,14) (3) (9) (9)

⇒ Volumen de la esfera = 3052 cm³

Ejemplo 2. Encuentra el volumen de la esfera cuyo radio es de 12 cm.

Solución:

Tenemos, r = 12

Volumen de la esfera = 4/3 πr³

⇒ Volumen de la esfera = (4/3) (3,14) (12) (12) (12)

⇒ Volumen de la esfera = (4) (3,14) (4) (12) (12)

⇒ Volumen de la esfera = 7234,56 cm³

Ejemplo 3. Encuentra el volumen de la esfera cuyo radio es de 6 cm.

Solución:

Tenemos, r = 6

Volumen de la esfera = 4/3 πr³

⇒ Volumen de la esfera = (4/3) (3,14) (6) (6) (6)

⇒ Volumen de la esfera = (4) (3,14) (2) (6) (6)

⇒ Volumen de la esfera = 904,32 cm³

Ejemplo 4. Encuentra el volumen de la esfera cuyo radio es de 4 cm.

Solución:

Tenemos, r = 4

Volumen de la esfera = 4/3 πr3

⇒ Volumen de la esfera = (4/3) (3,14) (4) (4) (4)

⇒ Volumen de la esfera = (1,33) (3,14) (4) (4) (4)

⇒ Volumen de la esfera = 267,27 cm³

Ejemplo 5. Encuentra el volumen de la esfera cuyo diámetro es de 10 cm.

Solución:

Tenemos, 2r = 10

unix crear directorio

⇒r = 5

Volumen de la esfera = 4/3 πr³

⇒ Volumen de la esfera = (4/3) (3,14) (5) (5) (5)

⇒ Volumen de la esfera = (1,33) (3,14) (5) (5) (5)

⇒ Volumen de la esfera = 522,025 cm³

Ejemplo 6. Encuentra el volumen de la esfera cuyo diámetro es de 16 cm.

Solución:

Tenemos, 2r = 16

⇒r = 8

Volumen de la esfera = 4/3 πr³

⇒ Volumen de la esfera = (4/3) (3,14) (8) (8) (8)

⇒ Volumen de la esfera = (1,33) (3,14) (8) (8) (8)

⇒ Volumen de la esfera = 2138,21 cm³

Ejemplo 7. Encuentra el volumen de la esfera cuyo diámetro es de 14 cm.

Solución:

Tenemos, 2r = 14

⇒r = 7

Volumen de la esfera = 4/3 πr³

⇒ Volumen de la esfera = (4/3) (3,14) (7) (7) (7)

⇒ Volumen de la esfera = (1,33) (3,14) (7) (7) (7)

⇒ Volumen de la esfera = 1432,43 cm³

Volumen de preguntas de práctica de Esfera

P1: Encuentra el volumen de la esfera cuyo diámetro es de 34 cm.

P2: Encuentre el volumen de la esfera hueca cuyo radio interior mide 4 cm y exterior 8 cm.

P3: Encuentra el volumen de la esfera cuyo radio es de 14 cm.

P4: ¿Cuál es el volumen de una esfera cuyo radio es igual al lado de un cuadrado con área de 144 m?².

Volumen de preguntas frecuentes sobre la esfera

¿Qué es el volumen de la esfera?

El volumen de la esfera es el espacio que ocupa la superficie de la esfera.

¿Cuál es la fórmula del área de superficie de una esfera?

El área de superficie total de la esfera de radio r es, Área = 4πr ²

¿Cuál es la fórmula para el volumen de una esfera?

El volumen de una esfera de radio r es, Volumen = 4/3πr ³

¿Cómo encontramos el volumen del hemisferio?

El volumen de un hemisferio de radio r es, Volumen = 2/3πr ³

¿Cuál es la relación entre el volumen de la esfera y el hemisferio?

Si una esfera y un hemisferio tienen el mismo radio, entonces la relación entre sus volúmenes es,

EN ₁ : EN ₂ = (4/3πr ³ ) : (2/3πr ³ ) = 2 : 1

¿Cuál es la unidad de volumen de una esfera?

El volumen de la esfera se mide en m.³, cm³, litros, etc. metro ³ es la unidad de medida estándar.

¿Cuál es el volumen de una esfera cuando su radio se reduce a la mitad?

Volumen de la esfera = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Volumen/8. Entonces el volumen de la esfera es un octavo.