Clasificación topológica para Gráfico acíclico dirigido (DAG) es un ordenamiento lineal de vértices tal que para cada arista dirigida u-v, vértice en viene antes en en el pedido.
Nota: La clasificación topológica de un gráfico no es posible si el gráfico no es un DÍA .
Ejemplo:
Práctica recomendadaSolución basada en DFS para encontrar una clasificación topológica ya se ha discutido.Aporte: Grafico :
Ejemplo
Producción: 5 4 2 3 1 0
Explicación: El primer vértice en la clasificación topológica es siempre un vértice con un grado de entrada de 0 (un vértice sin aristas entrantes). Una clasificación topológica del siguiente gráfico es 5 4 2 3 1 0. Puede haber más de una clasificación topológica para un gráfico. Otra clasificación topológica del siguiente gráfico es 4 5 2 3 1 0.
El orden topológico puede no ser único:
clasificación topológica Es un problema de dependencia en el que la finalización de una tarea depende de la finalización de varias otras tareas cuyo orden puede variar. Entendamos este concepto con un ejemplo:
Supongamos que nuestra tarea es llegar a nuestra escuela y para llegar allí, primero debemos vestirnos. Las dependencias para usar ropa se muestran en el siguiente gráfico de dependencia. Por ejemplo, no puedes usar zapatos antes de usar calcetines.
Por la imagen de arriba ya te habrás dado cuenta de que existen múltiples formas de vestirse, la imagen de abajo muestra algunas de esas formas.
¿Puedes enumerar todo el orden topológico posible de vestirse para el gráfico de dependencia anterior?
10ml a oz
Algoritmo de clasificación topológica mediante DFS:
A continuación se muestra un algoritmo paso a paso para la clasificación topológica mediante la búsqueda en profundidad (DFS):
kajal agarwal
- Crea un gráfico con norte vértices y metro -bordes dirigidos.
- Inicializar una pila y una matriz de tamaño visitada norte .
- Para cada vértice no visitado del gráfico, haga lo siguiente:
- Llame a la función DFS con el vértice como parámetro.
- En la función DFS, marque el vértice como visitado y llame recursivamente a la función DFS para todos los vecinos no visitados del vértice.
- Una vez que se hayan visitado todos los vecinos, empuje el vértice hacia la pila.
- Después de todo, se han visitado los vértices, extraiga elementos de la pila y agréguelos a la lista de salida hasta que la pila esté vacía.
- La lista resultante es el orden topológico del gráfico.
Ilustración del algoritmo de clasificación topológica:
La siguiente imagen es una ilustración del enfoque anterior:

Flujo de trabajo general de clasificación topológica
Paso 1:
- Iniciamos DFS desde el nodo 0 porque no tiene ningún nodo entrante.
- Empujamos el nodo 0 en la pila y pasamos al siguiente nodo que tiene un número mínimo de nodos adyacentes, es decir, el nodo 1.
Paso 2:
- En este paso, debido a que no hay ningún adyacente a este nodo, empuje el nodo 1 en la pila y pase al siguiente nodo.
Paso 3:
- En este paso, elegimos el nodo 2 porque tiene un número mínimo de nodos adyacentes después de 0 y 1.
- Llamamos a DFS para el nodo 2 y empujamos todos los nodos que atraviesan el nodo 2 en orden inverso.
- Entonces presione 3 y luego presione 2.
Etapa 4:
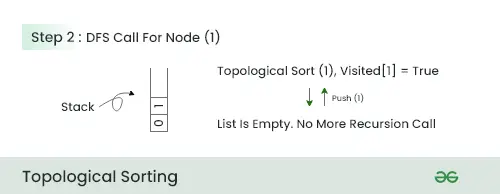
- Ahora llamamos a DFS para el nodo 4.
- Debido a que 0 y 1 ya están presentes en la pila, simplemente empujamos el nodo 4 en la pila y regresamos.
Paso 5:
- En este paso, debido a que todos los nodos adyacentes de 5 ya están en la pila, empujamos el nodo 5 en la pila y regresamos.
Paso 6: Este es el paso final de la clasificación topológica en el que sacamos todos los elementos de la pila y los imprimimos en ese orden.
A continuación se muestra la implementación del enfoque anterior:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vector & visitado, pila & Stack) { // Marcar el nodo actual como visitado visitado[v] = true; // Recurre para todos los vértices adyacentes for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Empuja el vértice actual a la pila que almacena el resultado Stack.push(v); } // Función para realizar la clasificación topológica void topologicalSort(vector>& adj, int V) { pila Pila; // Pila para almacenar el vector de resultados visitado(V, falso); // Llame a la función auxiliar recursiva para almacenar // Orden topológico comenzando desde todos los vértices uno por // uno para (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> bordes = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Gráfico representado como un vector de lista de adyacencia> adj(V); for (auto i: bordes) { adj[i[0]].push_back(i[1]); } escucha<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, booleano[] visitado, Pila pila) { // Marcar el nodo actual como visitado visitado[v] = true; // Recurre para todos los vértices adyacentes for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Empuja el vértice actual a la pila que almacena el // resultado stack.push(v); } // Función para realizar la clasificación topológica static void topologicalSort(List> adj, int V) { // Pila para almacenar el resultado Pila pila = nueva pila(); booleano[] visitado = nuevo booleano[V]; // Llame a la función auxiliar recursiva para almacenar // Orden topológico comenzando desde todos los vértices uno // por uno para (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> bordes = nueva ArrayList(); bordes.add(Arrays.asList(0, 1)); bordes.add(Arrays.asList(1, 2)); bordes.add(Arrays.asList(3, 1)); bordes.add(Arrays.asList(3, 2)); // Gráfico representado como una lista de adyacencia Lista> adj = nueva ArrayList(V); para (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List yo: bordes) { adj.get(i.get(0)).add(i.get(1)); } ordenación topológica(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] visitado, Pila pila) { // Marcar el nodo actual como visitado visitado[v] = true; // Recurre para todos los vértices adyacentes foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Empuja el vértice actual a la pila que almacena el // resultado stack.Push(v); } // Función para realizar la clasificación topológica static void TopologicalSort(List> adj, int V) { // Pila para almacenar el resultado Pila pila = nueva pila (); bool[] visitado = nuevo bool[V]; // Llame a la función auxiliar recursiva para almacenar // Orden topológico comenzando desde todos los vértices uno // por uno para (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Consola.Write(stack.Pop() + ' '); } } // Código del controlador static void Main(string[] args) { // Número de nodos int V = 4; // Lista de bordes> bordes = nueva lista>{ nueva lista { 0, 1 }, nueva lista { 1, 2 }, nueva lista { 3, 1 }, nueva lista { 3, 2 } }; // Gráfico representado como una lista de adyacencia Lista> adj = nueva lista>(); para (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Lista i en bordes) { adj[i[0]].Add(i[1]); } Ordenación topológica(adj, V); } }>
JavaScript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Código del controlador (() => { // Número de nodos constante V = 4; // Bordes constantes bordes = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Gráfico representado como una lista de adyacencia const adj = Array.from({ length: V }, () => []); (i[1]); } ordenación topológica(adj, V })();> Producción
Topological sorting of the graph: 3 0 1 2>
Complejidad del tiempo: O(V+E). El algoritmo anterior es simplemente DFS con una pila adicional. Entonces la complejidad del tiempo es la misma que la de DFS.
Espacio auxiliar: O(V). Se necesita espacio adicional para la pila.
Clasificación topológica mediante BFS:
recorrido del árbolC++
#include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Puntero a una matriz que contiene // listas de adyacencia public: Graph(int V); // Constructor void addEdge(int v, int w); // Función para agregar un borde al gráfico void topologicalSort(); // imprime un tipo topológico de // el gráfico completo }; Gráfico::Gráfico(int V) { this->V = V; adj = nueva lista [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Agrega w a la lista de v. } // Función para realizar la clasificación topológica void Graph::topologicalSort() { // Crea un vector para almacenar el grado de entrada de todos los vectores de vértices en_grado(V, 0); // Recorrer listas de adyacencia para completar in_grado de // vértices para (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; para (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector orden_superior; // Uno por uno retira los vértices de la cola y los pone en cola // vértices adyacentes si el grado de adyacente se convierte en 0 while (!q.empty()) { // Extrae el frente de la cola (o realiza la retirada de la cola) // y agrégalo a orden topológico int u = q.front(); q.pop(); top_order.push_back(u); // Iterar a través de todos sus nodos vecinos // del nodo u retirado de la cola y disminuir su grado de entrada // en 1 lista ::iterador itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Si el grado se vuelve cero, agréguelo a la cola if (--in_grado[*itr ] == 0) q.push(*itr); contar++; } // Comprobar si hubo un ciclo if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Lista de adyacencia // representación de // el gráfico // Constructor Graph(int V) { this.V = V; adj = nueva ListaArray[V]; para (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = nueva ListaEnlazada(); para (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList ordensuperior = nueva ArrayList(); // Uno por uno retira los vértices de la cola y // pone en cola los vértices adyacentes si el grado de // adyacente se convierte en 0 while (!q.isEmpty()) { // Extrae el frente de la cola y agrégalo al // orden topológico int u = q.encuesta(); topOrder.add(u); contar++; // Iterar a través de todos sus nodos vecinos del // nodo u retirado de la cola y disminuir su grado de entrada // en 1 for (int w : adj[u]) { // Si el grado de entrada se vuelve cero, agréguelo a // la cola if (--inDegree[w] == 0) q.add(w); } } // Comprobar si hubo un ciclo if (count != V) { System.out.println('El gráfico contiene el ciclo'); devolver; } // Imprimir orden topológico para (int i: topOrder) System.out.print(i + ' '); } } // Código del controlador public class Main { public static void main(String[] args) { // Crea un gráfico dado en el diagrama anterior Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Lo siguiente es un tipo topológico del gráfico dado'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> javascript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Producción
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
Complejidad del tiempo:
La complejidad temporal para construir el gráfico es O (V + E), donde V es el número de vértices y E es el número de aristas.
La complejidad temporal para realizar la clasificación topológica utilizando BFS también es O (V + E), donde V es el número de vértices y E es el número de aristas. Esto se debe a que cada vértice y cada arista se visita una vez durante el recorrido BFS.
Complejidad espacial:
La complejidad espacial para almacenar el gráfico usando una lista de adyacencia es O (V + E), donde V es el número de vértices y E es el número de aristas.
Se utiliza espacio adicional para almacenar el grado de entrada de los vértices, lo que requiere espacio O(V).
Se utiliza una cola para el recorrido BFS, que puede contener como máximo V vértices. Por tanto, la complejidad espacial de la cola es O(V).
En general, la complejidad espacial del algoritmo es O (V + E) debido al almacenamiento del gráfico, la matriz en grados y la cola.
En resumen, la complejidad temporal de la implementación proporcionada es O (V + E), y la complejidad espacial también es O (V + E).
Nota: Aquí también podemos usar una matriz en lugar de una pila. Si se utiliza la matriz, imprima los elementos en orden inverso para obtener la clasificación topológica.
Ventajas de la clasificación topológica:
- Ayuda a programar tareas o eventos basados en dependencias.
- Detecta ciclos en un gráfico dirigido.
- Eficiente para resolver problemas con restricciones de precedencia.
Desventajas del ordenamiento topológico:
- Solo aplicable a gráficos acíclicos dirigidos (DAG), no apto para gráficos cíclicos.
- Puede no ser único, pueden existir múltiples ordenamientos topológicos válidos.
- Ineficiente para gráficos grandes con muchos nodos y aristas.
Aplicaciones de ordenación topológica:
- Programación de tareas y gestión de proyectos.
- Resolución de dependencias en sistemas de gestión de paquetes.
- Determinar el orden de compilación en sistemas de construcción de software.
- Detección de interbloqueos en sistemas operativos.
- Programación de cursos en las universidades.
Artículos relacionados:
- Algoritmo de Kahn para la clasificación topológica
- Todos los tipos topológicos de un gráfico acíclico dirigido