En este artículo, discutiremos el recorrido del árbol en la estructura de datos. El término 'recorrido de árbol' significa atravesar o visitar cada nodo de un árbol. Existe una única forma de atravesar la estructura de datos lineal, como lista vinculada, cola y pila. Considerando que existen varias formas de atravesar un árbol que se enumeran a continuación:
- recorrido de preorden
- recorrido en orden
- Recorrido del giro postal
Entonces, en este artículo, discutiremos las técnicas mencionadas anteriormente para atravesar un árbol. Ahora, comencemos a discutir las formas de atravesar árboles.
recorrido de preorden
Esta técnica sigue la política de 'raíz izquierda derecha'. Significa que se visita el primer nodo raíz, luego se recorre recursivamente el subárbol izquierdo y, finalmente, se recorre recursivamente el subárbol derecho. Como el nodo raíz se atraviesa antes (o antes) de los subárboles izquierdo y derecho, se denomina recorrido de preorden.
Entonces, en un recorrido de preorden, cada nodo se visita antes que sus dos subárboles.
Las aplicaciones del recorrido de preorden incluyen:
- Se utiliza para crear una copia del árbol.
- También se puede utilizar para obtener la expresión de prefijo de un árbol de expresión.
Algoritmo
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Ejemplo
Ahora, veamos el ejemplo de la técnica transversal de preorden.
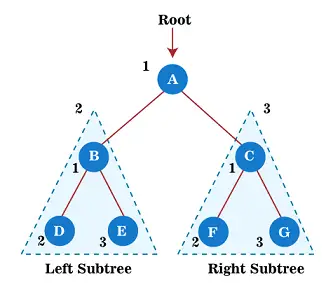
Ahora, comience a aplicar el recorrido de preorden en el árbol de arriba. Primero, atravesamos el nodo raíz. A; después de eso, muévase a su subárbol izquierdo B , que también se recorrerá en preorden.
Entonces, para el subárbol izquierdo B, primero, el nodo raíz B se atraviesa a sí mismo; después de eso, su subárbol izquierdo D es atravesado. desde nodo D no tiene hijos, muévase al subárbol derecho Y . Como el nodo E tampoco tiene hijos, se completa el recorrido del subárbol izquierdo del nodo raíz A.
np.dónde
Ahora, muévase hacia el subárbol derecho del nodo raíz A, que es C. Entonces, para el subárbol derecho C, primero el nodo raíz C se ha atravesado a sí mismo; después de eso, su subárbol izquierdo F es atravesado. desde nodo F no tiene hijos, muévase al subárbol derecho GRAMO . Como el nodo G tampoco tiene hijos, se completa el recorrido del subárbol derecho del nodo raíz A.
Por tanto, se atraviesan todos los nodos del árbol. Entonces, el resultado del recorrido de preorden del árbol anterior es:
A → B → D → E → C → F → G
Para saber más sobre el recorrido del pedido anticipado en la estructura de datos, puede seguir el enlace recorrido de preorden .
Recorrido del giro postal
Esta técnica sigue la política de 'raíz izquierda-derecha'. Significa que se atraviesa el primer subárbol izquierdo del nodo raíz, luego se atraviesa recursivamente el subárbol derecho y, finalmente, se atraviesa el nodo raíz. A medida que el nodo raíz se recorre después (o después) de los subárboles izquierdo y derecho, se denomina recorrido posterior al orden.
Entonces, en un recorrido de postorden, cada nodo se visita después de sus dos subárboles.
multiplexación
Las aplicaciones del recorrido posterior al orden incluyen:
- Se utiliza para eliminar el árbol.
- También se puede utilizar para obtener la expresión postfija de un árbol de expresión.
Algoritmo
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Ejemplo
Ahora, veamos el ejemplo de la técnica transversal de postorden.

Ahora, comience a aplicar el recorrido de postorden en el árbol de arriba. Primero, atravesamos el subárbol izquierdo B que se recorrerá en orden posterior. Después de eso, atravesaremos el subárbol derecho. C en postorden. Y finalmente, el nodo raíz del árbol anterior, es decir, A , es atravesado.
anaconda vs serpiente pitón
Entonces, para el subárbol izquierdo B, primero, su subárbol izquierdo D es atravesado. desde nodo D no tiene hijos, atraviesa el subárbol derecho Y . Como el nodo E tampoco tiene hijos, muévase al nodo raíz B. Después de atravesar el nodo B, se completa el recorrido del subárbol izquierdo del nodo raíz A.
Ahora, muévase hacia el subárbol derecho del nodo raíz A, que es C. Entonces, para el subárbol derecho C, primero su subárbol izquierdo F es atravesado. desde nodo F no tiene hijos, atraviesa el subárbol derecho GRAMO . Como el nodo G tampoco tiene hijos, finalmente, el nodo raíz del subárbol derecho, es decir, C, es atravesado. Se completa el recorrido del subárbol derecho del nodo raíz A.
Por último, recorra el nodo raíz de un árbol determinado, es decir, A . Después de atravesar el nodo raíz, se completa el recorrido posterior al orden del árbol dado.
Por tanto, se atraviesan todos los nodos del árbol. Entonces, el resultado del recorrido posterior al orden del árbol anterior es:
D → E → B → F → G → C → A
Para saber más sobre el recorrido posterior al pedido en la estructura de datos, puede seguir el enlace Recorrido del giro postal .
recorrido en orden
Esta técnica sigue la política de 'raíz izquierda derecha'. Significa que se visita el primer subárbol izquierdo después de atravesar el nodo raíz y, finalmente, se atraviesa el subárbol derecho. A medida que el nodo raíz se atraviesa entre los subárboles izquierdo y derecho, se denomina recorrido en orden.
Entonces, en el recorrido en orden, cada nodo se visita entre sus subárboles.
Las aplicaciones del recorrido en orden incluyen:
- Se utiliza para obtener los nodos BST en orden creciente.
- También se puede utilizar para obtener la expresión de prefijo de un árbol de expresión.
Algoritmo
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Ejemplo
Ahora, veamos el ejemplo de la técnica transversal Inorder.

Ahora, comience a aplicar el recorrido en orden en el árbol de arriba. Primero, atravesamos el subárbol izquierdo. B que se recorrerá en orden. Después de eso, atravesaremos el nodo raíz. A . Y finalmente, el subárbol derecho. C se recorre en orden.
Entonces, para el subárbol izquierdo B , primero, su subárbol izquierdo D es atravesado. desde nodo D no tiene hijos, así que después de atravesarlo, el nodo B será atravesado, y por último, el subárbol derecho del nodo B, es decir Y , es atravesado. El nodo E tampoco tiene hijos; por lo tanto, se completa el recorrido del subárbol izquierdo del nodo raíz A.
Después de eso, atraviesa el nodo raíz de un árbol determinado, es decir, A .
Por último, avance hacia el subárbol derecho del nodo raíz A, que es C. Entonces, para el subárbol derecho C; primero, su subárbol izquierdo F es atravesado. desde nodo F no tiene hijos, nodo C será atravesado, y por último, un subárbol derecho del nodo C, es decir, GRAMO , es atravesado. El nodo G tampoco tiene hijos; por lo tanto, se completa el recorrido del subárbol derecho del nodo raíz A.
A medida que se atraviesan todos los nodos del árbol, se completa el recorrido en orden del árbol dado. El resultado del recorrido en orden del árbol anterior es:
D → B → E → A → F → C → G
Para saber más sobre el recorrido en orden en la estructura de datos, puede seguir el enlace Recorrido en orden .
java reemplaza el carácter en la cadena
Complejidad de las técnicas de recorrido de árboles.
La complejidad temporal de las técnicas de recorrido de árboles discutidas anteriormente es En) , dónde 'norte' es el tamaño del árbol binario.
Mientras que la complejidad espacial de las técnicas de recorrido de árboles discutidas anteriormente es O(1) si no consideramos el tamaño de la pila para las llamadas a funciones. De lo contrario, la complejidad espacial de estas técnicas es Oh) , dónde 'h' es la altura del árbol.
Implementación del recorrido del árbol.
Ahora, veamos la implementación de las técnicas discutidas anteriormente utilizando diferentes lenguajes de programación.
Programa: Escriba un programa para implementar técnicas de recorrido de árboles en C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Producción

Programa: Escriba un programa para implementar técnicas de recorrido de árboles en C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Producción

Programa: Escriba un programa para implementar técnicas de recorrido de árboles en C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Producción
java compareto
Después de la ejecución del código anterior, el resultado será:

Conclusión
En este artículo, hemos analizado los diferentes tipos de técnicas de recorrido de árboles: recorrido en preorden, recorrido en orden y recorrido en postorden. Hemos visto estas técnicas junto con algoritmos, ejemplos, complejidad e implementación en C, C++, C# y Java.
Entonces, eso es todo sobre el artículo. Espero que te resulte útil e informativo.
