Fórmulas sen cos en trigonometría: La trigonometría, como su nombre lo indica, es el estudio de los triángulos. Es una rama importante de las matemáticas que estudia la relación entre las longitudes de los lados y los ángulos del triángulo rectángulo y también ayuda a determinar las longitudes de los lados o ángulos que faltan en un triángulo. Hay seis razones o funciones trigonométricas: seno, coseno, tangente, cosecante, secante y cotangente, donde cosecante, secante y cotangente son las funciones recíprocas de las otras tres funciones, es decir, seno, coseno y tangente, respectivamente.
Una razón trigonométrica se define como la razón de las longitudes de los lados de un triángulo rectángulo. La trigonometría se emplea en diversos campos de nuestra vida diaria. Ayuda a determinar las alturas de colinas o edificios. También se utiliza en campos como criminología, construcción, física, arqueología, ingeniería de motores marinos, etc.
En este artículo, exploraremos todos Fórmulas de trigonometría, en su mayoría fórmulas de seno y cos con sus ejemplos, y una lista de todas las fórmulas de trigonometría.
Tabla de contenidos
- Fórmulas en trigonometría
- Algunas fórmulas básicas de pecado y cos
- Sin Cos Formulas Table
- Sin Cos Formulas Examples
- Problemas de práctica sobre fórmulas sen cos en trigonometría con ejemplos
Fórmulas en trigonometría
Consideremos un triángulo rectángulo XYZ, donde ∠Y = 90°. Sea θ el ángulo en el vértice Z. El lado adyacente a θ se llama lado adyacente y el lado opuesto a θ se llama lado opuesto. Una hipotenusa es un lado opuesto al ángulo recto o al lado más largo de un ángulo recto.
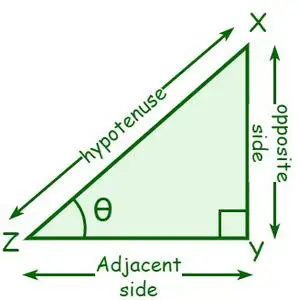
- sin θ = lado opuesto/hipotenusa
- cos θ = Lado adyacente/Hipotenusa
- tan θ = Lado opuesto/Lado adyacente
- cosec θ = 1/sen θ = Hipotenusa/Lado opuesto
- sec θ = 1/ cos θ = hipotenusa/lado adyacente
- cot θ = 1/ tan θ = Lado adyacente/Lado opuesto
Fórmula seno
El seno de un ángulo en un triángulo rectángulo es la razón entre la longitud del lado opuesto y la longitud de la hipotenusa del ángulo dado. Una función seno se representa como pecado.
sin θ = lado opuesto/hipotenusa
Fórmula del coseno
El coseno de un ángulo en un triángulo rectángulo es la razón entre la longitud del lado adyacente y la longitud de la hipotenusa del ángulo dado. Una función coseno se representa como cos.
seleniocos θ = Lado adyacente/Hipotenusa
Algunas fórmulas básicas de pecado y cos
Funciones seno y coseno en cuadrantes
- La función seno es positiva en el primer y segundo cuadrante y negativa en el tercero y cuarto cuadrante.
- La función coseno es positiva en el primer y cuarto cuadrante y negativa en el segundo y tercer cuadrante.
Grados
Cuadrante
Signo de la función seno
Signo de la función coseno
0° a 90°
1er cuadrante
+ (positivo)
+ (positivo)
90° a 180°
2do cuadrante
+ (positivo)
- (negativo)
180° a 270°
3er cuadrante
- (negativo)
- (negativo)
270° a 360°
4to cuadrante
- (negativo)
+ (positivo)
La identidad de los ángulos negativos de las funciones seno y coseno.
- El seno de un ángulo negativo siempre es igual al seno negativo del ángulo.
pecado (– θ) = – pecado θ
- El coseno de un ángulo negativo siempre es igual al coseno del ángulo.
porque (– θ) = porque θ
Relación entre la función seno y coseno
sen θ = cos (90° – θ)
Funciones recíprocas de las funciones seno y coseno
- Una función cosecante es la función recíproca de la función seno.
cosec θ = 1/sen θ
- Una función secante es la función recíproca de la función coseno.
seg θ = 1/cos θ
Identidad pitagórica
sin 2 θ + porque 2 θ = 1
Identidades periódicas de las funciones seno y coseno.
pecado (θ + 2nπ) = pecado θ
porque (θ + 2nπ) = porque θ
Fórmulas de doble ángulo para las funciones seno y coseno
sen 2θ = 2 sen θ cos θ
porque 2θ = porque 2 θ – pecado 2 θ = 2 porque 2 θ – 1 = 1 – 2 pecado 2 i
Identidades de semiángulos para las funciones seno y coseno
pecado (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Identidades de ángulos triples para las funciones seno y coseno
pecado 3θ = 3 pecado θ – 4 pecado 3 i
porque 3θ = 4cos 3 θ – 3 porque θ
Fórmulas de suma y diferencia.
- función seno
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- función coseno
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Ley de los senos o regla del seno
La ley de los senos de la regla del seno es una ley trigonométrica que proporciona una relación entre las longitudes de los lados y los ángulos de un triángulo.

a/sin A = b/sin B = c/sin C
Donde a, byc son las longitudes de los tres lados del triángulo ABC, y A, B y C son los ángulos.
Ley de cosenos
La ley de los cosenos de la regla del coseno se utiliza para determinar los ángulos o longitudes de los lados faltantes o desconocidos de un triángulo.

a 2 = segundo 2 +c 2 – 2bc porque A
b 2 =c 2 + un 2 – 2ca cos B
C 2 = un 2 +b 2 – 2ab porque C
Donde a, byc son las longitudes de los tres lados del triángulo ABC, y A, B y C son los ángulos.
Sin Cos Formulas Table
Aquí está la tabla/lista de fórmulas de seno y cos para varios ángulos en grados y radianes:
Lista de fórmulas de seno y cos
| Ángulo (en grados) | Ángulo (en radianes) | pecado yo | porque θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Sin Cos Formulas Examples
Problema 1: Si cos α = 24/25, entonces encuentre el valor de sen α.
Solución:
Dado,
porque α = 24/25
De las identidades pitagóricas tenemos;
porque2θ + pecado2θ = 1
(24/25)2+ sin2a = 1
sin2α = 1 – (24/25)2
sin2α = 1 – (576/625) = (625 – 576)/625
sin2α = (625 – 576)/625 = 49/626
sen α = √49/625 = ±7/25
Por tanto, sen α = ±7/25.
Problema 2: Demuestre las fórmulas de sen 2A y cos 2A, si ∠A= 30°.
Solución:
Dado, ∠A= 30°
Lo sabemos,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Since, sin 30° = 1/2, cos 30° = √3/2 and sin 60° = √3/2}
√3/2 = √3/2
LHS = RHS
2) porque 2A = 2cos2A – 1
porque 2(30°) = 2cos2(30°) – 1
porque 60° = 2(√3/2)2– 1 = 3/2 – 1 {Ya que, cos 60° = 1/2 y cos 30° = √3/2}
reemplazar todo java1/2 = 1/2
LHS = RHS
Por lo tanto demostrado.
Problema 3: Encuentra el valor de cos x, si tan x = 3/4.
Solución:
Dado, tan x = 3/4
Lo sabemos,
tan x = lado opuesto/lado adyacente = 3/4
Para encontrar la hipotenusa usamos el teorema de Pitágoras:
hipotenusa2= opuesto2+ adyacente2
h2= 32+ 42
h2= 9 + 16 = 25
H = √25 = 5
Ahora, cos x = lado adyacente/hipotenusa
cos x = 4/5
Por tanto, el valor de cos x es 4/5.
Problema 4: Encuentre ∠C (en grados) y ∠A (en grados), si ∠B = 45°, BC = 15 pulgadas y AC = 12 pulgadas.

Solución:
Dado: ∠B = 45°, BC = a = 15 pulgadas y AC = b = 12 pulgadas.
De la ley de los senos tenemos
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16.97
⇒ sin A = 15/16.97 = 0.8839
⇒ ∠A = sin-1(0.8839) = 62.11°
Sabemos que la suma de los ángulos internos de un triángulo es 180°.
Entonces, ∠A + ∠B + ∠C = 180°
⇒ 62.11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62.11° + 45°) = 72.89°
Por lo tanto, ∠A = 62,11° y ∠C = 72,89°.
Problema 5: Demuestre las identidades de los semiángulos de la función coseno.
Solución:
La identidad del semiángulo de la función coseno es:
cos (θ/2) = ±√[(1 + cos θ)/2]
A partir de identidades de doble ángulo, tenemos,
cos 2A = 2 cos2A – 1
Ahora reemplaza A con θ/2 en ambos lados
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ porque2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Por lo tanto demostrado.
Problemas de práctica sobre fórmulas sen cos en trigonometría con ejemplos
1. Dado sen θ = 3/5. Encuentre cos θ.
2. Demuestre la identidad sin(2A) = 2 sinA cosA para A=45∘.
3. Si cos α = 5/13. Encuentra el pecado (2a).
4. Resuelva para θ si sin θ = cos(90∘−θ).
5. Si tan β = 2. Encuentra sen β y cos β usando la identidad pitagórica.
Preguntas frecuentes sobre fórmulas sen cos en trigonometría con ejemplos
¿Cuáles son las fórmulas básicas de seno y coseno en trigonometría?
Las fórmulas básicas de seno y coseno son sin θ = Opuesto/Hipotenusa y cos θ = Adyacente/Hipotenusa, donde θ es un ángulo en un triángulo rectángulo.
¿Cómo encuentras el seno y el coseno de ángulos especiales?
Ángulos especiales como 0∘, 30∘, 45∘, 60∘ y 90∘ tienen valores de seno y coseno específicos que se pueden recordar usando tablas trigonométricas o conceptos de círculo unitario.
¿Cuál es la relación entre las funciones seno y coseno?
Las funciones seno y coseno están relacionadas por la identidad pecado θ = cos(90∘- θ) y la identidad pitagórica sin 2 θ+cos 2 θ = 1.
¿Cómo se utilizan las fórmulas de los ángulos dobles para el seno y el coseno?
Las fórmulas de los dobles ángulos son sin(2θ) = 2sinθcosθ y porque(2θ)=cos 2 θ – pecado 2 i. Se utilizan para expresar funciones trigonométricas de ángulos dobles en términos de ángulos simples.
¿Cómo encuentras los valores del seno y el coseno para ángulos en diferentes cuadrantes?
Los signos de las funciones seno y coseno dependen del cuadrante en el que se encuentra el ángulo:
- Primer cuadrante: sen θ> 0 y cos θ> 0
- Segundo cuadrante: sen θ> 0 y cos θ <0
- Tercer cuadrante: sinθ <0 y cosθ < 0
- Cuarto cuadrante: senθ 0
