El gráfico cuantil-cuantil (gráfico q-q) es un método gráfico para determinar si un conjunto de datos sigue una determinada distribución de probabilidad o si dos muestras de datos provienen del mismo población O no. Los gráficos Q-Q son particularmente útiles para evaluar si un conjunto de datos es Normalmente distribuido o si sigue alguna otra distribución conocida. Se utilizan comúnmente en estadística, análisis de datos y control de calidad para verificar suposiciones e identificar desviaciones de las distribuciones esperadas.
Cuantiles y percentiles
Los cuantiles son puntos en un conjunto de datos que dividen los datos en intervalos que contienen probabilidades o proporciones iguales de la distribución total. A menudo se utilizan para describir la extensión o distribución de un conjunto de datos. Los cuantiles más comunes son:
- Mediana (percentil 50) : La mediana es el valor medio de un conjunto de datos cuando se ordena de menor a mayor. Divide el conjunto de datos en dos mitades iguales.
- Cuartiles (percentiles 25, 50 y 75) : Los cuartiles dividen el conjunto de datos en cuatro partes iguales. El primer cuartil (Q1) es el valor por debajo del cual cae el 25% de los datos, el segundo cuartil (Q2) es la mediana y el tercer cuartil (Q3) es el valor por debajo del cual cae el 75% de los datos.
- percentiles : Los percentiles son similares a los cuartiles pero dividen el conjunto de datos en 100 partes iguales. Por ejemplo, el percentil 90 es el valor por debajo del cual cae el 90% de los datos.
Nota:
- Un gráfico q-q es un gráfico de los cuantiles del primer conjunto de datos frente a los cuantiles del segundo conjunto de datos.
- Como referencia, también se traza una línea del 45%; Para si las muestras son de la misma población, entonces los puntos están a lo largo de esta línea.
Distribución normal:
La distribución normal (también conocida como curva de Bell de distribución gaussiana) es una distribución de probabilidad continua que representa la distribución obtenida a partir de valores reales generados aleatoriamente.
. 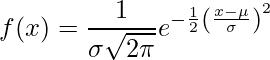

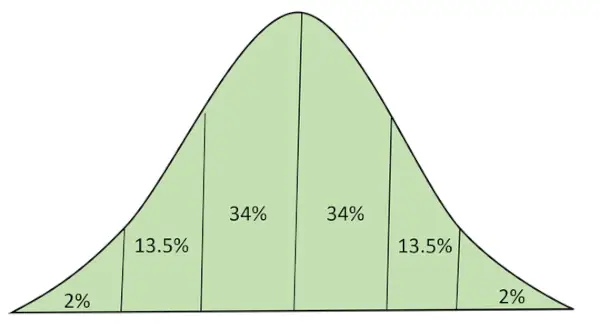
Distribución normal con área bajo curva
¿Cómo dibujar el diagrama Q-Q?
Para dibujar un gráfico cuantil-cuantil (Q-Q), puede seguir estos pasos:
- Recopilar los datos : recopile el conjunto de datos para el que desea crear el gráfico Q-Q. Asegúrese de que los datos sean numéricos y representen una muestra aleatoria de la población de interés.
- Ordenar los datos : organiza los datos en orden ascendente o descendente. Este paso es esencial para calcular los cuantiles con precisión.
- Elija una distribución teórica : determine la distribución teórica con la que desea comparar su conjunto de datos. Las opciones comunes incluyen la distribución normal, la distribución exponencial o cualquier otra distribución que se ajuste bien a sus datos.
- Calcular cuantiles teóricos : Calcule los cuantiles de la distribución teórica elegida. Por ejemplo, si compara con una distribución normal, usaría la función de distribución acumulativa inversa (CDF) de la distribución normal para encontrar los cuantiles esperados.
- Graficado :
- Trazar los valores del conjunto de datos ordenados en el eje x.
- Trace los cuantiles teóricos correspondientes en el eje y.
- Cada punto de datos (x, y) representa un par de valores observados y esperados.
- Conecte los puntos de datos para inspeccionar visualmente la relación entre el conjunto de datos y la distribución teórica.
Interpretación del gráfico Q-Q
- Si los puntos en el gráfico caen aproximadamente a lo largo de una línea recta, sugiere que su conjunto de datos sigue la distribución supuesta.
- Las desviaciones de la línea recta indican desviaciones de la distribución supuesta, lo que requiere más investigación.
Explorando la similitud de distribución con gráficos Q-Q
Explorar la similitud de distribución utilizando gráficos Q-Q es una tarea fundamental en estadística. Comparar dos conjuntos de datos para determinar si se originan en la misma distribución es vital para diversos fines analíticos. Cuando se cumple el supuesto de una distribución común, la combinación de conjuntos de datos puede mejorar la precisión de la estimación de parámetros, como la ubicación y la escala. Los gráficos Q-Q, abreviatura de gráficos cuantiles-cuantiles, ofrecen un método visual para evaluar la similitud de distribución. En estos gráficos, los cuantiles de un conjunto de datos se comparan con los cuantiles de otro. Si los puntos se alinean estrechamente a lo largo de una línea diagonal, sugiere similitud entre las distribuciones. Las desviaciones de esta línea diagonal indican diferencias en las características de distribución.
Mientras que pruebas como la chi-cuadrado y Kolmogorov-Smirnov Las pruebas pueden evaluar las diferencias generales de distribución, los gráficos Q-Q proporcionan una perspectiva matizada al comparar directamente cuantiles. Esto permite a los analistas discernir diferencias específicas, como cambios de ubicación o cambios de escala, que pueden no ser evidentes únicamente a partir de pruebas estadísticas formales.
Implementación en Python del gráfico Q-Q
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Producción:
Trama QQ
Aquí, como los puntos de datos siguen aproximadamente una línea recta en el gráfico Q-Q, sugiere que el conjunto de datos es consistente con la distribución teórica asumida, que en este caso asumimos que es la distribución normal.
Ventajas del gráfico Q-Q
- Comparación flexible : Los gráficos Q-Q pueden comparar conjuntos de datos de diferentes tamaños sin requiriendo tamaños de muestra iguales.
- Análisis adimensional : No tienen dimensiones, lo que los hace adecuados para comparar conjuntos de datos con diferentes unidades o escalas.
- Interpretación Visual : Proporciona una representación visual clara de la distribución de datos en comparación con una distribución teórica.
- Sensible a las desviaciones : Detecta fácilmente desviaciones de distribuciones supuestas, lo que ayuda a identificar discrepancias en los datos.
- Herramienta de diagnostico : Ayuda a evaluar supuestos distributivos, identificar valores atípicos y comprender patrones de datos.
Aplicaciones del gráfico cuantil-cuantil
El gráfico Cuantil-Cuantil se utiliza para el siguiente propósito:
- Evaluación de supuestos distributivos : Los gráficos Q-Q se utilizan con frecuencia para inspeccionar visualmente si un conjunto de datos sigue una distribución de probabilidad específica, como la distribución normal. Al comparar los cuantiles de los datos observados con los cuantiles de la distribución supuesta, se pueden detectar desviaciones de la distribución supuesta. Esto es crucial en muchos análisis estadísticos, donde la validez de los supuestos distributivos afecta la precisión de las inferencias estadísticas.
- Detectar valores atípicos : Los valores atípicos son puntos de datos que se desvían significativamente del resto del conjunto de datos. Los gráficos Q-Q pueden ayudar a identificar valores atípicos al revelar puntos de datos que están lejos del patrón esperado de la distribución. Los valores atípicos pueden aparecer como puntos que se desvían de la línea recta esperada en el gráfico.
- Comparación de distribuciones : Los gráficos Q-Q se pueden utilizar para comparar dos conjuntos de datos y ver si provienen de la misma distribución. Esto se logra comparando los cuantiles de un conjunto de datos con los cuantiles de otro conjunto de datos. Si los puntos caen aproximadamente a lo largo de una línea recta, sugiere que los dos conjuntos de datos provienen de la misma distribución.
- Evaluación de la normalidad : Los gráficos Q-Q son particularmente útiles para evaluar la normalidad de un conjunto de datos. Si los puntos de datos en el gráfico siguen una línea recta, indica que el conjunto de datos tiene una distribución aproximadamente normal. Las desviaciones de la línea sugieren desviaciones de la normalidad, lo que puede requerir más investigación o técnicas estadísticas no paramétricas.
- Modelo de validación : En campos como la econometría y el aprendizaje automático, los gráficos Q-Q se utilizan para validar modelos predictivos. Al comparar los cuantiles de las respuestas observadas con los cuantiles predichos por un modelo, se puede evaluar qué tan bien se ajusta el modelo a los datos. Las desviaciones del patrón esperado pueden indicar áreas donde el modelo necesita mejorar.
- Control de calidad : Los gráficos Q-Q se emplean en procesos de control de calidad para monitorear la distribución de los valores medidos u observados a lo largo del tiempo o entre diferentes lotes. Las desviaciones de los patrones esperados en la trama pueden indicar cambios en los procesos subyacentes, lo que impulsará una mayor investigación.
Tipos de gráficos Q-Q
Existen varios tipos de gráficos Q-Q comúnmente utilizados en estadística y análisis de datos, cada uno de ellos adecuado para diferentes escenarios o propósitos:
- Distribución normal : Una distribución simétrica donde el gráfico Q-Q mostraría puntos aproximadamente a lo largo de una línea diagonal si los datos siguen una distribución normal.
- Distribución sesgada a la derecha : Una distribución en la que el gráfico Q-Q mostraría un patrón en el que los cuantiles observados se desvían de la línea recta hacia el extremo superior, lo que indica una cola más larga en el lado derecho.
- Distribución sesgada a la izquierda : Una distribución en la que el gráfico Q-Q mostraría un patrón en el que los cuantiles observados se desvían de la línea recta hacia el extremo inferior, lo que indica una cola más larga en el lado izquierdo.
- Distribución poco dispersa : Una distribución en la que el gráfico Q-Q mostraría los cuantiles observados agrupados más estrechamente alrededor de la línea diagonal en comparación con los cuantiles teóricos, lo que sugiere una varianza más baja.
- Distribución excesivamente dispersa : Una distribución en la que el gráfico Q-Q mostraría los cuantiles observados más dispersos o desviándose de la línea diagonal, lo que indica una mayor varianza o dispersión en comparación con la distribución teórica.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Producción:
Gráfico Q-Q para diferentes distribuciones
preity zinta
