Polígono en matemáticas Es una forma bidimensional formada por líneas rectas que forman una cadena poligonal cerrada. La palabra polígono proviene de las palabras poli y gon, que significan muchos y lados.
Los polígonos pueden ser simples o autointerseccionados. Un polígono simple no se corta a sí mismo, excepto en los extremos compartidos de segmentos consecutivos. Una cadena poligonal que se cruza sobre sí misma crea un polígono que se cruza a sí mismo. Los polígonos también se pueden clasificar en cóncavos o convexos.
En este artículo, mencionamos en detalle los polígonos y sus tipos, fórmulas y ejemplos.
| Datos importantes sobre los polígonos | |
|---|---|
| Suma de ángulos interiores de polígono | (n–2) × 180° |
| Número de diagonales en un polígono | norte(norte–3)/2 |
| Ángulo interior de un polígono regular | {(n–2) × 180°}/n |
| Ángulo exterior de un polígono regular | 360°/n |
Tabla de contenidos
- ¿Qué son los polígonos?
- Gráfico de polígonos basado en el número de lados
- Propiedades de los polígonos
- Formas poligonales
- Tipos de polígonos
- Fórmulas de polígonos
- Ángulos en polígonos
- Preguntas frecuentes
¿Qué son los polígonos?
El término 'polígono' proviene de la palabra griega polugonos, donde 'poli' significa 'muchos' y 'gon' denota 'ángulo'. Generalmente, un polígono es una figura cerrada formada por líneas rectas, con sus ángulos interiores creados por estas. líneas. Para constituir una forma cerrada, es necesario un mínimo de tres segmentos de línea. Se le conoce comúnmente como Triángulo o 3-gón. El término general para un polígono de n lados es n-gón.
Definición de polígono
polígonos Son figuras planas bidimensionales compuestas de lados rectos que forman una forma completamente cerrada. En geometría, el polígono es una figura plana formada por segmentos de línea conectados para formar una cadena poligonal cerrada. Consisten en lados rectos, no curvos, y pueden tener un número variable de lados. Algunos polígonos de diferentes tipos son: abiertos, de solo límite, cerrados y que se intersectan a sí mismos.
En geometría, un polígono se define como una forma bidimensional cerrada que se encuentra plana en un plano y está rodeada por lados rectos.
Un polígono carece de lados curvos y sus aristas son los segmentos rectos que definen su límite. Los puntos de encuentro de estas aristas se denominan vértices o esquinas.
Ejemplos de polígonos
En términos matemáticos, los triángulos, hexágonos, pentágonos y cuadriláteros son ejemplos de polígonos. Ejemplos de Polygon en la vida real son la pantalla de forma rectangular de su computadora portátil, televisión o teléfono móvil; campo de fútbol rectangular o parque infantil, el Triángulo de las Bermudas y las Pirámides de Egipto de forma triangular.

Partes de un polígono
Un Polígono consta de tres componentes fundamentales:
- Lados del polígono: Los lados de un polígono son el límite de los polígonos que definen la región cerrada.
- Vértices: El punto en el que se encuentran dos lados se conoce como vértice.
- Anglos: El polígono contiene ángulos tanto interiores como exteriores. Un ángulo interior se forma dentro de la región encerrada del polígono por la intersección de sus lados.
Gráfico de polígonos basado en el número de lados
Nomenclatura de polígono definida en función del número de lados que posee. Se designa como n-gonos, donde 'n' significa el número de lados. Los polígonos generalmente se identifican por la cantidad de sus aristas. Por ejemplo, un polígono con cinco lados se denomina 5-gonos, mientras que uno con diez lados se denomina 10-gonos.
| Gráfico de polígonos | ||||
|---|---|---|---|---|
| Nombres de formas poligonales | Número de lados | Número de vértices | Número de diagonales | Medida de ángulo interior para forma regular |
| Triángulo | polígonos de 3 lados | 3 | 0 | 60° |
| Cuadrilátero | polígonos de 4 lados | 4 | 2 | 90° |
| Pentágono | Polígonos de 5 lados | 5 | 5 cadena del convertidor hasta la fecha | 108° |
| Hexágono | Polígonos de 6 lados | 6 | 9 | 120° |
| Heptágono | Polígonos de 7 lados. | 7 | 14 | 128.571° |
| Octágono | Polígonos de 8 lados | 8 | 20 | 135° |
| Nonágono | polígonos de 9 lados | 9 | 27 | 140° |
| Decágono | Polígonos de 10 lados | 10 | 35 | 144° |
| Endecágono | Polígonos de 11 lados | 11 | 44 | 147.273° |
| Dodecágono | Polígonos de 12 lados | 12 | 54 | 150° |
Propiedades de los polígonos
Las propiedades de los polígonos los identifican fácilmente. Las siguientes propiedades contribuyen a conocer los Polígonos fácilmente:
- Un polígono es una forma cerrada, sin extremos abiertos. El origen y el punto final deben ser los mismos.
- Asume una forma plana, que consta de segmentos de línea o líneas rectas que en conjunto dan forma a la figura.
- Como entidad bidimensional, un polígono existe sólo en las dimensiones de largo y ancho, sin profundidad ni altura.
- Posee tres o más lados para formar un polígono.
- Los ángulos en el polígono pueden variar. Muestra una configuración distinta.
- La longitud de los lados de un polígono puede variar; puede o no ser igual en todo el polígono.
Formas poligonales
Un polígono es una forma plana bidimensional caracterizada por lados rectos conectados para formar una figura cerrada. Ejemplos de formas poligonales incluyen:
- Triángulo
- Cuadrilátero
- Pentágono
- Hexágono
- Heptágono
- Octágono
- Nonágono
- Decágono
Triángulo
- Tiene 3 lados y 3 vértices.
- No tiene diagonales.
- La suma del interior es 180°.
Cuadrilátero
- Tiene 4 lados y 4 vértices.
- Tiene 2 diagonales.
- La suma de los ángulos interiores es 360°.
Pentágono
- Tiene 5 lados y 5 vértices.
- Tiene 5 diagonales.
- La suma de los ángulos interiores es 540°.
Hexágono
- Tiene 6 lados y 6 vértices.
- Tiene 9 diagonales.
- La suma de los ángulos interiores es 720°.
Heptágono
- Tiene 7 lados y 7 vértices.
- Tiene 14 diagonales.
- La suma de los ángulos interiores es 900°.
Octágono
- Tiene 8 lados y 8 vértices.
- Tiene 20 diagonales.
- La suma de los ángulos interiores es 1080°.
Nonágono
- Tiene 9 lados y 9 vértices.
- Tiene 27 diagonales.
- La suma de los ángulos interiores es 1260°.
Decágono
- Tiene 10 lados y 10 vértices.
- Tiene 35 diagonales.
- La suma de los ángulos interiores es 1440°.
Tipos de polígonos
Dependiendo de los lados y ángulos, los polígonos se pueden clasificar en diferentes tipos según diferentes bases, como por ejemplo:
- Sobre la base de los lados
- Sobre la base de los ángulos
- Sobre la base de los límites
Polígonos sobre la base de los lados
Los polígonos se pueden clasificar según las características de sus lados en dos tipos principales:
- Polígono regular
- polígono irregular
Polígono regular
Un polígono regular se distingue por tener todos los lados de igual longitud y todos los ángulos interiores de iguales medidas. Puede ser tanto equilátero como equiangular. Ejemplos de polígonos regulares incluyen el triángulo, el cuadrilátero, el pentágono y el hexágono.

Polígono regular
polígono irregular
Un polígono irregular tiene lados de longitud desigual y ángulos de medidas variables. Cualquier polígono que no se ajuste a los criterios de un polígono regular se clasifica como irregular. Ejemplos comunes de polígonos irregulares son el triángulo escaleno, cuadriláteros como el rectángulo, el trapecio o la cometa, así como estructuras irregulares de pentágono y hexágono.
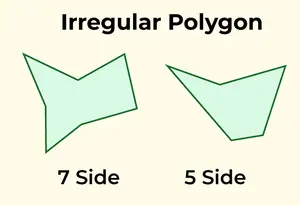
polígono irregular
Polígonos basados en ángulos
Los polígonos se pueden clasificar según la naturaleza de sus ángulos en dos categorías principales:
- Polígono convexo
- Polígono cóncavo
Polígono convexo
Un polígono convexo no tiene ningún ángulo interior que mida más de 180°. Los polígonos convexos pueden tener tres o más lados. En los polígonos convexos, todas las diagonales se encuentran dentro de la figura cerrada. Ejemplos comunes de polígonos convexos son los triángulos, todos los cuadriláteros convexos, así como los pentágonos y hexágonos regulares.
Polígono cóncavo
Un polígono cóncavo tiene al menos un ángulo interior que es un ángulo reflejo y apunta hacia adentro. Los polígonos cóncavos tienen un mínimo de cuatro lados. Este tipo de polígono presenta al menos un ángulo interior que mide más de 180°. En los polígonos cóncavos, algunas diagonales se extienden fuera de la figura encerrada. Ejemplos de polígonos cóncavos incluyen un dardo o una punta de flecha en los cuadriláteros, así como ciertos pentágonos y hexágonos irregulares.
Diferencia entre polígonos cóncavos y convexos
Veamos la diferencia entre polígono convexo y cóncavo en la siguiente tabla:

| Polígono convexo | Polígono cóncavo |
|---|---|
| Todo el perímetro de una forma convexa se extiende hacia afuera sin hendiduras hacia adentro. | Una forma cóncava presenta al menos una porción que apunta hacia adentro, lo que indica la presencia de una abolladura. |
| En un polígono convexo, todos los ángulos internos son inferiores a 180°. | En un polígono cóncavo existe al menos un ángulo interior superior a 180°. |
| Cualquier línea que conecte dos vértices de una forma convexa se encuentra completamente dentro de los límites de la forma. | La línea que conecta dos vértices cualesquiera de una forma cóncava puede o no cruzar el interior de la forma. |
Polígonos basados en límites
Los polígonos se pueden clasificar según la naturaleza de sus límites en dos tipos principales:
- Polígono simple
- Polígono complejo
Polígono simple
Un polígono simple se caracteriza por un límite singular que no se cruza. En otras palabras, no se cruza a sí mismo y consta de un límite.
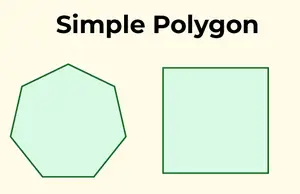
Polígonos simples
Polígono complejo
Por otro lado, un Polígono Complejo se define por su intersección. Consta de más de un límite dentro de su estructura. En los polígonos complejos, el límite se cruza, creando múltiples regiones distintas dentro del polígono.

Polígono complejo
Leer más sobre Tipos de polígonos.
Fórmulas de polígonos
Existen varias fórmulas relacionadas con los polígonos en geometría. Algunos de los más utilizados incluyen:
- Fórmula de área
- Fórmula del perímetro
- Número de diagonales
Todas las fórmulas relacionadas con diferentes polígonos se analizan a continuación:
Área de polígonos
Área de un polígono representa el espacio total que ocupa en un plano bidimensional, está determinado por fórmulas específicas basadas en el número de lados y la clasificación del polígono. Las fórmulas de área son las siguientes:
| Área del polígono | Fórmula |
|---|---|
| Área del Triángulo | 1/2 × Base × Alto |
| Área del paralelogramo | Base × Altura |
| Área de un rectángulo | Largo × Ancho |
| Área de la plaza | (Lado)2 |
| 1/2 × diagonal1×diagonal2 | |
| Área del Trapecio | 1/2 × Altura × Suma de lados paralelos |
| (5/2) × longitud del lado × Apotema | |
| Área del hexágono | {(3√3)/2}lado2 |
| Área del heptágono | 3.643 × Lado2 |
Perímetro de polígonos
El perímetro de una forma bidimensional representa la longitud total de su límite exterior. Para polígonos, el perímetro se calcula de la siguiente manera:
| Perímetro del polígono | Fórmula |
|---|---|
| Perímetro del triángulo | Suma de tres lados |
| Perímetro del paralelogramo | 2 (suma de lados adyacentes) |
| Perímetro del rectángulo | 2(largo + ancho) |
| Perímetro de la plaza | 4 × lateral |
| Perímetro del rombo | 4 × lateral |
| Perímetro del trapecio | Suma de lados paralelos + Suma de lados no paralelos |
| Perímetro del Pentágono | 5 × lateral |
| Perímetro del hexágono | 6 × lado |
| Perímetro del heptágono | 7 × lado |
Fórmula de la diagonal del polígono
Una diagonal de un polígono es un segmento de recta formado al conectar dos vértices que no son adyacentes.
Número de diagonales en un polígono = n(n−3)/2,
Donde 'n' representa el número de lados que posee el polígono.
Leer más sobre Fórmula de la diagonal del polígono .
Ángulos en polígonos
En geometría, los ángulos en polígonos se refieren a los ángulos formados por los lados de un polígono, tanto en el interior como en el exterior del polígono. Por lo tanto, puede haber ambos ángulos en un polígono, es decir,
- Interior Angles
- Exterior Angles
Analicemos en detalle la fórmula de estos ángulos de la siguiente manera:
Fórmula del ángulo interior de los polígonos
Los ángulos interiores de un polígono son los que se forman entre sus lados adyacentes y son iguales en el caso de un polígono regular. El recuento de ángulos interiores corresponde al número de lados del polígono.
La suma de los ángulos interiores 'S' en un polígono con 'n' lados se calcula como
S = (norte – 2) × 180°
Donde 'n' representa el número de lados.
Fórmula del ángulo exterior de los polígonos
Cada ángulo exterior de un polígono regular se forma extendiendo uno de sus lados (ya sea en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj) y midiendo el ángulo entre esta extensión y el lado adyacente. En un polígono regular todos los ángulos exteriores son iguales.
La suma total de los ángulos exteriores de cualquier polígono se fija en 360°.
Por lo tanto,
Cada ángulo exterior está dado por 360°/n
Donde 'n' es el número de lados.
La suma de los ángulos interiores y exteriores correspondientes en cualquier vértice de un polígono es siempre 180 grados, lo que expresa una relación suplementaria:
Interior angle + Exterior angle = 180°
Exterior angle = 180° – Interior angle
Conclusión
- Polígono es una figura cerrada delimitada por tres o más segmentos de recta.
- Suma de ángulos interiores: La suma de todos los ángulos interiores en un polígono de n lados viene dada por la fórmula (n–2)×180°.
- Número de diagonales: Para un polígono con n lados, el número de diagonales se calcula mediante la fórmula n(n–3)/2.
- Triángulos formados por diagonales: El número de triángulos formados al unir diagonales desde una sola esquina de un polígono es n–2.
- Ángulo interior de un polígono regular: La medida de cada ángulo interior en un polígono regular de n lados es {(n–2)×180°}/n.
- Ángulo exterior de un polígono regular: La medida de cada ángulo exterior en un polígono regular de n lados es 360°/n.
Además, lea
- Cuadrado
- Paralelogramo
- Rectángulo
Ejemplos resueltos sobre polígonos en matemáticas
Ejemplo 1: Considere un cuadrilátero de cuatro lados. Encuentra la suma de todos sus ángulos interiores del cuadrilátero.
Solución:
Fórmula para la suma de ángulos interiores en un polígono regular de n lados = (n − 2) × 180°
La suma de todos los ángulos interiores del cuadrilátero = (4 – 2) × 180°
La suma de todos los ángulos interiores del cuadrilátero = 2 × 180°
La suma de todos los ángulos interiores del cuadrilátero = 360°
Por tanto, la suma de todos los ángulos interiores del cuadrilátero es 360°.
Ejemplo 2: Considere un polígono regular con una relación de ángulos exterior e interior dada de 7:3. Determina el tipo de polígono.
Solución:
La relación entre el ángulo exterior e interior es 7:3.
Suponga que los ángulos exterior e interior de un polígono son 7x y 3x.
La suma de los ángulos exterior e interior de cualquier polígono es 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Exterior angle = 18°
Número de lados = 360°/ángulo exterior
= 360°/18°
= 20
Por tanto, el polígono dado es un icoságono, ya que tiene 20 lados.
Ejemplo 3: Cada Ángulo Exterior de un Polígono mide 90 grados, ¿determina el tipo de Polígono?
Solución:
Según la fórmula, cada ángulo exterior = 360°/n
Aquí n=número de lados.
90°= 360°/n
norte = 360°/90°= 4
Por tanto, el polígono en cuestión es un cuadrilátero, ya que posee cuatro lados.
Ejemplo 4: Los lados son 10m, 10m, 8m, 8m, 5m, 5m, 9m, 9m. ¿Cuántos metros de cuerda se necesitarán para el perímetro?
Solución:
tabla de reacción
Para encontrar la longitud de la cuerda necesaria para el perímetro, debemos sumar las longitudes de todos los lados:
Perímetro = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Perímetro = 64 m.
Por tanto, se necesitarán un total de 64 metros de cuerda para el Perímetro.
Preguntas de práctica sobre polígonos en geometría
A continuación se presentan algunas preguntas de práctica basadas en la fórmula de polígonos:
P1. Dado que un ángulo de un pentágono mide 140°, determina el tamaño del ángulo más grande si los ángulos restantes están en la proporción 1:2:3:4.
P2. Si la suma de los ángulos interiores de un polígono es 160°, encuentra el número de lados del polígono.
P3. El número de lados de dos polígonos regulares está en proporción 2:3 y la proporción de sus ángulos interiores es 4:5. Encuentra los respectivos números de lados de estos polígonos.
P4. Determina la suma total de los ángulos de un heptágono.
P5. Calcula la suma de los ángulos exteriores de un pentágono.
P6. ¿Cuántos lados tiene un hexágono?
- 4
- 6
- 8
- 10
P7. ¿Cuál de los siguientes no es un polígono regular?
- Triángulo
- Cuadrado
- Pentágono
- Paralelogramo
Preguntas frecuentes sobre polígonos en matemáticas
¿Qué es un polígono en matemáticas?
En matemáticas, un polígono se refiere a una figura bidimensional cerrada formada por la conexión de tres o más líneas rectas. El término polígono se deriva del idioma griego, donde poli- significa muchos y gon representa ángulo.
¿Cuál es el polígono más pequeño?
El polígono más pequeño formado es un triángulo de tres lados.
¿Qué es 20 gon?
Un 20 gon es un polígono de veinte lados en geometría.
¿Cuál es la suma total de los ángulos externos de un polígono?
La suma de los ángulos exteriores de un polígono es 360°.
¿Se puede clasificar un círculo como polígono?
Un polígono es una forma cerrada formada por segmentos de línea recta. El círculo es una figura cerrada, pero está formada por una curva. Entonces un círculo no es un polígono.
¿Cuál es la suma de los ángulos interiores de un polígono?
La suma del ángulo interior de un polígono viene dada por (n–2)×180° donde n es el número de lados del polígono.
