Requisito previo: Introducción a los consejos

Considere el siguiente programa:

C

>

>

En el programa anterior, tenemos un puntero. ptr que apunta al 0^thelemento de la matriz. De manera similar, también podemos declarar un puntero que pueda apuntar a una matriz completa en lugar de solo a un elemento de la matriz. Este puntero es útil cuando se habla de matrices multidimensionales.

Sintaxis:

data_type  (* var_name ) [size_of_array];>

Aquí:

tipo_datos es el tipo de datos que contiene la matriz. var_name es el nombre de la variable de puntero. size_of_array es el tamaño de la matriz a la que apuntará el puntero.

Ejemplo

int (*ptr)[10];>

Aquí ptr es un puntero que puede apuntar a una matriz de 10 números enteros. Dado que los subíndices tienen mayor prioridad que la indirección, es necesario encerrar el operador de indirección y el nombre del puntero entre paréntesis. Aquí el tipo de ptr es 'puntero a una matriz de 10 números enteros'.

Nota: El puntero que apunta al 0^thEl elemento de la matriz y el puntero que apunta a toda la matriz son totalmente diferentes. El siguiente programa muestra esto:

C

>

>

p = 0x7fff6463e890, ptr = 0x7fff6463e890 p = 0x7fff6463e894, ptr = 0x7fff6463e8a4>

Aquí, pag es puntero a 0^thelemento de la matriz llegar , mientras ptr es un puntero que apunta a toda la matriz llegar .

• El tipo básico de pag es int mientras que el tipo base de ptr es 'una matriz de 5 números enteros'.
• Sabemos que la aritmética del puntero se realiza en relación con el tamaño de la base, por lo que si escribimos ptr++, entonces el puntero ptr se adelantará 20 bytes.

La siguiente figura muestra el puntero p y ptr. La flecha más oscura indica un puntero a una matriz.

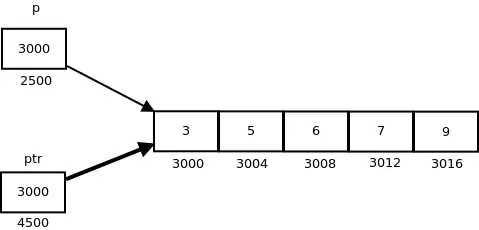
Al eliminar la referencia a una expresión de puntero, obtenemos un valor al que apunta esa expresión de puntero. El puntero a una matriz apunta a una matriz, por lo que al eliminar la referencia a ella, deberíamos obtener la matriz, y el nombre de la matriz indica la dirección base. Entonces, cada vez que se desreferencia un puntero a una matriz, obtenemos la dirección base de la matriz a la que apunta.

C

>

>

p = 0x7fff55adbff0, ptr = 0x7fff55adbff0 *p = 3, *ptr = 0x7fff55adbff0 sizeof(p) = 8, sizeof(*p) = 4 sizeof(ptr) = 8, sizeof(*ptr) = 20>

Puntero a matrices multidimensionales

1. Punteros y matrices bidimensionales

En una matriz bidimensional, podemos acceder a cada elemento mediante el uso de dos subíndices, donde el primer subíndice representa el número de fila y el segundo subíndice representa el número de columna. También se puede acceder a los elementos de la matriz 2-D con la ayuda de la notación de puntero. Supongamos que arr es una matriz 2D, podemos acceder a cualquier elemento arr[i][j] de la matriz usando la expresión de puntero *(*(arr + i) + j) . Ahora veremos cómo se puede derivar esta expresión.
Tomemos una matriz bidimensional llegar[3][4] :

int arr[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} };>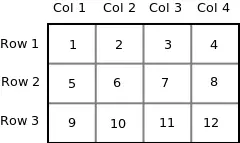

Dado que la memoria en una computadora está organizada linealmente, no es posible almacenar la matriz 2D en filas y columnas. El concepto de filas y columnas es sólo teórico; en realidad, una matriz 2-D se almacena en orden de fila principal, es decir, las filas se colocan una al lado de la otra. La siguiente figura muestra cómo se almacenará en la memoria la matriz 2-D anterior.

Cada fila puede considerarse como una matriz unidimensional, por lo que una matriz bidimensional puede considerarse como una colección de matrices unidimensionales que se colocan una tras otra. En otras palabras, podemos decir que son matrices bidimensionales que se colocan una tras otra. Así que aquí llegar es una matriz de 3 elementos donde cada elemento es una matriz unidimensional de 4 números enteros.
Sabemos que el nombre de una matriz es un puntero constante que apunta a 0^thmatriz 1-D y contiene la dirección 5000. Desde llegar es un 'puntero a una matriz de 4 enteros', según la aritmética de punteros, la expresión arr + 1 representará la dirección 5016 y la expresión arr + 2 representará la dirección 5032.
Entonces podemos decir que llegar apunta al 0^thmatriz 1-D, llegar + 1 apunta al 1^callematriz 1-D y llegar + 2 apunta a los 2^{Dakota del Norte}Matriz 1-D.

En general podemos escribir:

 arr + i Points to ith element of arr ->Apunta a la matriz 1-D>

• Dado que arr + i apunta a i^thelemento de llegar , al desreferenciar obtendré^thelemento de llegar que por supuesto es una matriz 1-D. Así la expresión *(arr + i) nos da la dirección base de i^thMatriz 1-D.
• Ya sabemos, la expresión del puntero. *(arr + i) es equivalente a la expresión del subíndice llegar[yo] . Entonces *(arr + i) que es lo mismo que llegar[yo] nos da la dirección base de i^thMatriz 1-D.
• Para acceder a un elemento individual de nuestra matriz 2-D, deberíamos poder acceder a cualquier j^thelemento de yo^thMatriz 1-D.
• Dado que el tipo base de *(arr + i) es En t y contiene la dirección de 0^thelemento de yo^thmatriz 1-D, podemos obtener las direcciones de los elementos posteriores en la i^thMatriz 1-D agregando valores enteros a *(arr + i) .
• Por ejemplo *(arreglo + i) + 1 representará la dirección de 1^calleelemento de 1^calleelemento de yo^thmatriz 1-D y *(arr+i)+2 representará la dirección de 2^{Dakota del Norte}elemento de yo^thMatriz 1-D.
• De manera similar *(arr + i) + j representará la dirección de j^thelemento de yo^thMatriz 1-D. Al desreferenciar esta expresión podemos obtener la j^thelemento de la i^thMatriz 1-D.

Punteros y matrices tridimensionales

int arr[2][3][2] = { {{5, 10}, {6, 11}, {7, 12}}, {{20, 30}, {21, 31}, {22, 32}} };>

En una matriz tridimensional podemos acceder a cada elemento utilizando tres subíndices. Tomemos una matriz tridimensional. Podemos considerar que una matriz tridimensional es una matriz de una matriz bidimensional, es decir, cada elemento de una matriz tridimensional se considera una matriz bidimensional. La matriz tridimensional llegar Puede considerarse como una matriz que consta de dos elementos, donde cada elemento es una matriz bidimensional. El nombre de la matriz llegar es un puntero al 0^thMatriz 2D.

Así, la expresión del puntero *(*(*(arr + i ) + j ) + k) es equivalente a la expresión de subíndice arr[i][j][k].
Sabemos que la expresión *(arr + i) es equivalente a arr[i] y la expresión *(*(arr + i) + j) es equivalente a arr[i][j]. Entonces podemos decir que arr[i] representa la dirección base de i^thMatriz 2-D y arr[i][j] representa la dirección base de j^thMatriz 1-D.

Ejemplo

booleano a cadena java

El siguiente ejemplo demuestra el programa para imprimir elementos de una matriz 3D utilizando punteros.

C

>

>

5 10 6 11 7 12 20 30 21 31 22 32>

La siguiente figura muestra cómo se almacena en la memoria la matriz 3-D utilizada en el programa anterior.

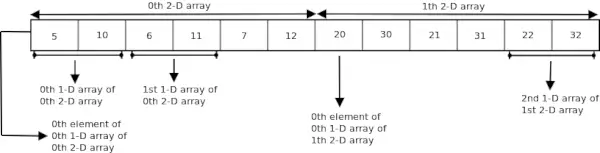
Puntero de suscripción a una matriz

Suponer llegar es una matriz 2-D con 3 filas y 4 columnas y ptr es un puntero a una matriz de 4 números enteros, y ptr contiene la dirección base de la matriz llegar .

int arr[3][4] = {{10, 11, 12, 13}, {20, 21, 22, 23}, {30, 31, 32, 33}}; int (*ptr)[4]; ptr = arr;>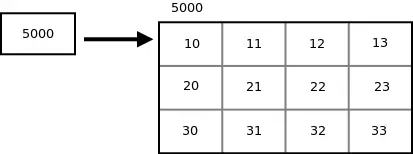

Desde ptr es un puntero a la matriz 2D de la primera fila, es decir, una matriz de 4 números enteros, ptr + yo me señalará^thfila. Sobre la desreferenciación ptr + yo , obtenemos la dirección base de i^thfila. Para acceder a la dirección de j^thelemento de yo^thfila podemos agregar j a la expresión del puntero *(ptr + i) . Entonces la expresión del puntero *(ptr + i) + j da la dirección de j^thelemento de yo^thfila y la expresión del puntero *(*(ptr + i)+j) da el valor de j^thelemento de yo^thfila.
Sabemos que la expresión de puntero *(*(ptr + i) + j) es equivalente a la expresión de subíndice ptr[i][j]. Entonces, si tenemos una variable de puntero que contiene la dirección base de una matriz 2-D, entonces podemos acceder a los elementos de la matriz subscribiendo dos veces esa variable de puntero.

Ejemplo

C

>

>

0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 10 22 33 10 22 33>