En informática existen algunos problemas cuyas soluciones aún no se encuentran, los problemas se dividen en clases conocidas como Clases de complejidad . En teoría de la complejidad, una clase de complejidad es un conjunto de problemas con complejidad relacionada. Estas clases ayudan a los científicos a agrupar problemas según el tiempo y el espacio que requieren para resolverlos y verificar las soluciones. Es la rama de la teoría de la computación que se ocupa de los recursos necesarios para resolver un problema.
cadena reemplaza todo java
Los recursos comunes son el tiempo y el espacio, es decir, cuánto tiempo tarda el algoritmo en resolver un problema y el uso de memoria correspondiente.
- La complejidad temporal de un algoritmo se usa para describir la cantidad de pasos necesarios para resolver un problema, pero también se puede usar para describir cuánto tiempo lleva verificar la respuesta.
- La complejidad espacial de un algoritmo describe cuánta memoria se requiere para que funcione el algoritmo.
Las clases de complejidad son útiles para organizar tipos similares de problemas.
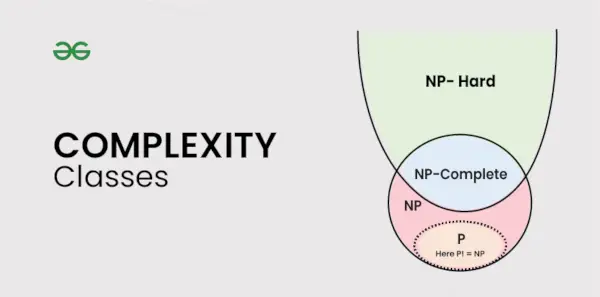
Tipos de clases de complejidad
Este artículo analiza las siguientes clases de complejidad:
- Clase P
- Clase NP
- Clase CoNP
- NP-duro
- NP-completo
Clase P
La P en la clase P significa Tiempo polinomial. Es el conjunto de problemas de decisión (problemas con respuesta sí o no) que pueden resolverse mediante una máquina determinista en tiempo polinomial.
Características:
- La solución a problema p s es fácil de encontrar.
- PAG Es a menudo una clase de problemas computacionales que son solucionables y manejables. Tratable significa que los problemas pueden resolverse tanto en teoría como en la práctica. Pero los problemas que pueden resolverse en teoría pero no en la práctica se conocen como intratables.
Esta clase contiene muchos problemas:
- Calcular el máximo común divisor.
- Encontrar una coincidencia máxima.
- Combinar ordenar
Clase NP
El NP en la clase NP significa Tiempo polinómico no determinista . Es el conjunto de problemas de decisión que pueden resolverse mediante una máquina no determinista en tiempo polinomial.
Características:
- Las soluciones de la clase NP son difíciles de encontrar ya que se resuelven mediante una máquina no determinista, pero las soluciones son fáciles de verificar.
- Los problemas de NP pueden verificarse mediante una máquina de Turing en tiempo polinomial.
Ejemplo:
Consideremos un ejemplo para comprender mejor el clase NP . Supongamos que hay una empresa que tiene un total de 1000 empleados que tienen empleado único identificaciones . Supongamos que hay 200 habitaciones disponibles para ellos. Una selección de 200 Los empleados deben estar emparejados, pero el director ejecutivo de la empresa tiene los datos de algunos empleados que no pueden trabajar en la misma habitación por motivos personales.
Este es un ejemplo de un P.EJ problema. Dado que es fácil comprobar si la elección dada de 200 empleados propuestos por un compañero de trabajo es satisfactorio o no, es decir, ningún par tomado de la lista de compañeros de trabajo aparece en la lista proporcionada por el CEO. Pero generar una lista así desde cero parece ser tan difícil que resulta completamente impracticable.
ventana.abrir javascript
Indica que si alguien puede brindarnos la solución al problema, podremos encontrar el par correcto e incorrecto en tiempo polinomial. Así para el P.EJ problema de clase, la respuesta es posible, la cual se puede calcular en tiempo polinomial.
Esta clase contiene muchos problemas que a uno le gustaría poder resolver de manera efectiva:
- Problema booleano de satisfacción (SAT).
- Problema del camino hamiltoniano.
- Coloración de gráficos.
Clase Co-NP
Co-NP significa el complemento de la Clase NP. Significa que si la respuesta a un problema en Co-NP es No, entonces hay una prueba que se puede verificar en tiempo polinomial.
Características:
- Si un problema X está en NP, entonces su complemento X’ también está en CoNP.
- Para un problema de NP y CoNP, no es necesario verificar todas las respuestas a la vez en tiempo polinómico, es necesario verificar solo una respuesta particular sí o no en tiempo polinómico para que un problema sea en NP o CoNP.
Algunos problemas de ejemplo para CoNP son:
- Para comprobar el número primo.
- Factorización de números enteros.
NP-clase dura
Un problema NP-difícil es al menos tan difícil como el problema más difícil en NP y es una clase de problemas tal que cada problema en NP se reduce a NP-difícil.
Características:
- Todos los problemas NP-difíciles no están en NP.
- Se necesita mucho tiempo para comprobarlos. Esto significa que si se proporciona una solución para un problema NP-difícil, se necesita mucho tiempo para comprobar si es correcta o no.
- Un problema A es NP-difícil si, para cada problema L en NP, existe una reducción de tiempo polinomial de L a A.
Algunos de los ejemplos de problemas en Np-hard son:
- Problema de detención.
- Fórmulas booleanas calificadas.
- Sin ciclo hamiltoniano.
Clase NP-completa
Un problema es NP-completo si es a la vez NP y NP-difícil. Los problemas NP completos son los problemas difíciles en NP.
¿Qué tan grande es este monitor?
Características:
- Los problemas NP completos son especiales ya que cualquier problema de la clase NP se puede transformar o reducir a problemas NP completos en tiempo polinomial.
- Si se pudiera resolver un problema NP-completo en tiempo polinomial, entonces también se podría resolver cualquier problema NP en tiempo polinomial.
Algunos problemas de ejemplo incluyen:
- Ciclo hamiltoniano.
- Satisfacción.
- Cubierta de vértice .
| Clase de complejidad | Característica distintiva |
| PAG | Fácilmente solucionable en tiempo polinomial. |
| P.EJ | Sí, las respuestas se pueden comprobar en tiempo polinómico. |
| Co-NP | No, las respuestas se pueden comprobar en tiempo polinomial. |
| NP-duro | Todos los problemas NP-difíciles no están en NP y lleva mucho tiempo verificarlos. |
| NP-completo | Un problema que es NP y NP-difícil es NP-completo. |
