La fuerza normal se define como la fuerza que ejerce cualquier superficie sobre otro objeto. Cuando un objeto está en reposo, la fuerza neta que se ejerce sobre él es igual a cero. No se puede aplicar una fuerza normal sobre dos superficies que no están conectadas entre sí. Puede interpretarse como una componente de la fuerza vertical a cualquier superficie de contacto. Determina cuánta fuerza entrega el cuerpo al suelo. La fuerza normal es igual al peso del objeto sólo si la tasa de cambio de velocidad del objeto es negativa, lo que significa que está desacelerando.
Fórmula
El valor de la fuerza normal depende de dónde se coloca el objeto con respecto al otro objeto. Cuando un objeto va a caer, la posición en la que cae al suelo determina el valor de la fuerza normal. La fuerza normal se denota con el símbolo F.norte. Su unidad de medida es Newtons (N) y la fórmula dimensional viene dada por [M1l1t-2].
Si un cuerpo reposa sobre una fuerza plana, la fuerza normal es igual al valor del peso gravitacional, es decir, mg.
F norte = mg
dónde,
Fnortees la fuerza normal,
m es la masa del objeto en reposo,
g es la aceleración debida a la gravedad.
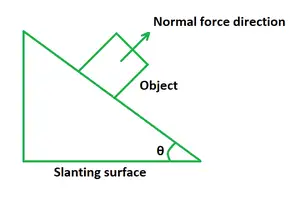
Si un cuerpo se desliza hacia abajo desde una superficie inclinada en algún ángulo, el valor de la fuerza normal es el peso gravitacional agregado por una fuerza adicional de F sen θ. En este caso, la fuerza normal es mayor que el peso del objeto.
F norte = mg + F sen θ
Dónde,
Fnortees la fuerza normal,
m es la masa del objeto deslizante,
g es la aceleración debida a la gravedad,
θ es el ángulo de inclinación.
Si la fuerza actúa sobre un cuerpo en dirección hacia arriba, el valor de la fuerza normal es el peso gravitacional disminuido en una fuerza de F sen θ. En este caso, la fuerza normal neta es menor que el peso del objeto.
F norte = mg – F sen θ
dónde,
fecha actual en javaFnortees la fuerza normal,
m es la masa del objeto deslizante,
g es la aceleración debida a la gravedad,
θ es el ángulo de inclinación.
Si un cuerpo se coloca sobre un plano inclinado, la fuerza normal Fnortees igual al producto del peso gravitacional y el coseno del ángulo de inclinación.
F norte = mg cos θ
dónde,
Fnortees la fuerza normal,
m es la masa del objeto deslizante,
g es la aceleración debida a la gravedad,
θ es el ángulo de inclinación.
Problemas de muestra
Problema 1. Un objeto de 2 kg de masa está apoyado sobre una mesa. Calcule la fuerza normal que se ejerce sobre él.
Solución:
Tenemos,
metro = 2
gramos = 9,8
Usando la fórmula obtenemos,
Fnorte= mg
= 2 (9.8)
= 19,6 norte
Problema 2. Un objeto descansa sobre una mesa con una fuerza de 39,2 N. Calcula la fuerza normal que se ejerce sobre él.
Solución:
Tenemos,
F = 39,2
gramos = 9,8
Usando la fórmula obtenemos,
Fnorte= mg
=> m = F/g
=> metro = 39,2/9,8
=> metro = 4 kilos
Problema 3. Un objeto con una masa de 10 kg se desliza hacia abajo con una fuerza de 200 N desde una superficie inclinada en un ángulo de 30°. Calcule la fuerza normal que se ejerce sobre él.
Solución:
Tenemos,
F = 200
metro = 10
gramos = 9,8
θ = 30°
Usando la fórmula obtenemos,
Fnorte= mg + F sen θ
= 10 (9.8) + 200 sin 30°
= 98 + 200 (1/2)
= 98 + 100
= 198norte
Problema 4. Un objeto de 20 kg de masa se desliza hacia abajo con una fuerza de 400 N desde una superficie inclinada en un ángulo de 30°. Calcule la fuerza normal que se ejerce sobre él.
Solución:
Tenemos,
F = 400
metro = 20
gramos = 9,8
θ = 30°
Usando la fórmula obtenemos,
Fnorte= mg + F sen θ
= 20 (9.8) + 400 sin 30°
¿cuanto pesa kat timpf?= 196 + 400 (1/2)
= 196 + 200
= 396 norte
Problema 5. Un objeto con una masa de 15 kg se coloca sobre una superficie inclinada en un ángulo de 30°. Calcule la fuerza normal que se ejerce sobre él si la fuerza actúa hacia arriba con un valor de 100 N.
Solución:
Tenemos,
F = 100
metro = 15
gramos = 9,8
θ = 30°
Usando la fórmula obtenemos,
Fnorte= mg – F sen θ
= 15 (9.8) – 100 sin 30°
= 147 – 100 (1/2)
= 147 – 50
parafrasear si por rudyard kipling= 97 norte
Problema 6. Un objeto de 5 kg de masa se coloca sobre una superficie inclinada en un ángulo de 60°. Calcule la fuerza normal que se ejerce sobre él en cualquier punto.
Solución:
Tenemos,
metro = 5
gramos = 9,8
θ = 60°
Usando la fórmula obtenemos,
Fnorte= mg cos θ
= 5 (9,8) (cos 60°)
= 49/2
= 24,5 norte
Problema 7. Se coloca un objeto sobre una superficie inclinada en un ángulo de 60°. Calcule su masa si la fuerza normal que se ejerce sobre él es de 400 N.
Solución:
Tenemos,
Fnorte= 400,
θ = 60°
Usando la fórmula obtenemos,
Fnorte= mg cos θ
m = F/(g cos θ)
= 400/ (9,8 × cos 60°)
= 400/4.9
= 81,63 norte
