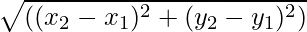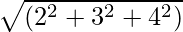logo

TechCodeview

Magnitud de un vector

Las cantidades vectoriales son cantidades que tienen dirección y magnitud. La magnitud de un vector es la longitud del vector. Está dado por el valor numérico del vector y, como representa la longitud del vector, siempre es positivo. Para cualquier vector 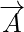overrightarrow{A}su magnitud se representa como overrightarrow{A}.

Aprendamos más sobre la magnitud del vector, su fórmula, ejemplos y otros en este artículo.



Tabla de contenidos

¿Cuál es la magnitud de un vector?

La magnitud de un vector se define como la longitud del vector. Como la magnitud del vector denota la longitud del vector, siempre es positiva. Para cualquier vector A su magnitud se representa como |A|. Supongamos que un vector se define como xi + yj, entonces su magnitud se define como la raíz cuadrada de la suma de los cuadrados de los términos individuales. La magnitud del vector representa la longitud del vector, es decir, el valor o impacto que tiene el vector.

Por ejemplo, si una fuerza de 5i N actúa sobre un objeto, entonces su magnitud es 5 N, lo que significa que la intensidad de la fuerza aplicada es 5 N, y ' i' en 5i representa que se aplica en la dirección x positiva.



Magnitud de una fórmula vectorial

Hay diferentes formas de calcular la magnitud del vector. Con base en los datos dados, usa un tipo diferente de fórmula para encontrar la magnitud de un vector. La magnitud de un vector A se representa mediante el operador de módulo, es decir, |A|

Existen varias fórmulas que se utilizan para contar la magnitud del vector. La siguiente imagen muestra las fórmulas importantes utilizadas para encontrar la magnitud del vector.

Magnitud de una fórmula vectorial

A continuación se muestran las formas de calcular la magnitud.



  • Si se les da un vector Ā = xi+ yĵ + zk̂, entonces la magnitud del vector Ā se puede calcular usando la siguiente fórmula

Magnitud del vector Ā (|A|) = √(x 2 + y 2 +z 2 )

  • Si el vector del punto de partida es digamos (x1, y1) y el punto final de un vector es, por ejemplo, (x2, y2) se dan entonces la magnitud del vector overrightarrow{AB}es dado por,
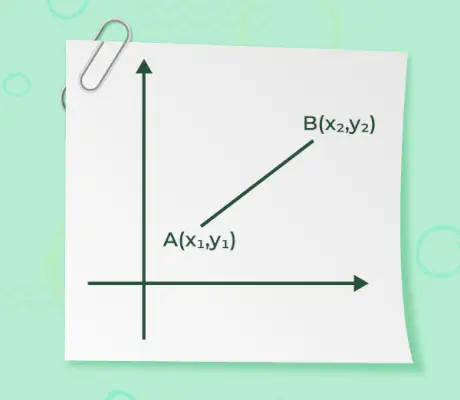
Magnitud del Vector si se dan dos puntos

La magnitud de un vector, cuando se dan los puntos inicial y final de un vector, no es más que la distancia entre los puntos. La fórmula para encontrar la magnitud está dada por

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Si cualquiera de los puntos inicial o final de un vector está en el origen o(0, 0) y otro punto está A(x, y) como se especifica en la siguiente figura,
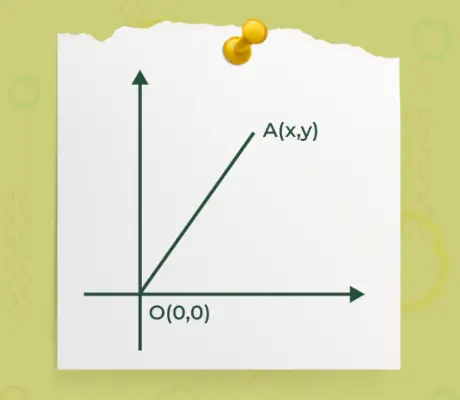
Magnitud del Vector si se da un punto y origen

Entonces la fórmula para encontrar la magnitud de un vector donde uno de los extremos de un vector está en el origen está dada por

|Ā| = √(x 2 +y 2 )

Dirección de un vector

Las cantidades vectoriales son cantidades que tienen magnitudes y direcciones. La dirección de la cantidad vectorial significa en qué dirección se aplica la cantidad vectorial. Se define como el ángulo que forma el vector con la línea horizontal o el eje x. Está representado por el símbolo a .

La siguiente imagen muestra la flecha que se utiliza para mostrar la dirección del vector.

Dirección del vector

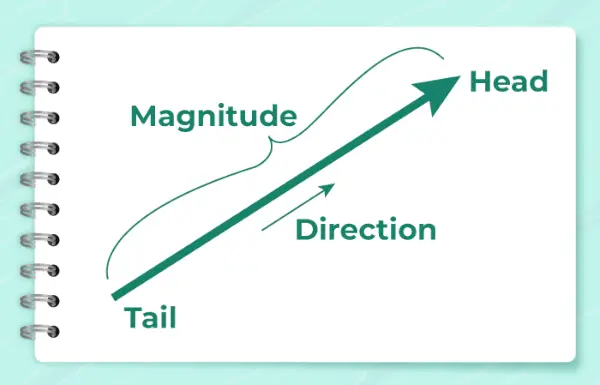
Se calcula mediante la fórmula,

α = tan -1 (y/x)

milivecriclet

Para el vector generado por las coordenadas (x1, y1) y (x2, y2) su dirección viene dada por la fórmula,

α = tan -1 [(y 2 – y 1 )/(X 2 - X 1 )]

¿Cómo encontrar la magnitud de un vector?

La magnitud del vector se calcula utilizando los pasos que se describen a continuación,

cómo salir de un bucle while java

Paso 1: Identifica las componentes x, y y z del vector.

Paso 2 : Encuentra el cuadrado de todos los componentes x, y y z.

Paso 3: Agrega todos los cuadrados que se encuentran en el Paso 2.

Etapa 4: Encuentra la raíz cuadrada de la suma obtenida en el Paso 3.

El valor obtenido después del paso 4 es la magnitud del vector dado.

Ejemplo: Encuentre la magnitud del vector A = 3i + 4j

Solución:

La magnitud del vector A se calcula utilizando los pasos discutidos anteriormente.

Paso 1: Comparando A = 3i + 4j con xi + yj obtenemos x = 3 e y = 4

Paso 2: X2= 32= 9 y y2= 42= 16

Paso 3: X2+ y2= 9 + 16 = 25

Etapa 4: √(25) = 5

Por tanto, la magnitud del vector A = 3i + 4j es 5 unidades.

Conclusión

En conclusión, la magnitud de un vector nos dice qué tan largo es el vector. Este concepto es muy importante en muchos campos como la física, la ingeniería y la informática porque ayuda a medir cosas como la velocidad, la fuerza y ​​la dirección del movimiento. Al comprender la magnitud del vector, podemos analizar y resolver mejor problemas prácticos, lo que la convierte en un conocimiento clave para cualquiera que trabaje con números y medidas en aplicaciones del mundo real.

Leer más,

Ejemplos resueltos sobre magnitud de vector

Ejemplo 1: Encuentre la magnitud del vector Ā = 2i + 3ĵ + 4k.

Solución:

Bucle infinito

Dado,

Ā = 2i + 3ĵ + 4k

Magnitud |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5.38

La magnitud del vector. 2i+3ĵ+4k es 5.38 unidad

Ejemplo 2: Encuentre la magnitud del vector Ā = 3i + 3ĵ – 6k

Solución:

Dado

Ā = 3i + 3ĵ – 6k

Magnitud |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7.35

La magnitud del vector. 3i+ 3ĵ – 6k es 7.35 unidad.

Ejemplo 3: Encuentre la magnitud del vector si el punto inicial de un vector es (3, 4) y el punto final es (6, 2).

Solución:

Dado,

(X1, y1) = (3, 4)
(X2, y2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3.6

Por tanto, la magnitud del vector dado es 3.6 unidad.

Ejemplo 4: Encuentre la magnitud del vector si el punto inicial de un vector es (2, 1, 4) y el punto final es (5, 2, 6).

Solución:

Dado,

(X1, y1, Con1) = (2, 1, 4)

(X2, y2, Con2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

multiplexor dos a uno

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3.74

Por tanto, la magnitud del vector dado es 3.74 unidad.

Ejemplo 5: ¿Cuál es la magnitud del vector que comienza en el origen y termina en (3, 4)?

Solución:

Dado,

El punto inicial del vector es O(0, 0)

Punto final (x, y) = (3, 4)

Magnitud del Vector (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Por tanto, la magnitud del vector dado es 5 unidad.

Ejemplo 6: Encuentre la magnitud del vector en el que uno de los puntos finales está en el origen y el otro punto en (1, 4, 3).

Solución:

Dado,

El punto final del vector es O(0, 0)

Otro punto (x, y, z) = (1, 4, 3)

Magnitud del Vector (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5.09

Por tanto, la magnitud del vector dado es 5.09 unidad.

interfaz gráfica de usuario c++

Preguntas frecuentes sobre la magnitud de un vector

¿Cuál es la magnitud de una fórmula vectorial?

La magnitud de un vector es el valor numérico del vector y define la longitud del vector. Para cualquier vector, A su magnitud se representa como |A|. La magnitud del vector se calcula mediante la fórmula,

Para cualquier vector, A = xi + yj + zk su magnitud viene dada por la fórmula

|A| = √(x 2 + y 2 +z 2 )

Para cualquier vector cuyo punto inicial y final sean respectivamente (x1, y1) y (x2, y2) su magnitud está dada por la fórmula

|A| = √((x 2 - X 1 ) 2 + (y 2 – y 1 ) 2 )

¿Cómo representar la Magnitud de un Vector?

La magnitud del vector. A está representado por el símbolo |A|.

¿Cómo encontrar la magnitud de un vector?

Se utilizan varias fórmulas para calcular la magnitud del vector, algunas de ellas son,

  • |A| = √(x 2 + y 2 +z 2 ) cuando el vector tiene la forma A = xi + yj + zk
  • |A| = √((x) 2 + (y) 2 ) cuando el vector está dado por el punto A (x, y) y el origen O(0, 0).
  • |A| = √((x 2 - X 1 ) 2 + (y 2 – y 1 ) 2 ) cuando el vector está dado por el punto A (x1, y2) y el punto B (x2, y2).

Encuentre un vector de magnitud 5.

Hay varios vectores que pueden tener una magnitud de 5, un ejemplo de los cuales es el vector A representado como,

A = 3i + 4j O A = 4i + 5j