El algoritmo de Luhn, también conocido como módulo 10 o hacia 10 algoritmo, es una fórmula de suma de verificación simple que se utiliza para validar una variedad de números de identificación, como números de tarjetas de crédito, números IMEI y números de seguro social canadiense. La fórmula LUHN fue creada a finales de los años 1960 por un grupo de matemáticos. Poco después, las compañías de tarjetas de crédito lo adoptaron. Como el algoritmo es de dominio público, cualquiera puede utilizarlo. La mayoría de las tarjetas de crédito y muchos números de identificación gubernamentales utilizan el algoritmo como un método simple para distinguir números válidos de números mal escritos o incorrectos. Fue diseñado para proteger contra errores accidentales, no contra ataques maliciosos.
Pasos involucrados en el algoritmo de Luhn
Entendamos el algoritmo con un ejemplo:
Considere el ejemplo de un número de cuenta. 79927398713 .
Paso 1 – Comenzando desde el dígito más a la derecha, duplique el valor de cada segundo dígito,
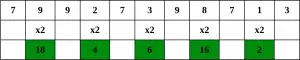
Paso 2 – Si al duplicar un número se obtiene un número de dos dígitos, es decir, mayor que 9 (por ejemplo, 6 × 2 = 12), entonces sume los dígitos del producto (por ejemplo, 12: 1 + 2 = 3, 15: 1 + 5 = 6), para obtener un número de un solo dígito.

Paso 3 – Ahora toma la suma de todos los dígitos.
ubicación df

Etapa 4 – Si el total módulo 10 es igual a 0 (si el total termina en cero), entonces el número es válido según la fórmula de Luhn; de lo contrario no es válido.

Dado que la suma es 70, que es múltiplo de 10, es posible que el número de cuenta sea válido.
La idea es simple; atravesamos desde el final. Por cada segundo dígito, lo duplicamos antes de sumarlo. Sumamos dos dígitos del número obtenido después de duplicar.
Implementación:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; yo--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
al hacer clic en js
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
matriz java para listar
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)> >{> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
>
JavaScript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
borrar caché npm
>Producción
This is a valid card>
El algoritmo de Luhn detecta cualquier error de un solo dígito, así como casi todas las transposiciones de dígitos adyacentes.
