Dadas dos cuerdas, T1 y T2 , la tarea es encontrar la longitud de la subsecuencia común más larga, es decir, la subsecuencia más larga presente en ambas cadenas.
A subsecuencia común más larga (LCS) se define como la subsecuencia más larga que es común en todas las secuencias de entrada dadas.
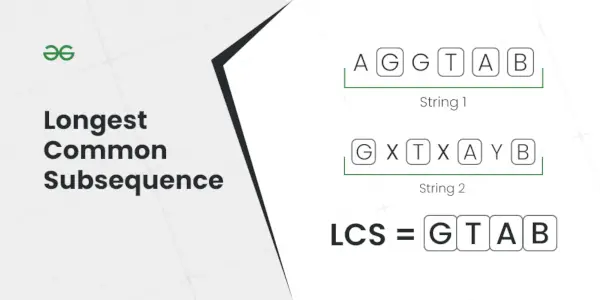
Subsecuencia común más larga
Ejemplos:
Práctica recomendada Subsecuencia común más larga ¡Pruébelo!Aporte: S1 = ABC, S2 = ACD
Producción: 2
Explicación: La subsecuencia más larga que está presente en ambas cadenas es AC.Aporte: S1 = AGGTAB, S2 = GXTXAYB
Producción: 4
Explicación: La subsecuencia común más larga es GTAB.Aporte: S1 = ABC, S2 = CBA
Producción: 1
Explicación: Hay tres subsecuencias comunes de longitud 1, A, B y C y ninguna subsecuencia común de longitud superior a 1.recorrido en ordenAporte: S1 = XYZW, S2 = XYWZ
Producción: 3
Explicación: Hay dos subsecuencias comunes de longitud 3 XYZ y XYW, y ninguna subsecuencia común. de longitud superior a 3.
Subsecuencia común más larga (LCS) mediante recursividad:
Genere todas las subsecuencias posibles y encuentre la más larga entre ellas que esté presente en ambas cadenas usando Siga los pasos a continuación para implementar la idea:
- Crea una función recursiva [digamos lcs() ].
- Verifique la relación entre los primeros caracteres de las cadenas que aún no están procesadas.
- Dependiendo de la relación, llame a la siguiente función recursiva como se mencionó anteriormente.
- Devuelve la longitud del LCS recibido como respuesta.
A continuación se muestra la implementación del enfoque recursivo:
C++C// A Naive recursive implementation of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n) // Driver code int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; int m = S1.size(); int n = S2.size(); cout << 'Length of LCS is ' << lcs(S1, S2, m, n); return 0; } // This code is contributed by rathbhupendra>Java// A Naive recursive implementation // of LCS problem #include int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j) // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b) ? a: b; } // Código del controlador int main() { char S1[] = 'BD'; carácter S2[] = 'ABCD'; intm = strlen(S1); int n = strlen(S2); int yo = 0, j = 0; // Llamada a función printf('La longitud de LCS es %d', lcs(S1, S2, i, j)); devolver 0; }>Pitón// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence { // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(String X, String Y, int m, int n) n == 0) return 0; if (X.charAt(m - 1) == Y.charAt(n - 1)) return 1 + lcs(X, Y, m - 1, n - 1); else return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n)); // Utility function to get max of 2 integers int max(int a, int b) { return (a>b) ? a: b; } // Código del controlador public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); Cadena S1 = 'AGGTAB'; Cadena S2 = 'GXTXAYB'; int m = S1.longitud(); int n = S2.longitud(); System.out.println('La longitud de LCS es' + ' ' + lcs.lcs(S1, S2, m, n)); } } // Este código es una contribución de Saket Kumar>C## A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>JavaScript// C# Naive recursive implementation of LCS problem using System; class GFG { // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n) if (m == 0 // Utility function to get max of 2 integers static int max(int a, int b) { return (a>b) ? a: b; } // Código del controlador public static void Main() { String S1 = 'AGGTAB'; Cadena S2 = 'GXTXAYB'; int m = S1.Longitud; int n = S2.Longitud; Console.Write('La longitud de LCS es' + ' ' + lcs(S1, S2, m, n)); } } // Este código es una contribución de Sam007>PHP>
ProducciónLength of LCS is 4>Complejidad del tiempo: o(2m+n)
Espacio Auxiliar: O(1)Subsecuencia común más larga (LCS) usando Memorización :
1. Subestructura óptima:
Ver para resolver la estructura de L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) estamos tomando la ayuda de las subestructuras de X[0 , 1,…, m-2], Y[0, 1,…, n-2], dependiendo de la situación (es decir, usándolos de manera óptima) para encontrar la solución del todo.
2. Subproblemas superpuestos:
Si utilizamos el enfoque recursivo anterior para cadenas BD y A B C D , obtendremos un árbol de recursividad parcial como se muestra a continuación. Aquí podemos ver que el subproblema L(BD, ABCD) se calcula más de una vez. Si se considera el árbol total, habrá varios subproblemas superpuestos.
L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
/ /
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)Acercarse: Debido a la presencia de estas dos propiedades, podemos utilizar la programación dinámica o la memorización para resolver el problema. A continuación se muestra el enfoque para la solución mediante recursividad.
- Crea una función recursiva. También cree una matriz 2D para almacenar el resultado de un estado único.
- Durante la llamada recursiva, si se llama al mismo estado más de una vez, podemos devolver directamente la respuesta almacenada para ese estado en lugar de calcular nuevamente.
A continuación se muestra la implementación del enfoque anterior:
C++Java// A Top-Down DP implementation // of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n, vector>& dp) { si (m == 0 || n == 0) devuelve 0; si (X[m - 1] == Y[n - 1]) devuelve dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); if (dp[m][n] != -1) { return dp[m][n]; } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Código del controlador int main() { char X[] = 'AGGTAB'; char Y[] = 'GXTXAYB'; intm = strlen(X); int n = strlen(Y); vector > dp(m + 1, vector (norte + 1, -1)); corte<< 'Length of LCS is ' << lcs(X, Y, m, n, dp); return 0; }> Pitón/*package whatever //do not write package name here */ import java.io.*; class GFG { // A Top-Down DP implementation of LCS problem // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n, int[][] dp) { if (m == 0 || n == 0) return 0; if (dp[m][n] != -1) return dp[m][n]; if (X.charAt(m - 1) == Y.charAt(n - 1)) { dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); return dp[m][n]; } dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); return dp[m][n]; } // Drivers code public static void main(String args[]) { String X = 'AGGTAB'; String Y = 'GXTXAYB'; int m = X.length(); int n = Y.length(); int[][] dp = new int[m + 1][n + 1]; for (int i = 0; i < m + 1; i++) { for (int j = 0; j < n + 1; j++) { dp[i][j] = -1; } } System.out.println('Length of LCS is ' + lcs(X, Y, m, n, dp)); } } // This code is contributed by shinjanpatra>C## A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>JavaScript/* C# Naive recursive implementation of LCS problem */ using System; class GFG { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ static int lcs(char[] X, char[] Y, int m, int n, int[, ] L) { if (m == 0 || n == 0) return 0; if (L[m, n] != -1) return L[m, n]; if (X[m - 1] == Y[n - 1]) { L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L); return L[m, n]; } L[m, n] = max(lcs(X, Y, m, n - 1, L), lcs(X, Y, m - 1, n, L)); return L[m, n]; } /* Utility function to get max of 2 integers */ static int max(int a, int b) { return (a>b) ? a: b; } public static void Main() { String s1 = 'AGGTAB'; Cadena s2 = 'GXTXAYB'; char[] X = s1.ToCharArray(); carbón[] Y = s2.ToCharArray(); int m = X.Longitud; int n = Y.Longitud; int[, ] L = nuevo int[m + 1, n + 1]; para (int i = 0; i<= m; i++) { for (int j = 0; j <= n; j++) { L[i, j] = -1; } } Console.Write('Length of LCS is' + ' ' + lcs(X, Y, m, n, L)); } } // This code is contributed by akshitsaxenaa09>/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) { if (m == 0 || n == 0) return 0; if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); if (dp[m][n] != -1) { return dp[m][n]; } return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) { dp[i] = new Array(n + 1).fill(-1); } console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>
ProducciónLength of LCS is 4>Complejidad del tiempo: O(m * n) donde myn son las longitudes de las cuerdas.
Espacio Auxiliar: O(m * n) Aquí se ignora el espacio de pila recursivo.Subsecuencia común más larga (LCS) usando de abajo hacia arriba (tabulación):
Podemos utilizar los siguientes pasos para implementar el enfoque de programación dinámica para LCS.
- Crear una matriz 2D DP[][] con filas y columnas iguales a la longitud de cada cadena de entrada más 1 [el número de filas indica los índices de T1 y las columnas indican los índices de T2 ].
- Inicialice la primera fila y columna de la matriz dp en 0.
- Iterar a través de las filas de la matriz dp, comenzando desde 1 (digamos usando iterador i ).
- Para cada i , itera todas las columnas de j = 1 an :
- Si T1[i-1] es igual a T2[j-1] , establezca el elemento actual de la matriz dp en el valor del elemento en ( dp[i-1][j-1] + 1 ).
- De lo contrario, establezca el elemento actual de la matriz dp en el valor máximo de dp[i-1][j] y dp[i][j-1] .
- Después de los bucles anidados, el último elemento de la matriz dp contendrá la longitud del LCS.
Vea la siguiente ilustración para una mejor comprensión:
Ilustración:
Digamos que las cuerdas son S1 = AGGTAB y S2 = GXTXAYB .
Primer paso: Inicialmente cree una matriz 2D (digamos dp[][]) de tamaño 8 x 7 cuya primera fila y primera columna estén llenas de 0.
Creando la tabla dp
Segundo paso: Atraviesa para i = 1. Cuando j se convierte en 5, S1[0] y S2[4] son iguales. Entonces el dp[][] se actualiza. Para los demás elementos, tome el máximo de dp[i-1][j] y dp[i][j-1]. (En este caso, si ambos valores son iguales, hemos utilizado flechas a las filas anteriores).
Llenando la fila número 1
shreya ghoshalTercer paso: Mientras se recorre para i = 2, S1[1] y S2[0] son iguales (ambos son 'G'). Entonces se actualiza el valor de dp en esa celda. El resto de elementos se actualizan según las condiciones.
Llenando la fila no. 2
cual es el tamaño de mi monitorCuarto paso: Para i = 3, S1[2] y S2[0] vuelven a ser iguales. Las actualizaciones son las siguientes.
Relleno de fila no. 3
Quinto paso: Para i = 4, podemos ver que S1[3] y S2[2] son iguales. Entonces dp[4][3] actualizado como dp[3][2] + 1 = 2.
Llenando la fila 4
Sexto paso: Aquí podemos ver que para i = 5 y j = 5 los valores de S1[4] y S2[4] son iguales (es decir, ambos son 'A'). Entonces dp[5][5] se actualiza en consecuencia y se convierte en 3.
Llenando la fila 5
Último paso: Para i = 6, vea que los últimos caracteres de ambas cadenas son iguales (son 'B'). Por lo tanto, el valor de dp[6][7] pasa a ser 4.
Llenando la última fila
Entonces obtenemos la longitud máxima de la subsecuencia común como 4 .
A continuación se muestra una implementación tabulada para el problema LCS.
C++Java// Dynamic Programming C++ implementation // of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) { // Initializing a matrix of size // (m+1)*(n+1) int L[m + 1][n + 1]; // Following steps build L[m+1][n+1] // in bottom up fashion. Note that // L[i][j] contains length of LCS of // X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) if (i == 0 } // L[m][n] contains length of LCS // for X[0..n-1] and Y[0..m-1] return L[m][n]; } // Driver code int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; int m = S1.size(); int n = S2.size(); // Function call cout << 'Length of LCS is ' << lcs(S1, S2, m, n); return 0; }>Pitón// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence { // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(String X, String Y, int m, int n) { int L[][] = new int[m + 1][n + 1]; // Following steps build L[m+1][n+1] in bottom up // fashion. Note that L[i][j] contains length of LCS // of X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) j == 0) L[i][j] = 0; else if (X.charAt(i - 1) == Y.charAt(j - 1)) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } return L[m][n]; } // Utility function to get max of 2 integers int max(int a, int b) { return (a>b) ? a: b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); Cadena S1 = 'AGGTAB'; Cadena S2 = 'GXTXAYB'; int m = S1.longitud(); int n = S2.longitud(); System.out.println('La longitud de LCS es' + ' ' + lcs.lcs(S1, S2, m, n)); } } // Este código es una contribución de Saket Kumar>C## Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>JavaScript// Dynamic Programming implementation of LCS problem using System; class GFG { // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n) { int[, ] L = new int[m + 1, n + 1]; // Following steps build L[m+1][n+1] // in bottom up fashion. // Note that L[i][j] contains length of // LCS of X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) j == 0) L[i, j] = 0; else if (X[i - 1] == Y[j - 1]) L[i, j] = L[i - 1, j - 1] + 1; else L[i, j] = max(L[i - 1, j], L[i, j - 1]); } return L[m, n]; } // Utility function to get max of 2 integers static int max(int a, int b) { return (a>b) ? a: b; } // Código del controlador public static void Main() { String S1 = 'AGGTAB'; Cadena S2 = 'GXTXAYB'; int m = S1.Longitud; int n = S2.Longitud; Console.Write('La longitud de LCS es' + ' ' + lcs(S1, S2, m, n)); } } // Este código es aportado por Sam007>PHP// Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers function max(a, b) { if (a>b) devolver a; de lo contrario regresar b; } // Devuelve la longitud de LCS para X[0..m-1], Y[0..n-1] function lcs(X, Y, m, n) { var L = new Array(m + 1); para(var i = 0; yo< L.length; i++) { L[i] = new Array(n + 1); } var i, j; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for(i = 0; i <= m; i++) { for(j = 0; j <= n; j++) j == 0) L[i][j] = 0; else if (X[i - 1] == Y[j - 1]) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } /* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */ return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>// Dynamic Programming C# // implementation of LCS problem function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1] // in bottom up fashion . // Note: L[i][j] contains length of // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) if ($i == 0 } // L[m][n] contains the length of // LCS of X[0..n-1] & Y[0..m-1] return $L[$m][$n]; } // Driver Code $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed // by Shivi_Aggarwal ?>>
ProducciónLength of LCS is 4>Complejidad del tiempo: O(m * n), que es mucho mejor que la complejidad temporal del peor de los casos de la implementación Naive Recursive.
Espacio Auxiliar: O(m * n) porque el algoritmo utiliza una matriz de tamaño (m+1)*(n+1) para almacenar la longitud de las subcadenas comunes.Subsecuencia común más larga (LCS) usando Bottom-Up (optimización del espacio):
- En el enfoque de tabulación anterior estamos usando L[i-1][j] y L[i][j], etc., aquí L[i-1] se referirá a la fila anterior de la matriz L y L[i] se referirá a la fila actual.
- Podemos optimizar el espacio utilizando dos vectores, uno es anterior y otro es actual.
- Cuando sale el bucle for interno, estamos inicializando el anterior igual al actual.
A continuación se muestra la implementación:
C++Java// Dynamic Programming C++ implementation // of LCS problem #include using namespace std; int longestCommonSubsequence(string& text1, string& text2) { int n = text1.size(); int m = text2.size(); // initializing 2 vectors of size m vectoranterior(m + 1, 0), cur(m + 1, 0); para (int idx2 = 0; idx2< m + 1; idx2++) cur[idx2] = 0; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // if matching if (text1[idx1 - 1] == text2[idx2 - 1]) cur[idx2] = 1 + prev[idx2 - 1]; // not matching else cur[idx2] = 0 + max(cur[idx2 - 1], prev[idx2]); } prev = cur; } return cur[m]; } int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; // Function call cout << 'Length of LCS is ' << longestCommonSubsequence(S1, S2); return 0; }> Pitón// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG { public static int longestCommonSubsequence(String text1, String text2) { int n = text1.length(); int m = text2.length(); // Initializing 2 arrays of size m int[] prev = new int[m + 1]; int[] cur = new int[m + 1]; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // If matching if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1)) cur[idx2] = 1 + prev[idx2 - 1]; // Not matching else cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]); } prev = Arrays.copyOf(cur, m + 1); } return cur[m]; } public static void main(String[] args) { String S1 = 'AGGTAB'; String S2 = 'GXTXAYB'; // Function call System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } }>C#def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>JavaScriptusing System; class Program { static int LongestCommonSubsequence(string text1, string text2) { int n = text1.Length; int m = text2.Length; // initializing 2 arrays of size m int[] prev = new int[m + 1]; int[] cur = new int[m + 1]; for (int idx2 = 0; idx2 < m + 1; idx2++) cur[idx2] = 0; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // if matching if (text1[idx1 - 1] == text2[idx2 - 1]) cur[idx2] = 1 + prev[idx2 - 1]; // not matching else cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]); } prev = cur; } return cur[m]; } static void Main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; // Function call Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2)); } }>function longestCommonSubsequence(text1, text2) { const n = text1.length; const m = text2.length; // Initializing two arrays of size m let prev = new Array(m + 1).fill(0); let cur = new Array(m + 1).fill(0); for (let idx2 = 0; idx2 < m + 1; idx2++) { cur[idx2] = 0; } for (let idx1 = 1; idx1 < n + 1; idx1++) { for (let idx2 = 1; idx2 < m + 1; idx2++) { // If characters match if (text1[idx1 - 1] === text2[idx2 - 1]) { cur[idx2] = 1 + prev[idx2 - 1]; } // If characters don't match else { cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]); } } // Update the 'prev' array prev = [...cur]; } return cur[m]; } // Main function function main() { const S1 = 'AGGTAB'; const S2 = 'GXTXAYB'; // Function call console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>
ProducciónLength of LCS is 4>Complejidad del tiempo: O(m * n), que sigue siendo el mismo.
Espacio Auxiliar: O(m) porque el algoritmo utiliza dos matrices de tamaño m.







