En este artículo, analizaremos el recorrido en orden en la estructura de datos.
Si queremos atravesar los nodos en orden ascendente, utilizamos el recorrido en orden. Los siguientes son los pasos necesarios para el recorrido en orden:
- Visita todos los nodos en el subárbol izquierdo.
- Visita el nodo raíz
- Visita todos los nodos en el subárbol derecho.
Las estructuras de datos lineales, como pila, matriz, cola, etc., solo tienen una forma de atravesar los datos. Pero en estructuras de datos jerárquicas como árbol, Hay varias formas de recorrer los datos. Aquí discutiremos otra forma de atravesar la estructura de datos del árbol, es decir, recorrido en orden.
Hay dos enfoques utilizados para el recorrido en orden:
limpieza de caché npm
- Recorrido en orden usando recursividad
- Recorrido en orden mediante un método iterativo
Una técnica de recorrido en orden sigue el Raíz izquierda derecha política. Aquí, Left Root Right significa que primero se atraviesa el subárbol izquierdo del nodo raíz, luego el nodo raíz y luego se atraviesa el subárbol derecho del nodo raíz. Aquí, el nombre del orden en sí sugiere que el nodo raíz se encuentra entre los subárboles izquierdo y derecho.
Discutiremos el recorrido en orden utilizando técnicas tanto recursivas como iterativas. Primero comencemos con el recorrido en orden usando recursividad.
Recorrido en orden mediante recursividad
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Ejemplo de recorrido en orden
Ahora, veamos un ejemplo de recorrido en orden. Será más fácil entender el procedimiento de recorrido en orden usando un ejemplo.
caja del interruptor java
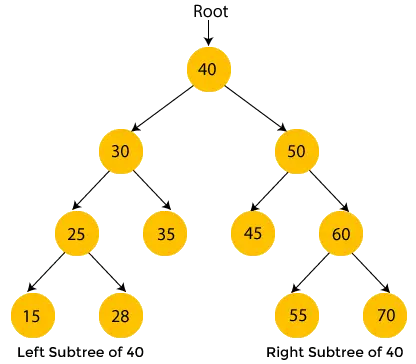
Los nodos de color amarillo aún no han sido visitados. Ahora, atravesaremos los nodos del árbol anterior utilizando un recorrido en orden.
- Aquí, 40 es el nodo raíz. Nos movemos al subárbol izquierdo de 40, que es 30, y también tiene el subárbol 25, por lo que volvemos a movernos al subárbol izquierdo de 25, que es 15. Aquí, 15 no tiene subárbol, entonces imprimir 15 y avanzar hacia su nodo padre, 25.
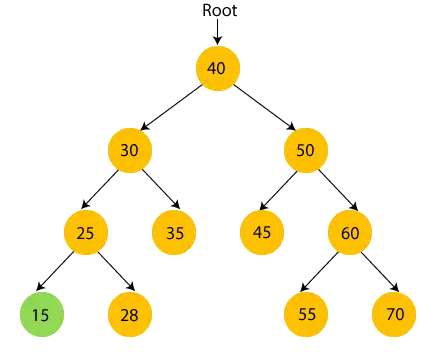
- Ahora, imprimir 25 y muévase al subárbol derecho de 25.
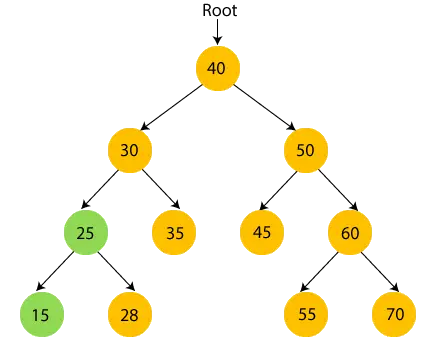
- Ahora, imprimir 28 y muévase al nodo raíz de 25, que es 30.
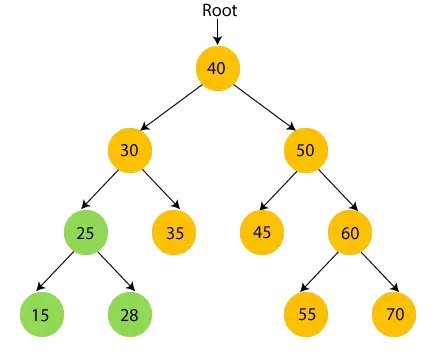
- Entonces, se visita el subárbol izquierdo de 30. Ahora, imprimir 30 y pasar al niño derecho de 30.
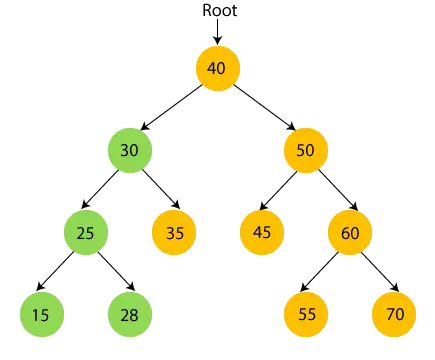
- Ahora, imprimir 35 y pasar al nodo raíz de 30.
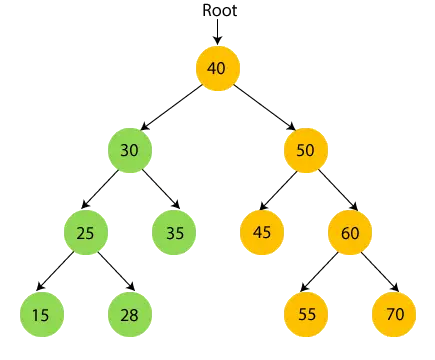
- Ahora, imprimir nodo raíz 40 y moverse a su subárbol derecho.
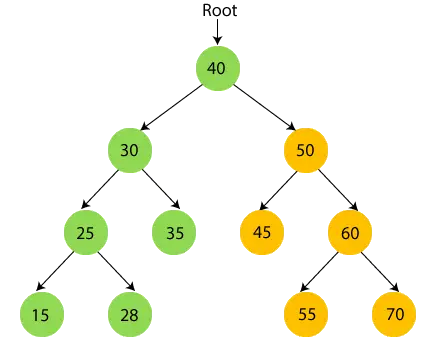
- Ahora recorra recursivamente el subárbol derecho de 40, que es 50.
50 tiene un subárbol, así que primero atraviesa el subárbol izquierdo de 50, que es 45. 45 no tiene hijos, por lo que imprimir 45 y pasar a su nodo raíz.
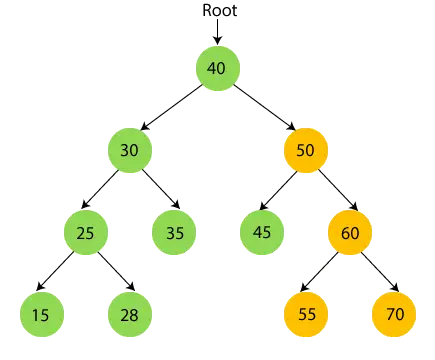
- Ahora imprimir 50 y muévase al subárbol derecho de 50 que es 60.
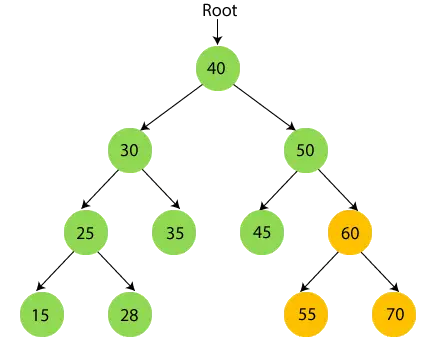
- Ahora recorra recursivamente el subárbol derecho de 50, que es 60. 60 tiene un subárbol, así que primero recorra el subárbol izquierdo de 60, que es 55. 55 no tiene hijos, por lo que imprimir 55 y pasar a su nodo raíz.
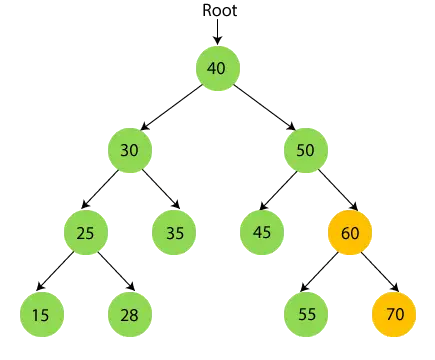
- Ahora imprimir 60 y muévase al subárbol derecho de 60 que es 70.
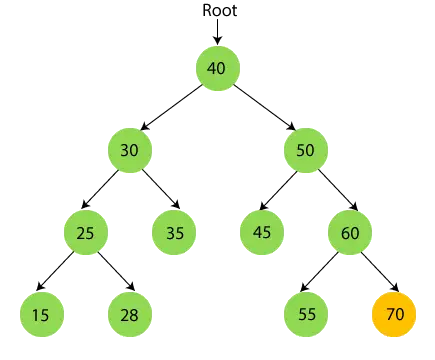
- Ahora imprimir 70.
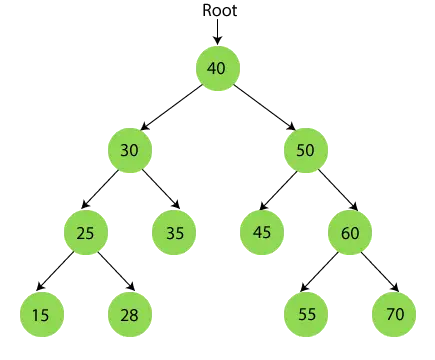
Una vez completado el recorrido en orden, el resultado final es:
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Complejidad del recorrido en orden
La complejidad temporal del recorrido de Inorder es En), donde 'n' es el tamaño del árbol binario.
Considerando que la complejidad espacial del recorrido en orden es O(1), si no consideramos el tamaño de la pila para las llamadas a funciones. De lo contrario, la complejidad espacial del recorrido en orden es Oh), donde 'h' es la altura del árbol.
Implementación del recorrido en orden
Ahora, veamos la implementación del recorrido en orden en diferentes lenguajes de programación.
Programa: Escriba un programa para implementar el recorrido en orden en lenguaje C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Producción
milivericket

Programa: Escriba un programa para implementar el recorrido en orden en C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Producción
programas de muestra java

Programa: Escriba un programa para implementar el recorrido en orden en Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Producción

Entonces, eso es todo sobre el artículo. Espero que el artículo le resulte útil e informativo.











