Menos que igual a es un concepto de desigualdad que significa que el término del lado izquierdo de la desigualdad no debe ser mayor que el término del lado derecho, es decir, el término izquierdo debe ser menor o como máximo igual al término derecho. El artículo cubre el concepto de menor o igual que en matemáticas, introduciendo el símbolo ≤ y su representación en una recta numérica. Incluye una tabla de símbolos matemáticos, problemas de práctica y respuestas a preguntas frecuentes sobre desigualdades.
Tabla de contenidos
comentarios java
- Menos que igual a firmar
- Símbolo menor o igual que
- Menor o igual que en una recta numérica
- Notaciones de símbolos de desigualdades
- Menor que igual a y mayor que igual a
Menos que igual a firmar
El signo menor que igual a se agrega en la imagen de abajo,
¿Qué es menor o igual que?
Menor o igual a significa que una cosa no es más que otra ni puede ser igual. Por ejemplo, si tenemos 2x – 3 ≤ 9, significa que 2 veces un número (x) menos 3 no es más que 9. Simplificando, si sumamos 3 a ambos lados, obtenemos 2x ≤ 12. Luego, al dividir ambos lados por 2, encontramos x ≤ 6. Entonces, dice que el número (x) puede ser 6 o menos, y sigue siendo cierto.
Además, consulte
- Menos que símbolo
- Signo igual
Menos que igual al ejemplo
Digamos que Juan y Pedro son dos amigos y la edad de Juan es menor o igual que la de Pedro. Significa que Juan es más joven o igual a la edad de Pedro. En otras palabras, podemos decir que Pedro es mayor o tiene al menos la misma edad que Juan.
Ahora, digamos que la edad de John es x años y la de Peter es 'y' años, entonces en la forma de la ecuación que involucra Menos que igual a podemos escribir esto como:
x ≤ y
dónde,
- x es la edad de John
- y es la edad de Peter
Símbolo menor o igual que
Símbolo de menor o igual a. es ≤
Se utiliza en matemáticas para comparar dos cantidades. Específicamente, cuando ves a ≤ b, significa que a es menor o igual que b. Este símbolo combina la idea de menor que (<) e igual a (=). Entonces, indica que el valor en el lado izquierdo del símbolo es menor o igual que el valor en el lado derecho. Esto ayuda a expresar relaciones entre números o expresiones matemáticas donde uno puede ser menor que el otro o igual a él.
Menor o igual que en una recta numérica
El concepto de menor o igual que en una recta numérica es una expresión matemática fundamental que se utiliza para comparar valores numéricos. En este contexto, significa que un número dado es menor o igual que otro número. Al representar esta relación en una recta numérica, se coloca un círculo cerrado (●) en el punto correspondiente al valor menor o igual. Por ejemplo, x ≤ 2 se representa de la siguiente manera en la recta numérica
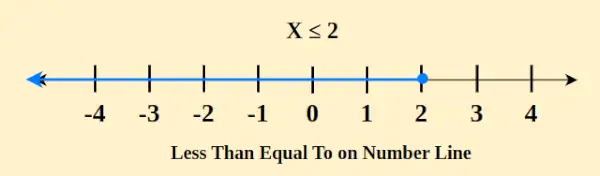
Además, una línea se extiende hacia la derecha desde este punto, abarcando todos los números mayores o iguales al valor designado. La inclusión de un círculo cerrado sirve para enfatizar que el punto final es parte de la comparación. Para ilustrar, si A ≤ B, el punto A puede ubicarse en o a la izquierda del punto B en la recta numérica, lo que indica que A es menor o igual que B, incluyendo la posibilidad de que A sea igual a B. Esta representación visual ayuda a comprender las magnitudes relativas de los valores comparados.
Notaciones de símbolos de desigualdades
Los diversos signos de desigualdad utilizados junto con su descripción se agregan a continuación:
| Notación de símbolos de desigualdades | |
|---|---|
| Descripción del símbolo | Notación de símbolos |
| signo mayor que | > |
| signo menor que | < |
| igual a firmar | = |
| No es igual a firmar | ≠ |
| Mayor menor o igual a | ≥ |
| Menos que o igual a | ≤ |
Menor que igual a y mayor que igual a
La comparación entre mayor que igual a y menor que igual a se menciona a continuación:
| Diferencia entre mayor que igual a y menor que igual a | ||
|---|---|---|
| Aspecto | Mayor que igual a | Menos que igual a |
| Significado | Indica el valor que es mayor o mínimo igual al valor dado | Indique el valor que es menor o como máximo igual al valor dado |
| Símbolo | ≥ | ≤ |
| Ejemplo | La edad del carnero es mayor que igual a 10 años. ⇒ Edad del carnero ≥ 10 | La edad de Rohan es inferior a 15 años. ⇒ Edad de Rohan ≤ 15 |
Lecturas relacionadas ,
- Mayor que menor que
- Mayor qué o igual a
- Desigualdades
Menos que igual a – Ejemplos
Ejemplo 1. Resuelve la desigualdad: 3x – 5 ≤ 10.
Solución:
Comience sumando 5 a ambos lados:
3x ≤ 15
Luego, divide por 3: x ≤ 5
Entonces la solución es x ≤ 5
Ejemplo 2. Resuelve la desigualdad: -2y + 7 ≤ 1.
Solución:
Resta 7 de ambos lados: -2y ≤ -6
Dividir por -2, recordando invertir el signo de desigualdad: y ≥ 3
La solución es y ≥ 3
Menos que igual a – Problemas de práctica
Pruebe los siguientes problemas de práctica basados en el concepto de menor que igual a
P1. Resuelve la desigualdad: 2y – 8 es menor o igual a 10.
P2. Si m es 6 y n es 3, determine si m al cuadrado menos 5 es menor o igual que 2n más 1.
P3. Resuelva para x: 3x más 7 es menor o igual a 22.
P4. Si q es un número positivo tal que 4q menos 6 es menor o igual a 14, encuentre los valores posibles para q.
P5. Determine el rango de valores de a que satisfacen la desigualdad 2a más 5 es menor o igual a 15.
Menos que igual a – Preguntas frecuentes
1. ¿Qué es menor o igual a?
Menor o igual a denota una relación entre dos valores, lo que implica que el primer valor es menor o igual que el segundo.
2. ¿Cómo se representa Menor que o Igual que en una recta numérica?
En una recta numérica, esta relación se representa visualmente colocando un círculo cerrado (●) en el número correspondiente al valor menor o igual y extendiendo una línea hacia la derecha, abarcando todos los números mayores o iguales a ese valor.
3. ¿Qué significa un círculo cerrado en la recta numérica?
El círculo cerrado enfatiza la inclusión del criterio de valoración en la comparación. Si, por ejemplo, A ≤ B, indica que el punto A está en el punto B o a la izquierda del mismo en la recta numérica, incluida la posibilidad de que A sea igual a B.
4. ¿Cuál es un ejemplo de cómo resolver una desigualdad menor o igual que?
Considere la desigualdad 2x – 3 ≤ 9. Si sumamos 3 a ambos lados, obtenemos 2x ≤ 12. Luego, al dividir ambos lados por 2, encontramos x ≤ 6. Por lo tanto, la solución a la desigualdad es x ≤ 6.
puntero en c
5. ¿Cómo se resuelven desigualdades que involucran menos o igual a?
Para resolver desigualdades como ax + b ≤ c, el enfoque habitual implica manipular la desigualdad mediante suma, resta, multiplicación o división para aislar la variable y determinar el rango de valores que satisfacen la desigualdad.
6. ¿Qué es el símbolo de menor que igual a y mayor que igual a?
Símbolo de menos que igual a es ≤ mientras que el símbolo de mayor que igual a es ≥.
