Árbol AVL:
El árbol AVL es un árbol de búsqueda binaria autoequilibrado ( hora estándar del este ) donde la diferencia entre las alturas de los subárboles izquierdo y derecho no puede ser mayor que uno para todos los nodos.
Ejemplo de árbol AVL:
El árbol anterior es AVL porque las diferencias entre las alturas de los subárboles izquierdo y derecho para cada nodo son menores o iguales a 1.
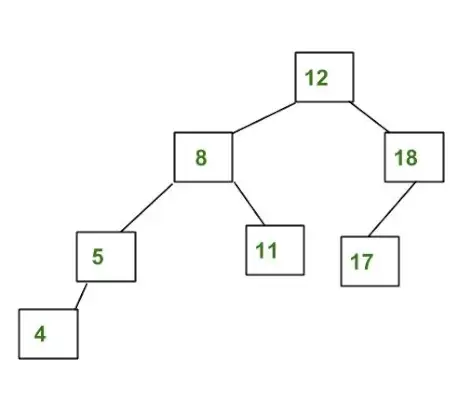
Ejemplo de un árbol que NO es un árbol AVL:

El árbol anterior no es AVL porque las diferencias entre las alturas de los subárboles izquierdo y derecho para 8 y 12 son mayores que 1.
¿Por qué árboles AVL?
La mayoría de las operaciones BST (por ejemplo, buscar, máximo, mínimo, insertar, eliminar, etc.) toman Oh) tiempo donde h es la altura del BST. El costo de estas operaciones puede llegar a ser En) para árbol binario sesgado . Si nos aseguramos de que la altura del árbol se mantenga O(log(n)) después de cada inserción y eliminación, entonces podemos garantizar un límite superior de O(log(n)) para todas estas operaciones. La altura de un árbol AVL es siempre O(log(n)) dónde norte es el número de nodos en el árbol.
Inserción en el árbol AVL:
Para asegurarnos de que el árbol dado siga siendo AVL después de cada inserción, debemos aumentar la operación de inserción BST estándar para realizar algún reequilibrio.
A continuación se presentan dos operaciones básicas que se pueden realizar para equilibrar un BST sin violar la propiedad BST (teclas (izquierda)
- Rotación izquierda
- Rotación derecha
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x / Right Rotation / x T3 - - - - - - ->T1 y / <- - - - - - - / T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>Práctica recomendada Inserción de árbol AVL ¡Pruébelo!
Pasos a seguir para la inserción:
Deje que el nodo recién insertado sea En
convertir cadena a int
- Realizar estándar hora estándar del este insertar para En .
- Empezando desde En , viaja hacia arriba y encuentra el primero. nodo desequilibrado . Dejar Con ser el primer nodo desequilibrado, y ser el niño de Con que viene en el camino de En a Con y X ser el nieto de Con que viene en el camino de En a Con .
- Vuelva a equilibrar el árbol realizando rotaciones apropiadas en el subárbol enraizado con Con. Puede haber 4 casos posibles que deben manejarse como x, y y Con Se puede organizar de 4 maneras.
- A continuación se muestran los 4 arreglos posibles:
- y es el hijo izquierdo de z y x es el hijo izquierdo de y (Caso izquierdo izquierdo)
- y es el hijo izquierdo de z y x es el hijo derecho de y (caso izquierdo derecho)
- y es el hijo derecho de z y x es el hijo derecho de y (Caso derecho correcto)
- y es el hijo derecho de z y x es el hijo izquierdo de y (caso derecho izquierdo)
A continuación se detallan las operaciones a realizar en los 4 casos mencionados anteriormente. En todos los casos, sólo necesitamos reequilibrar el subárbol enraizado con Con y el árbol completo se equilibra con la altura del subárbol (después de las rotaciones apropiadas) enraizado con Con vuelve a ser el mismo que era antes de la inserción.
1. Caso izquierdo izquierdo
T1, T2, T3 and T4 are subtrees. z y / / y T4 Right Rotate (z) x z / - - - - - - - - ->/ / x T3 T1 T2 T3 T4 / T1 T2>
2. Caso izquierdo derecho
z z x / / / y T4 Left Rotate (y) x T4 Right Rotate(z) y z / - - - - - - - - ->/ - - - - - - - -> / / T1 x y T3 T1 T2 T3 T4 / / T2 T3 T1 T2>
3. Caso correcto
z y / / T1 y Left Rotate(z) z x / - - - - - - - ->/ / T2 x T1 T2 T3 T4 / T3 T4>
4. Caso Derecha Izquierda
z z x / / / T1 y Right Rotate (y) T1 x Left Rotate(z) z y / - - - - - - - - ->/ - - - - - - - -> / / x T4 T2 y T1 T2 T3 T4 / / T2 T3 T3 T4>
Ilustración de la inserción en el árbol AVL





Acercarse:
La idea es utilizar la inserción BST recursiva; después de la inserción, obtenemos punteros a todos los antepasados uno por uno de abajo hacia arriba. Por lo tanto, no necesitamos un puntero principal para subir. El código recursivo viaja hacia arriba y visita todos los antepasados del nodo recién insertado.
Siga los pasos que se mencionan a continuación para implementar la idea:
- realizar lo normal Inserción de BST.
- El nodo actual debe ser uno de los ancestros del nodo recién insertado. Actualizar el altura del nodo actual.
- Obtener el factor de equilibrio (altura del subárbol izquierdo – altura del subárbol derecho) del nodo actual.
- Si el factor de equilibrio es mayor que 1, entonces el nodo actual está desequilibrado y estamos en el Caso izquierdo izquierdo o caso izquierdo derecho . Para comprobar si es caso izquierdo izquierdo o no, compare la clave recién insertada con la clave en el raíz del subárbol izquierdo .
- Si el factor de equilibrio es menor que -1 , entonces el nodo actual está desequilibrado y estamos en el caso Derecha Derecha o Derecha-Izquierda. Para comprobar si es el caso Derecha Derecha o no, compare la clave recién insertada con la clave en la raíz del subárbol derecho.
A continuación se muestra la implementación del enfoque anterior:
C++14
// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->altura;> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a: b;> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->clave = clave;> >node->izquierda = NULO;> >node->derecha = NULO;> >node->altura = 1;>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->izquierda;> >Node *T2 = x->bien;> > >// Perform rotation> >x->derecha = y;> >y->izquierda = T2;> > >// Update heights> >y->altura = max(altura(y->izquierda),> >height(y->derecha)) + 1;> >x->altura = max(altura(x->izquierda),> >height(x->derecha)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->bien;> >Node *T2 = y->izquierda;> > >// Perform rotation> >y->izquierda = x;> >x->derecha = T2;> > >// Update heights> >x->altura = max(altura(x->izquierda),> >height(x->derecha)) + 1;> >y->altura = max(altura(y->izquierda),> >height(y->derecha)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->izquierda) - altura (N->derecha);> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->izquierda = insertar(nodo->izquierda, clave);> >else> if> (key>nodo->clave)> >node->derecha = insertar(nodo->derecha, clave);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->altura = 1 + max(altura(nodo->izquierda),> >height(node->bien));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && tecla izquierda->tecla)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->derecha->tecla)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && tecla> nodo->izquierda->tecla)> >{> >node->izquierda = rotación izquierda(nodo->izquierda);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->clave)> >{> >node->derecha = rotaciónderecha(nodo->derecha);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->izquierda); preOrder(raíz->derecha); } } // Código del controlador int main() { Nodo *root = NULL; /* Construyendo el árbol mostrado en la figura anterior */ root = insert(root, 10); raíz = insertar(raíz, 20); raíz = insertar(raíz, 30); raíz = insertar(raíz, 40); raíz = insertar(raíz, 50); raíz = insertar(raíz, 25); /* El árbol AVL construido sería 30 / 20 40 / 10 25 50 */ cout<< 'Preorder traversal of the ' 'constructed AVL tree is
'; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> |
>
>
C
// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->altura;> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a: b;> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->clave = clave;> >node->izquierda = NULO;> >node->derecha = NULO;> >node->altura = 1;>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->izquierda;> >struct> Node *T2 = x->bien;> > >// Perform rotation> >x->derecha = y;> >y->izquierda = T2;> > >// Update heights> >y->altura = max(altura(y->izquierda),> >height(y->derecha)) + 1;> >x->altura = max(altura(x->izquierda),> >height(x->derecha)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->bien;> >struct> Node *T2 = y->izquierda;> > >// Perform rotation> >y->izquierda = x;> >x->derecha = T2;> > >// Update heights> >x->altura = max(altura(x->izquierda),> >height(x->derecha)) + 1;> >y->altura = max(altura(y->izquierda),> >height(y->derecha)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->izquierda) - altura (N->derecha);> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->izquierda = insertar(nodo->izquierda, clave);> >else> if> (key>nodo->clave)> >node->derecha = insertar(nodo->derecha, clave);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->altura = 1 + max(altura(nodo->izquierda),> >height(node->bien));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && tecla izquierda->tecla)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->derecha->tecla)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && tecla> nodo->izquierda->tecla)> >{> >node->izquierda = rotación izquierda(nodo->izquierda);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->tecla)> >{> >node->derecha = rotaciónderecha(nodo->derecha);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->llave);> >preOrder(root->izquierda);> >preOrder(root->bien);> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is
'>);> >preOrder(root);> > >return> 0;> }> |
>
que meses son q3
>
Java
// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>b) ? a: b;> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>nodo.clave) nodo.derecha = insertar(nodo.derecha, clave); else // No se permiten claves duplicadas return node; /* 2. Actualizar la altura de este nodo ancestro */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Obtenga el factor de equilibrio de este nodo ancestro para comprobar si este nodo se desequilibró */ int balance = getBalance(node); // Si este nodo se desequilibra, entonces // hay 4 casos Izquierda Izquierda Caso if (equilibrio> 1 && key return rightRotate(nodo); // Derecha Derecha Caso if (equilibrio<-1 && key>nodo.derecha.clave) return leftRotate(nodo); // Caso izquierdo derecho if (saldo> 1 && clave> nodo.izquierda.clave) { nodo.izquierda = leftRotate(nodo.izquierda); volver a la derechaRotar(nodo); } // Caso derecho izquierdo si (saldo<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> |
>
>
Python3
# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 y la clave regresa self.rightRotate(root) # Caso 2 - Derecha Derecha si hay equilibrio<-1 and key>root.right.val: return self.leftRotate(root) # Caso 3 - Izquierda Derecha si balance> 1 y clave> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root) ) # Caso 4 - Derecha Izquierda si hay equilibrio<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> |
>
milivericket
>
C#
// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>b) ? a: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>nodo.clave) nodo.derecha = insertar(nodo.derecha, clave); else // No se permiten claves duplicadas return node; /* 2. Actualizar la altura de este nodo ancestro */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Obtenga el factor de equilibrio de este nodo ancestro para comprobar si este nodo se desequilibró */ int balance = getBalance(node); // Si este nodo se desequilibra, entonces hay // 4 casos Izquierda Izquierda Caso if (equilibrio> 1 && clave return rightRotate(nodo); // Derecha Derecha Caso if (equilibrio nodo.right.key) return leftRotate(nodo) ; // Caso izquierdo derecho if (saldo> 1 && tecla> nodo.izquierda.clave) { nodo.izquierda = leftRotate(node.left); return rightRotate(nodo);<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> |
>
>
JavaScript
> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>b ? a: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>nodo.clave) nodo.derecho = this.insert(nodo.derecho, clave); // No se permiten claves duplicadas else return node; /* 2. Actualizar la altura de este nodo ancestro */ node.height = 1 + this.max(this.height(node.left), this.height(node.right)); /* 3. Obtenga el factor de equilibrio de este nodo ancestro para comprobar si este nodo se desequilibró */ var balance = this.getBalance(node); // Si este nodo se desequilibra, entonces hay // 4 casos Izquierda Izquierda Caso if (equilibrio> 1 && clave devuelve this.rightRotate(nodo); // Derecha Derecha Caso si (equilibrio nodo.right.key) devuelve esto. leftRotate(nodo); // Caso izquierdo derecho if (saldo> 1 && clave> nodo.izquierda.clave) { nodo.izquierda = this.leftRotate(nodo.izquierda); return this.rightRotate(nodo); Caso izquierdo si (saldo<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> |
>
>Producción
Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>
Análisis de complejidad
Complejidad del tiempo: O(log(n)), para inserción
Espacio Auxiliar: O(1)
Las operaciones de rotación (rotación a la izquierda y a la derecha) toman un tiempo constante ya que allí solo se cambian unos pocos punteros. Actualizar la altura y obtener el factor de equilibrio también lleva un tiempo constante. Por lo tanto, la complejidad temporal de la inserción AVL sigue siendo la misma que la de la inserción BST, que es O(h), donde h es la altura del árbol. Dado que el árbol AVL está equilibrado, la altura es O (Logn). Entonces, la complejidad temporal de la inserción AVL es O (Logn).
Comparación con el árbol rojo negro:
El árbol AVL y otros árboles de búsqueda con equilibrio automático como Red Black son útiles para realizar todas las operaciones básicas en un tiempo O (log n). Los árboles AVL están más equilibrados en comparación con los árboles Rojo-Negro, pero pueden provocar más rotaciones durante la inserción y eliminación. Entonces, si su aplicación implica muchas inserciones y eliminaciones frecuentes, entonces se deben preferir los árboles Rojo Negro. Y si las inserciones y eliminaciones son menos frecuentes y la búsqueda es la operación más frecuente, entonces se debe preferir el árbol AVL al Red Black Tree.
La siguiente es la publicación para eliminar en AVL Tree:
Árbol AVL | Conjunto 2 (Eliminación)
