El método codicioso es una de las estrategias como Divide y conquistarás utilizadas para resolver los problemas. Este método se utiliza para resolver problemas de optimización. Un problema de optimización es un problema que exige resultados máximos o mínimos. Entendamos a través de algunos términos.
El método Greedy es el enfoque más simple y directo. No es un algoritmo, pero es una técnica. La función principal de este enfoque es que la decisión se toma sobre la base de la información actualmente disponible. Cualquiera que sea la información actual presente, la decisión se toma sin preocuparse por el efecto de la decisión actual en el futuro.
prueba la estructura de datos
Esta técnica se utiliza básicamente para determinar la solución factible que puede ser óptima o no. La solución factible es un subconjunto que satisface los criterios dados. La solución óptima es la solución que es la mejor y más favorable del subconjunto. En el caso de factible, si más de una solución satisface los criterios dados, esas soluciones se considerarán factibles, mientras que la solución óptima es la mejor solución entre todas las soluciones.
Características del método codicioso
Las siguientes son las características de un método codicioso:
- Para construir la solución de manera óptima, este algoritmo crea dos conjuntos donde un conjunto contiene todos los elementos elegidos y otro conjunto contiene los elementos rechazados.
- Un algoritmo codicioso toma buenas decisiones locales con la esperanza de que la solución sea factible u óptima.
Componentes del algoritmo codicioso
Los componentes que se pueden utilizar en el algoritmo codicioso son:
cadena json java
Aplicaciones del algoritmo codicioso
- Se utiliza para encontrar el camino más corto.
- Se utiliza para encontrar el árbol de expansión mínimo utilizando el algoritmo de prim o el algoritmo de Kruskal.
- Se utiliza en una secuenciación de trabajos con fecha límite.
- Este algoritmo también se utiliza para resolver el problema de la mochila fraccionaria.
Pseudocódigo del algoritmo codicioso
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Lo anterior es el algoritmo codicioso. Inicialmente, a la solución se le asigna un valor cero. Pasamos la matriz y el número de elementos en el algoritmo codicioso. Dentro del bucle for, seleccionamos los elementos uno por uno y comprobamos si la solución es factible o no. Si la solución es factible, entonces realizamos la unión.
Entendamos a través de un ejemplo.
Supongamos que hay un problema 'P'. Quiero viajar de A a B como se muestra a continuación:
PAG: A → B
El problema es que tenemos que recorrer este viaje de A a B. Hay varias soluciones para ir de A a B. Podemos ir de A a B caminar, coche, bicicleta, tren, avión , etc. Hay una restricción en el viaje de que tenemos que recorrer este viaje dentro de las 12 horas. Si voy en tren o en avión, puedo cubrir esta distancia en 12 horas. Hay muchas soluciones a este problema, pero sólo dos soluciones satisfacen la restricción.
java convierte caracteres a cadenas
Si decimos eso tenemos que cubrir el trayecto al mínimo coste. Esto significa que tenemos que recorrer esta distancia la mínima posible, por lo que este problema se conoce como problema de minimización. Hasta ahora tenemos dos soluciones viables, una por tren y otra por aire. Dado que viajar en tren supondrá un coste mínimo, es una solución óptima. Una solución óptima es también la solución factible, pero proporcionando el mejor resultado para que esa solución sea la solución óptima con el mínimo coste. Sólo habría una solución óptima.
El problema que requiere un resultado mínimo o máximo se conoce como problema de optimización. El método codicioso es una de las estrategias utilizadas para resolver los problemas de optimización.
Desventajas de usar el algoritmo codicioso
El algoritmo codicioso toma decisiones basadas en la información disponible en cada fase sin considerar el problema más amplio. Por lo tanto, puede existir la posibilidad de que la solución codiciosa no proporcione la mejor solución para cada problema.
1 a 100 número romano
Sigue la elección del óptimo local en cada etapa con la intención de encontrar el óptimo global. Entendamos a través de un ejemplo.
Considere el gráfico que se muestra a continuación:
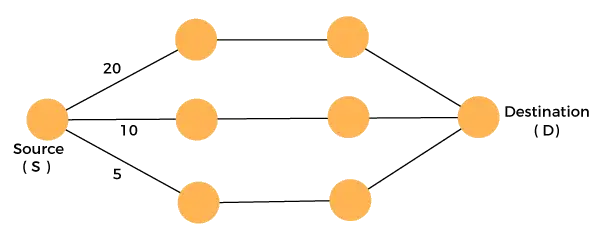
Tenemos que viajar desde el origen hasta el destino con el mínimo coste. Dado que tenemos tres soluciones factibles con rutas de costos como 10, 20 y 5, 5 es la ruta de costo mínimo, por lo que es la solución óptima. Este es el óptimo local y de esta manera encontramos el óptimo local en cada etapa para calcular la solución óptima global.
