Los problemas de regresión y clasificación probabilística se pueden resolver mediante el proceso gaussiano (GP), una técnica de aprendizaje supervisado. Dado que cada proceso gaussiano puede considerarse como una generalización de dimensión infinita de procesos multivariados distribuciones gaussianas , el término gaussiano aparece en el nombre. En esta publicación analizaremos los procesos gaussianos para la regresión, que también se conocen como regresión del proceso gaussiano (GPR). Numerosos problemas del mundo real en los campos de la ciencia de materiales, la química, la física y la biología se han resuelto con el uso de GPR.

Tabla de contenidos

• Regresión del proceso gaussiano (GPR)
• Conceptos clave de la regresión del proceso gaussiano (GPR)
• Concepto matemático de regresión del proceso gaussiano (GPR)
• Implementación del proceso gaussiano en Python

Regresión del proceso gaussiano (GPR)

La regresión del proceso gaussiano (GPR) es una técnica de regresión no paramétrica potente y flexible que se utiliza en aprendizaje automático y Estadísticas . Es particularmente útil cuando se trata de problemas que involucran datos continuos, donde la relación entre las variables de entrada y la salida no se conoce explícitamente o puede ser compleja. GPR es un enfoque bayesiano que puede modelar la certeza en las predicciones, lo que lo convierte en una herramienta valiosa para diversas aplicaciones, incluida la optimización, el pronóstico de series temporales y más. GPR se basa en el concepto de proceso gaussiano, que es una colección de variables aleatorias, cualquier número finito de las cuales tiene una distribución gaussiana conjunta. Se puede considerar un proceso gaussiano como una distribución de funciones.

Conceptos clave de la regresión del proceso gaussiano (GPR)

Proceso Gaussain

Un modelo probabilístico no paramétrico llamado Proceso gaussiano (GP) se utiliza en estadística y aprendizaje automático para regresión, clasificación y cuantificación de incertidumbre. Representa un grupo de variables aleatorias, cada una de las cuales tiene una distribución gaussiana conjunta y puede tener un número finito. Los GP son una técnica versátil y eficaz para modelar relaciones intrincadas en datos y producir pronósticos con incertidumbre relacionada.

Características de los procesos gaussianos :

• Naturaleza no paramétrica : Los médicos de cabecera pueden adaptarse a la complejidad de los datos porque no dependen de un número determinado de parámetros del modelo.
• Predicciones probabilísticas : Las predicciones de los médicos de cabecera se pueden cuantificar porque ofrecen predicciones como distribuciones de probabilidad.
• Interpolación y suavizado : Los GP son útiles para datos ruidosos o muestreados de forma irregular porque son buenos para suavizar datos ruidosos e interpolar entre puntos de datos.
• Marginación de hiperparámetros : Al eliminar el requisito de ajustes explícitos de hiperparámetros, marginan los hiperparámetros, lo que simplifica el modelo.

Función media

El valor predicho de la función que se modela en cada punto de entrada está representado por el función media en Procesos Gaussianos (GP). Funciona como una presunción fundamental con respecto a la estructura de datos subyacente. La función media con frecuencia se establece en cero de forma predeterminada, no necesariamente, y puede modificarse según las propiedades de los datos o la experiencia en el dominio. Al influir en la tendencia central de los pronósticos, ayuda a los médicos generales a identificar patrones o tendencias en los datos. Los médicos de cabecera proporcionan predicciones probabilísticas que contienen incertidumbre, así como estimaciones puntuales al incluir la función media.

Función de covarianza (núcleo)

El función de covarianza , también conocida como función kernel, mide qué tan similares son los puntos de datos de entrada entre sí en los procesos gaussianos (GP). Es fundamental para caracterizar el comportamiento del modelo GP, afectando la selección de funciones de la distribución anterior. La función de covarianza mide similitudes por pares para determinar la correlación entre los valores de la función. Los médicos de cabecera pueden adaptarse a una amplia gama de patrones de datos, desde tendencias suaves hasta estructuras complejas, porque diferentes funciones del núcleo capturan diferentes tipos de correlaciones. El rendimiento del modelo puede verse muy afectado por la selección del núcleo.

Distribuciones anteriores

El distribución previa , en Procesos Gaussianos (GP), es nuestra comprensión de las funciones antes de la observación de cualquier dato. Por lo general, se describe mediante una función de covarianza (kernel) y una función media. Mientras que la función de covarianza describe la similitud o correlación entre los valores de la función en varios puntos de entrada, la función media codifica nuestras expectativas previas. Los médicos de cabecera lo utilizan de antemano para crear una distribución de funciones. En los médicos de cabecera, se pueden seleccionar antecedentes para representar la incertidumbre de los datos, integrar el conocimiento del dominio o indicar la fluidez.

Distribuciones posteriores

Procesos gaussianos posterior distribution muestra nuestras suposiciones revisadas sobre funciones después de la observación de datos. Reúne la probabilidad de los datos dada la función y la distribución anterior. La regresión posterior en GP ofrece una distribución sobre funciones que más se acerca a los datos observados. Al permitir predicciones probabilísticas y la cuantificación de la incertidumbre, la distribución posterior refleja el equilibrio entre las creencias previas almacenadas en la distribución anterior y la información proporcionada por los datos.

Concepto matemático de regresión del proceso gaussiano (GPR)

Para las tareas de regresión, se emplea un modelo de aprendizaje automático probabilístico no paramétrico llamado regresión del proceso gaussiano (GP). Al modelar interacciones complejas y ambiguas entre variables de entrada y salida, es una herramienta potente. Se supone que una distribución gaussiana multivariada produce los puntos de datos en la regresión GP y el objetivo es inferir esta distribución.

nombre de caracteres especiales

El modelo de regresión GP tiene la siguiente expresión matemática. Supongamos x₁, X₂,…..,X_norteson los puntos de datos de entrada, donde x pertenecen a números reales (-2,-1,0,1…), (x_iepsilon r)

Supongamos que y₁, y_{2 ,}……., y_norteson los valores de salida, donde y_ipertenece al número real (y_iepsilon r)

El modelo de regresión GP supone que un proceso gaussiano con una función media (mu ) y la función de covarianza (k) proporciona la función f que conecta las entradas con las salidas.

Entonces, en un conjunto de ubicaciones de prueba x*, la distribución de f viene dada por:

f(x^*) ∼ N(mu(x^*), k(x^*, x^*))

Normalmente, las funciones del núcleo se utilizan para definir la función media y la función de covarianza. A modo de ilustración, el núcleo exponencial al cuadrado que se emplea con frecuencia se describe como:

k(x_{i},x_{j}) = sigma^2 exp(-frac{||x_{i} – x_{j}||^2}{2l^2})

Dónde,

• k(x_{i}, x_{j}) = La función del núcleo está representada por esto y calcula la correlación o similitud entre dos puntos de datos de entrada, x_iyx_j.
• sigma^2 = El parámetro de varianza del kernel es este. Establece la escala o extensión vertical de la función kernel. Regula la fuerza con la que se correlacionan los puntos de datos. Una mayorsigma^2 produce una función kernel con mayor varianza.
• exp: La función exponencial es responsable de elevar e a la potencia del argumento.
• ||x_{i} – x_{j}||^2 : La diferencia entre los puntos de datos de entrada, x_iyx_j, es la distancia euclidiana al cuadrado. Se mide la separación geométrica entre los puntos en el espacio característico.
• yo²: Esta es una representación de la escala de longitud del grano o longitud característica. Regula la velocidad a la que se deteriora la función del núcleo a medida que los puntos de datos están más separados. Una l más baja hace que el núcleo se degrade más rápido.

El modelo de regresión GP aplica la inferencia bayesiana para determinar la distribución de f que es más probable que haya producido los datos dado un conjunto de datos de entrenamiento (x, y). Para ello se debe calcular la distribución posterior de f dados los datos, que se define de la siguiente manera:

p(f|x,y) =frac x,f)p(f) x)

convertir de cadena a entero java

donde la probabilidad marginal de los datos es p(y|x), la distribución previa de f es p(f) y la probabilidad de los datos dada la función f es (y|x,f).

Después de conocer la distribución posterior de f, el modelo calcula la distribución predictiva posterior para hacer predicciones en puntos de prueba adicionales x*. Se puede definir de la siguiente manera:

p(f^*|x^*, y,x) = int p(f^*|x^*, f), p(f|y,x)df

Dónde,

• p(f^*|x*, y, x) = Esto muestra, dados los datos de entrenamiento y y x, la probabilidad condicional de los valores de función predichos f^*en un nuevo punto de entrada x^*Para decirlo de otra manera, es la distribución de probabilidad sobre todos los valores potenciales de la función en el nuevo sitio de entrada x^*, condicionado a los datos observados y y sus ubicaciones de entrada coincidentes x.
• int p(f^*|x^*, f)p(f|y,x)df = Se emplea una integral en esta sección de la ecuación para determinar la probabilidad condicional. La integral abarca todos los valores potenciales de la función f.
• p(f^*|x^*, f) = Esta es la distribución de probabilidad condicional de los valores esperados de la función f^*en x^*, dados los valores de la función f en algunas ubicaciones intermedias.
• p(f|y,x) = Dados los datos observados (y) y sus ubicaciones de entrada (x), esta es la distribución de probabilidad condicional de los valores de la función (f).

Para tareas como la toma de decisiones consciente de la incertidumbre y el aprendizaje activo, esta distribución ofrece una medida de la incertidumbre de la predicción, que puede resultar útil.

lista ordenada java

Pasos en la regresión del proceso gaussiano

• Recopilación de datos : Reúna los pares de datos de entrada y salida para su problema de regresión.
• Elija una función del kernel : Seleccione una función de covarianza (núcleo) adecuada que se adapte a su problema. La elección del núcleo influye en la forma de las funciones que GPR puede modelar.
• Optimización de parámetros : Estime los hiperparámetros de la función del núcleo maximizando la probabilidad de los datos. Esto se puede hacer utilizando técnicas de optimización como el descenso de gradiente.
• Predicción: Dada una nueva entrada, utilice el modelo GPR entrenado para hacer predicciones. GPR proporciona tanto la media prevista como la incertidumbre asociada (varianza).

Implementación del proceso de regresión gaussiano (GPR)

Producción:

En este código, primero genere algunos puntos de datos de muestra con ruido agregado, luego defina un núcleo RBF y cree un Regresor del proceso gaussiano con eso. El modelo se entrena con los datos de entrenamiento y se utiliza para hacer predicciones sobre los datos de prueba. Finalmente, los resultados se visualizan con un gráfico que muestra los datos de entrenamiento, la media prevista y el intervalo de confianza del 95%.

Implementación del proceso gaussiano en Python

Aprendizaje científico

Este código importa las bibliotecas necesarias para la regresión del proceso gaussiano (GPR) en Python; estos son ciencia ficción para funciones de álgebra lineal, NumPy para operaciones numéricas, y Matplotlib para visualización de datos. Para asegurarse de que sea compatible con los paquetes necesarios, además verifica la versión de Python y la imprime, junto con las versiones de NumPy y scikit-learn (sklearn).

Selección de granos

Producción:

[RBF(longitud_escala=1),
RacionalCuadrático(alfa=1, longitud_escala=1),
ExpSineSquared(longitud_escala=1, periodicidad=10),
Productopunto(sigma_0=1) ** 2,
Materna(escala_longitud=1, nu=1.5)]

El código especifica el número de sitios de prueba (n) e inicializa un Semilla aleatoria . Para mostrar los núcleos elegidos, genera una lista de varias funciones del núcleo e imprime la lista.

sumador completo sumador

Comparación y visualización de kernels

Producción:

FBR

gp.kernel_RBF(longitud_escala=1,93)
gp.log_marginal_likelihood: -3.444937833462133
---------------------------------------------------

Racional Cuadrática

gp.kernel_ RationalQuadratic(alfa=1e+05, longitud_escala=1,93)
gp.log_marginal_likelihood: -3.4449718909150966
--------------------------------------------------

ExpSenoAl Cuadrado

gp.kernel_ ExpSineSquared(longitud_escala=0.000524, periodicidad=2.31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
--------------------------------------------------

Producto escalar

gp.kernel_ DotProduct(sigma_0=0.998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------

Materno

gp.kernel_ Matern(longitud_escala=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------

El código comienza recorriendo las diversas funciones del kernel enumeradas en la lista kernel_. Se crea un regresor de proceso gaussiano (gp) utilizando el núcleo particular para cada núcleo. Para el Proceso Gaussiano, esto establece la estructura de covarianza. Para evaluar la distribución anterior se establece un conjunto de puntos de entrada de prueba denominado x_test, con valores que van de -5 a 5. Este conjunto de puntos se transforma en un vector columna.

cadena de formato java

Utilizando el método gp.predict, la media (mu_prior) y la desviación estándar (sd_prior) de la distribución anterior se determinan en cada punto de prueba. Los valores de desviación estándar se solicitan mediante la opción return_std=True. gp.sample_y (x_test, 3) se utiliza para obtener tres muestras de funciones de la distribución anterior.

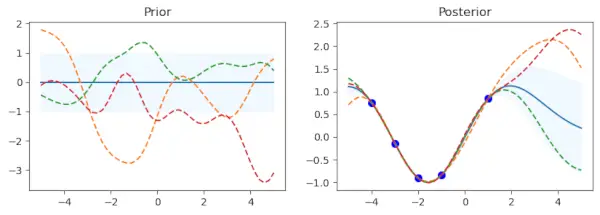
El primer subgráfico muestra la media de la distribución anterior, con la desviación estándar representada por un área sombreada. Las muestras se superponen como líneas discontinuas, mientras que la media se muestra como una línea continua. Hay una trama secundaria llamada Prior. Hay un conjunto definido de puntos de datos de entrenamiento (x_train) y valores objetivo (y_train) que los acompañan. El modelo del proceso gaussiano se ajusta utilizando estos puntos (gp.fit(x_train, y_train)). Cinco puntos de datos con sus correspondientes valores senos conforman los datos de entrenamiento en este código.

Después de la fase de ajuste de los datos de entrenamiento, el procedimiento calcula la media de la distribución posterior (mu_post) y la desviación estándar (sd_post) para los mismos puntos de prueba (x_test). gp.sample_y(x_test, 3) también se utiliza para producir muestras de funciones a partir de la distribución posterior. El segundo subgráfico superpone las funciones muestreadas como líneas de puntos y muestra la media de la distribución posterior, sombreada con la desviación estándar. En azul están los puntos de datos de entrenamiento. La subtrama tiene el nombre de Posterior.

Para ver los gráficos anterior y posterior del kernel actual y obtener una comprensión visual del comportamiento del modelo, llame a la función plt.show() de Matplotlib.

El código muestra detalles sobre el kernel actual, como gp.kernel_, que indica el kernel actual que se está utilizando, y gp.log_marginal_likelihood (gp.kernel_.theta), que proporciona la probabilidad marginal logarítmica del modelo que utiliza el núcleo actual, después de cada conjunto de gráficos anteriores y posteriores.

Ventajas de la regresión del proceso gaussiano (GPR)

La regresión del proceso gaussiano (GPR) tiene una serie de beneficios en una variedad de aplicaciones:

• GPR proporciona un marco probabilístico para la regresión, lo que significa que no sólo proporciona estimaciones puntuales sino que también proporciona estimaciones de incertidumbre para las predicciones.
• Es muy flexible y puede capturar relaciones complejas en los datos.
• GPR se puede adaptar a diversas aplicaciones, incluida la previsión de series temporales, la optimización y la optimización bayesiana.

Desafíos de la regresión del proceso gaussiano (GPR)

• GPR puede resultar costoso desde el punto de vista computacional cuando se trata de grandes conjuntos de datos, ya que se requiere la inversión de una matriz de covarianza.
• La elección de la función del núcleo y sus hiperparámetros puede afectar significativamente el rendimiento del modelo.

Buenos ejemplos de aplicaciones GPR

• Predicción del precio de las acciones: GPR se puede utilizar para modelar y predecir los precios de las acciones, teniendo en cuenta la volatilidad y la incertidumbre de los mercados financieros.
• Experimentos informáticos: GPR es útil para optimizar simulaciones complejas modelando las relaciones entrada-salida e identificando los parámetros más influyentes.
• Detección de anomalías: GPR se puede aplicar a la detección de anomalías, donde identifica patrones inusuales en datos de series temporales mediante la captura de distribuciones de datos normales.

Conclusión

En conclusión, la regresión del proceso gaussiano es una herramienta valiosa para el análisis y la predicción de datos en situaciones en las que comprender la incertidumbre en las predicciones es esencial. Al aprovechar el modelado probabilístico y las funciones del núcleo, GPR puede proporcionar resultados precisos e interpretables. Sin embargo, es crucial considerar el costo computacional y la necesidad de aportes de expertos al implementar GPR en la práctica.