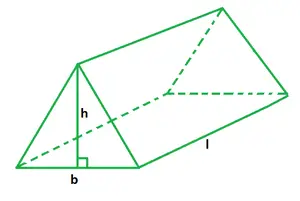
Un prisma es una figura sólida tridimensional con dos extremos idénticos. Se compone de lados planos, bases similares y secciones transversales iguales. Sus caras son paralelogramos o rectángulos sin base. Un prisma que tiene tres caras rectangulares y dos bases triangulares paralelas se llama prisma triangular. Las bases triangulares están unidas por caras laterales paralelas entre sí.
Fórmula del volumen de un prisma triangular
El volumen de un prisma triangular se define como el espacio dentro de él o el espacio que ocupa. Conocer el área de la base y la altura de un prisma triangular es todo lo que se necesita para calcular su volumen. El volumen de un prisma triangular es igual al producto del área de la base por la altura del prisma, también conocido como longitud del prisma. El área de la base de un prisma triangular es igual a la mitad del producto de la base triangular por su altura.
Fórmula
V = (1/2) × b × h × l
dónde,
b es la base triangular,
h es la altitud del prisma,
l es la longitud del prisma.
Problemas de muestra
Problema 1. Encuentra el volumen de un prisma triangular si su base mide 6 cm, su altura es 8 cm y su longitud es 12 cm.
Solución:
Tenemos b = 6, h = 8 y l = 12.
encapsulación javaUsando la fórmula que tenemos,
V = (1/2) × b × h × l
= (1/2) × 6 × 8 × 12
registro numeroso= 3 × 8 × 12
= 288 pies cúbicos cm
Problema 2. Encuentra el volumen de un prisma triangular si su base mide 5 cm, su altura es 7 cm y su longitud es 8 cm.
Solución:
Tenemos b = 5, h = 7 y l = 8.
Usando la fórmula que tenemos,
V = (1/2) × b × h × l
= (1/2) × 5 × 7 × 8
= 5 × 7 × 4
= 140 pies cúbicos cm
Problema 3. Encuentra la longitud del prisma triangular si su base mide 6 cm, su altura es 9 cm y su volumen es 98 pies cúbicos. cm.
Solución:
Tenemos b = 6, h = 9 y V = 98.
Usando la fórmula que tenemos,
V = (1/2) × b × h × l
=> 98 = (1/2) × 6 × 9 × l
diferencia entre dos cadenas python=> 196 = 27 litros
=> l = 196/27
=> largo = 7,25 cm
Problema 4. Encuentra la altura del prisma triangular si su base mide 8 cm, su longitud es 14 cm y su volumen es 504 pies cúbicos. cm.
Solución:
Tenemos b = 8, l = 14 y V = 504.
Usando la fórmula que tenemos,
V = (1/2) × b × h × l
=> 504 = (1/2) × 8 × h × 14
=> 504 = 56h
=> h = 504/56
=> altura = 9 cm
Problema 5. Encuentra el área de la base del prisma triangular si su longitud es de 18 cm, su altura es de 10 cm y su volumen es de 450 pies cúbicos. cm.
Solución:
Tenemos l = 18, h = 10 y V = 450.
Usando la fórmula para el volumen tenemos,
java agregar a la matrizV = (1/2) × b × h × l
=> 450 = (1/2) × b × 10 × 18
=> 450 = 90b
=> b = 450/90
=> ancho = 5 cm
Por tanto, el área de la base triangular es,
A = (1/2) × b × h
= (1/2) × 5 × 10
= 25 cm2
