La trigonometría es una rama importante de las matemáticas que se ocupa de la relación entre los ángulos y las longitudes de los lados de un triángulo rectángulo. Las seis razones o funciones trigonométricas son seno, coseno, tangente, cosecante y secante, y una razón trigonométrica es una razón entre los lados de un triángulo rectángulo. Las funciones seno, coseno y tangente son tres funciones trigonométricas importantes, ya que las otras tres, es decir, las funciones cosecante, secante y cotangente, son funciones recíprocas de las funciones seno, coseno y tangente, respectivamente.
- sin θ = lado opuesto/hipotenusa
- cos θ = Lado adyacente/Hipotenusa
- tan θ = Lado opuesto/Lado adyacente
- cosec θ = hipotenusa/lado opuesto
- sec θ = hipotenusa/lado adyacente
- cuna θ = Lado adyacente/Lado opuesto
La función tangente es una de las 6 funciones trigonométricas utilizadas en fórmulas de trigonometría .
Tabla de contenidos
Fórmula tangente
La tangente de un ángulo en un triángulo rectángulo es la relación entre la longitud del lado opuesto y la longitud del lado adyacente al ángulo dado. Escribimos una función tangente como tan. Consideremos un triángulo rectángulo XYZ y uno de sus ángulos agudos es θ. Un lado opuesto es el lado opuesto al ángulo θ y el lado adyacente es el lado adyacente al ángulo θ.
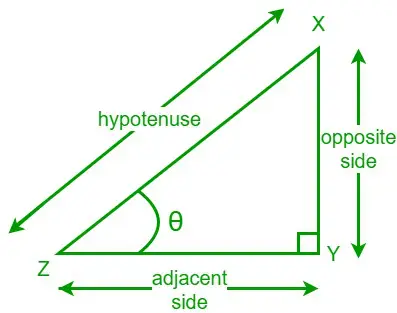
Ahora, la fórmula de la tangente para el ángulo θ dado es,
tan θ = Lado opuesto/Lado adyacente
Algunas fórmulas tangentes básicas
Función tangente en cuadrantes
La función tangente es positiva en el primer y tercer cuadrante y negativa en el segundo y cuarto cuadrante.
- tan (2π + θ) = tan θ (1callecuadrante)
- tan (π – θ) = – tan θ (2Dakota del Nortecuadrante)
- tan (π + θ) = tan θ (3tercerocuadrante)
- tan (2π – θ) = – tan θ (4thcuadrante)
Función tangente como función negativa
La función tangente es una función negativa ya que la tangente de un ángulo negativo es la negativa de un ángulo tangente positivo.
tan (-θ) = – tan θ
Función tangente en términos de función seno y coseno
La función tangente en términos de funciones seno y coseno se puede escribir como,
tan θ = sen θ/cos θ
Sabemos que tan θ = Lado opuesto/Lado adyacente
Ahora, divide tanto el numerador como el denominador por la hipotenusa.
tan θ = (Lado opuesto/Hipotenusa)/(Lado adyacente/Hipotenusa)
Sabemos que sen θ = lado opuesto/hipotenusa
cos θ = lado adyacente/hipotenusa
Por lo tanto, tan θ = sin θ/cos θ
Función tangente en términos de función seno
La función tangente en términos de la función seno se puede escribir como,
tan θ = sin θ/(√1 – sin 2 i)
Lo sabemos,
tan θ = sen θ/cos θ
entidad relacional
De las identidades pitagóricas, tenemos,
sin2θ + porque2θ = 1
porque2θ = 1 – pecado2i
cos θ = √(1 – sin2i)
Por lo tanto, tan θ = sin θ/(√1 – sin2i)
Función tangente en términos de función coseno
La función tangente en términos de la función coseno se puede escribir como,
tan θ = (√1 -cos 2 i)/porque yo
Lo sabemos,
tan θ = sen θ/cos θ
De las identidades pitagóricas, tenemos,
sin2θ + porque2θ = 1
sin2θ = 1 – porque2i
sin θ = √(1 – cos2i)
Hence, tan θ = (√1 – cos2i)/porque yo
Función tangente en términos de función cotangente
La función tangente en términos de la función cotangente se puede escribir como,
tan θ = 1/cuna θ
o
tan θ = cot (90° – θ) (o) cot (π/2 – θ)
Función tangente en términos de función cosecante
La función tangente en términos de la función cosecante se puede escribir como,
tan θ = 1/√(cosec 2 yo – 1)
De las identidades pitagóricas, tenemos,
cosec2θ – cuna2θ = 1
cuna2θ = cosec2yo – 1
cuna θ = √(cosec2yo – 1)
Lo sabemos,
tan θ = 1/cuna θ
Por tanto, tan θ = 1/√(cosec2yo – 1)
Función tangente en términos de función secante
La función tangente en términos de la función secante se puede escribir como,
tan θ = √sec 2 yo – 1
De las identidades pitagóricas, tenemos,
segundo2θ – tan2θ = 1
tan θ = segundo2yo – 1
Por lo tanto, tan θ = √(seg2yo – 1)
Función tangente en términos de doble ángulo
La función tangente para un ángulo doble es,
tan 2θ = (2 tan θ)/(1 – tan 2 i)
Función tangente en términos de ángulo triple
La función tangente para un ángulo triple es,
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 tan 2 i)
Función tangente en términos de medio ángulo
La función tangente para un medio ángulo es,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / (sen θ)
Función tangente en términos de suma y resta de dos ángulos
Las fórmulas de suma y diferencia para una función tangente son,
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Tabla de razones trigonométricas
| Ángulo (en grados) | Ángulo (en radianes) | pecado yo | porque θ | tan θ = sen θ/cos θ | cosec θ | segundo θ | cuna yo |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Indefinido | 1 | Indefinido |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 2/√3 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 ¿Qué es un nombre de usuario? | 2/√3 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = indefinido | 1 | Indefinido | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 2/√3 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(2/√3) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Indefinido | -1 | Indefinido |
Ejemplo resuelto de fórmulas tangentes
Ejemplo 1: Encuentre el valor de tan θ si sen θ = 2/5 y θ es el ángulo del primer cuadrante.
Solución:
Dado,
autómatas finitos no deterministas
- pecado θ = 2/5
De las identidades pitagóricas tenemos,
sin2θ + porque2θ = 1
porque2θ = 1 – pecado2θ = 1 – (2/5)2
porque2θ = 1 – (4/5) = 21/25
porque θ = ±√21/5
Dado que θ es el ángulo del primer cuadrante, cos θ es positivo.
porque θ = √21/5
Lo sabemos,
tan θ = sen θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21 /21
Entonces, el valor de tan θ cuando sin θ = 2/5 y θ está en el primer cuadrante es (2√21) /(21)
Ejemplo 2: Encuentre el valor de tan x si sec x = 13/12 y x es el ángulo del cuarto cuadrante.
Solución:
Dado, seg x = 13/12
De las identidades pitagóricas, tenemos,
segundo2x – tan2x = 1
tan2x = segundos2x-1= (13/12)2– 1
tan2x = (169/144) – 1 = 25/144
tan x = ± 5/12
Dado que x es el ángulo del cuarto cuadrante, tan x es negativo.
tan x = – 5/12
Por eso, tan x = – 5/12
Ejemplo 3: Si tan X = 2/3 y tan Y = 1/2, ¿cuál es el valor de tan (X + Y)?
Solución:
Dado,
tan X = 2/3 and tan Y = 1/2
Lo sabemos,
tan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Por eso, tan (X + Y) = 7/4
Ejemplo 4: Calcule la función tangente si los lados adyacentes y opuestos de un triángulo rectángulo miden 4 cm y 7 cm, respectivamente.
Solución:
Dado,
Lado adyacente = 4 cm
Lado opuesto = 7 cm
Lo sabemos,
tan θ = Lado opuesto/Lado adyacente
tan θ = 7/4 = 1.75
Por eso, tan θ = 1.75
Ejemplo 5: Un hombre mira la torre de un reloj en un ángulo de 60° con respecto a la parte superior de la torre, cuya altura es de 100 m. ¿Cuál es la distancia entre el hombre y el pie de la torre?
Solución:
Dado,
Altura de la torre = 100 m y θ = 60°
Sea la distancia entre el hombre y el pie de la torre = d
Tenemos,
tan θ = Lado opuesto/Lado adyacente
tan 60° = 100/d
√3 = 100/d [Since, tan 60° = √3]
re = 100/√3
Por tanto, la distancia entre el hombre y el pie de la torre es 100/√3
Ejemplo 6: Encuentre el valor de tan θ si sin θ = 7/25 y sec θ = 25/24.
Solución:
Dado,
pecado θ = 7/25
segundo θ = 25/24
Lo sabemos,
seg θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Tenemos,
tan θ = sen θ/cos θ
= (7/25)/(24/25)
= 7/24
Por eso, tan θ = 7/24
Ejemplo 7: Encuentre el valor de tan θ si cosec θ = 5/3 y θ es el ángulo del primer cuadrante.
Solución:
Dado, cosec θ = 5/3
De las identidades pitagóricas, tenemos,
10 ml a onzascosec2θ – cuna2θ = 1
cuna2θ = cosec2yo – 1
cuna θ = (5/3)2– 1 = (25/9) – 1 = 16/9
cuna θ = ±√16/9 = ± 4/3
Dado que θ es el ángulo del primer cuadrante, tanto la función cotangente como la tangente son positivas.
cuna θ = 4/3
Lo sabemos,
cuna θ = 1/tan θ
4/3 = 1/tan θ
tan θ = 3/4
Por eso, tan θ = 3/4
Ejemplo 8: Encuentre tan 3θ si sen θ = 3/7 y θ es el ángulo del primer cuadrante.
Solución :
Dado, sen θ = 12/13
De las identidades pitagóricas tenemos,
sin2θ + porque2θ = 1
porque2θ = 1 – pecado2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
porque θ = ±√25/169 = ±5/13
Dado que θ es el ángulo del primer cuadrante, cos θ es positivo.
porque θ = 5/13
Lo sabemos,
tan θ = sen θ/cos θ
= (12/25)/(5/13) = 12/5
Por tanto, tan θ = 12/5
Ahora sabemos que
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

