COMPONENTES FUERTEMENTE CONECTADOS - TECHCODEVIEW.COM

Componentes fuertemente conectados (SCC) son un concepto fundamental en la teoría de grafos y los algoritmos. En una gráfica dirigida, una Componente fuertemente conectado es un subconjunto de vértices donde se puede acceder a cada vértice del subconjunto desde todos los demás vértices del mismo subconjunto atravesando los bordes dirigidos. Encontrar el SCC de un gráfico puede proporcionar información importante sobre la estructura y la conectividad del gráfico, con aplicaciones en diversos campos, como análisis de redes sociales, rastreo web y enrutamiento de redes . Este tutorial explorará la definición, las propiedades y los algoritmos eficientes para identificar componentes fuertemente conectados en estructuras de datos de gráficos.

subprograma

Tabla de contenidos

¿Qué son los componentes fuertemente conectados (SCC)?
¿Por qué son importantes los componentes fuertemente conectados (SCC)?
Diferencia entre componentes conectados y fuertemente conectados (SCC)
¿Por qué no se puede utilizar el método DFS convencional para encontrar componentes fuertemente conectados?
Conexión de dos componentes fuertemente conectados mediante un borde unidireccional
Enfoque de fuerza bruta para encontrar componentes fuertemente conectados
Enfoque eficiente para encontrar componentes fuertemente conectados (SCC)

1. Algoritmo de Kosaraju:
2. Algoritmo de Tarjan:

Conclusión

¿Qué son los componentes fuertemente conectados (SCC)?

A componente fuertemente conectado de un gráfico dirigido es un subgrafo máximo donde cada par de vértices es mutuamente alcanzable. Esto significa que para dos nodos cualesquiera A y B en este subgrafo, hay un camino de A a B y un camino de B a A.

Por ejemplo: El siguiente gráfico tiene dos componentes fuertemente conectados {1,2,3,4} y {5,6,7} ya que hay un camino desde cada vértice a todos los demás vértices en el mismo componente fuertemente conectado.

Componente fuertemente conectado

¿Por qué son importantes los componentes fuertemente conectados (SCC)?

Comprender los SCC es crucial para diversas aplicaciones, como por ejemplo:

Análisis de red : Identificar grupos de nodos estrechamente interconectados.
Optimización de rastreadores web : Determinar partes del gráfico web que están estrechamente vinculadas.
Resolución de dependencia : En software, comprender qué módulos son interdependientes.

Diferencia entre componentes conectados y fuertemente conectados ( SCC)

Conectividad en un gráfico no dirigido Se refiere a si dos vértices son accesibles entre sí o no. Se dice que dos vértices están conectados si hay un camino entre ellos. Mientras tanto Fuertemente conectado es aplicable sólo a grafos dirigidos . Un subgrafo de un grafo dirigido se considera un Componentes fuertemente conectados (CCS) si y solo si para cada par de vértices A y B , existe un camino desde A a B y un camino desde B a A . Veamos por qué el método dfs estándar para encontrar componentes conectados en un gráfico no se puede utilizar para determinar componentes fuertemente conectados.

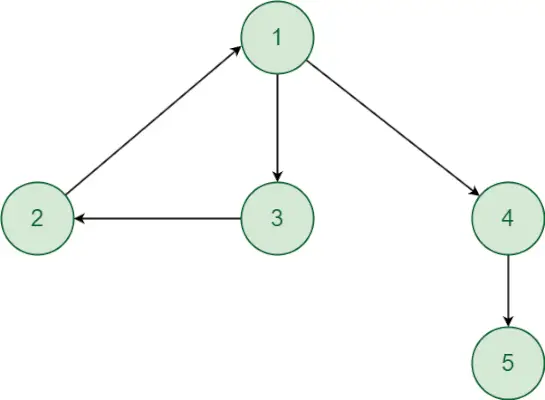
Considere el siguiente gráfico:

Python __nombre__

Ahora, comencemos un dfs llame desde el vértice 1 para visitar otros vértices.

¿Por qué no se puede utilizar el método DFS convencional para encontrar los componentes fuertemente conectados?

Se pueden alcanzar todos los vértices desde el vértice 1. Pero los vértices 1 y 5,6,7 no pueden estar en el mismo componente fuertemente conectado porque no hay un camino dirigido desde el vértice 5,6 o 7 al vértice 1. El gráfico tiene dos vértices fuertemente componentes conectados {1,2,3,4} y {5,6,7}. Por tanto, el método dfs convencional no se puede utilizar para encontrar los componentes fuertemente conectados.

Conexión de dos componentes fuertemente conectados mediante un borde unidireccional

Dos componentes conectados diferentes se convierten en un solo componente si se agrega una arista entre un vértice de un componente y un vértice de otro componente. Pero este no es el caso de los componentes fuertemente conectados. Dos componentes fuertemente conectados no se convierten en un solo componente fuertemente conectado si solo hay un borde unidireccional de un SCC a otro SCC.

tutorial de hadoop

unidrawio-(2)

Enfoque de fuerza bruta para encontrar componentes fuertemente conectados

El método simple será para cada vértice i (que no es parte de ningún componente fuerte) encontrar los vértices que serán parte del componente fuertemente conectado que contiene el vértice i. Dos vértices i y j estarán en el mismo componente fuertemente conectado si hay un camino dirigido desde el vértice i al vértice j y viceversa.

Entendamos el enfoque con la ayuda del siguiente ejemplo:

Comenzando con el vértice 1. Hay un camino desde el vértice 1 al vértice 2 y viceversa. De manera similar, existe un camino desde el vértice 1 al vértice 3 y viceversa. Entonces, los vértices 2 y 3 estarán en el mismo componente fuertemente conectado que el vértice 1. Aunque hay un camino dirigido desde el vértice 1 al vértice 4 y al vértice 5. Pero no hay un camino dirigido desde el vértice 4,5 al vértice 1, por lo que el vértice 4 y 5 no estarán en el mismo componente fuertemente conectado que el vértice 1. Por lo tanto, los vértices 1, 2 y 3 forman un componente fuertemente conectado.
Para los vértices 2 y 3, ya se ha determinado el componente fuertemente conectado.
Para el vértice 4, hay un camino desde el vértice 4 al vértice 5 pero no hay un camino desde el vértice 5 al vértice 4. Por lo tanto, los vértices 4 y 5 no estarán en el mismo componente fuertemente conectado. Por lo tanto, Vertex 4 y Vertex 5 serán parte de un componente único fuertemente conectado.
Por lo tanto, habrá 3 componentes fuertemente conectados {1,2,3}, {4} y {5}.

A continuación se muestra la implementación del enfoque anterior:

C++

 #include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vector & vis) { // Si el nodo actual es el destino, devuelve verdadero if (curr == des) { devuelve verdadero;  } vis[curr] = 1;  for (auto x: adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  }  }  }  falso retorno;  } // Para saber si existe una ruta desde el origen hasta // el destino bool isPath(int src, int des, vector>& adj) { vector vis(adj.tamaño() + 1, 0);  devolver dfs(src, des, adj, vis);  } // Función para devolver todos los // componentes fuertemente conectados de un gráfico.  vector> buscarSCC(int n, vector>& a) { // Almacena todos los componentes fuertemente conectados.  vector> ans;  // Almacena si un vértice es parte de cualquier vector de componente fuertemente // conectado is_scc(n + 1, 0);  vector> adj(norte + 1);  para (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector cc;  scc.push_back(yo);  para (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> bordes { { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vector> ans = obj.findSCC(V, bordes);  corte<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>

Java

 import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, lista vis) { // Si el nodo actual es el destino, devuelve verdadero if (curr == des) { devuelve verdadero;  } vis.set(curr, 1);  for (int x: adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  }  }  }  falso retorno;  } // Para saber si hay una ruta desde el origen hasta // el destino booleano isPath(int src, int des, List> adj) { Lista vis = nueva ArrayList(adj.size() + 1);  para (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> buscarSCC(int n, Lista> a) { // Almacena todos los componentes fuertemente conectados.  Lista> respuesta = nueva ArrayList();  // Almacena si un vértice es parte de cualquier // Lista de componentes fuertemente conectados is_scc = nueva ArrayList(n + 1);  para (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = nueva ArrayList();  para (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List borde: a) { adj.get(edge.get(0)).add(edge.get(1));  } // Atravesando todos los vértices para (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = nueva ArrayList();  scc.add(i);  para (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> bordes = nueva ArrayList();  bordes.add(new ArrayList(List.of(1, 3)));  bordes.add(new ArrayList(List.of(1, 4)));  bordes.add(new ArrayList(List.of(2, 1)));  bordes.add(new ArrayList(List.of(3, 2)));  bordes.add(new ArrayList(List.of(4, 5)));  Lista> ans = obj.findSCC(V, bordes);  System.out.println('Los componentes fuertemente conectados son:');  para (lista x : respuesta) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Este código es aportado por shivamgupta310570>

Pitón

 class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570>

 using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, lista vis) { // Si el nodo actual es el destino, devuelve verdadero if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x en adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  }  }  }  falso retorno;  } // Para saber si existe una ruta desde el origen al destino public bool IsPath(int src, int des, List> adj) { var show = nueva Lista (adj.Cuenta + 1);  para (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> BuscarSCC(int n, Lista> a) { // Almacena todos los componentes fuertemente conectados var ans = nueva Lista>();  // Almacena si un vértice es parte de cualquier componente fuertemente conectado var isScc = nueva lista (norte + 1);  para (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(norte + 1);  para (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } para (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  para (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> bordes = nueva lista> { nueva lista { 1, 3 }, nueva lista { 1, 4 }, nueva lista { 2, 1 }, nueva lista { 3, 2 }, nueva lista { 4, 5 } };  Lista> ans = obj.FindSCC(V, bordes);  Console.WriteLine('Los componentes fuertemente conectados son:');  foreach (var x en ans) { foreach (var y en x) { Console.Write(y + ' ');  } Consola.WriteLine();  } } } // Este código es aportado por shivamgupta310570>

JavaScript

 class GFG {  // Function to reach the destination using DFS  dfs(curr, des, adj, vis) {  // If the current node is the destination, return true  if (curr === des) {  return true;  }  vis[curr] = 1;  for (let x of adj[curr]) {  if (!vis[x]) {  if (this.dfs(x, des, adj, vis)) {  return true;  }  }  }  return false;  }  // Check whether there is a path from source to destination  isPath(src, des, adj) {  const vis = new Array(adj.length + 1).fill(0);  return this.dfs(src, des, adj, vis);  }  // Function to find all strongly connected components of a graph  findSCC(n, a) {  // Stores all strongly connected components  const ans = [];  // Stores whether a vertex is part of any Strongly Connected Component  const is_scc = new Array(n + 1).fill(0);  const adj = new Array(n + 1).fill().map(() =>[]);  para (sea i = 0; i< a.length; i++) {  adj[a[i][0]].push(a[i][1]);  }  // Traversing all the vertices  for (let i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not part of any SCC,  // insert it into a new SCC list and check  // for other vertices that can be part of this list.  const scc = [i];  for (let j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push(j);  }  }  // Insert the SCC containing vertex i into the final list.  ans.push(scc);  }  }  return ans;  } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [  [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) {  console.log(x.join(' ')); } // This code is contributed by shivamgupta310570>

Producción

Strongly Connected Components are: 1 2 3 4 5>

Complejidad del tiempo: O (n * (n + m)), porque para cada par de vértices estamos comprobando si existe un camino entre ellos.
Espacio auxiliar: O(N)

cómo cerrar el modo desarrollador

Enfoque eficiente para encontrar componentes fuertemente conectados (SCC)

Para encontrar SCC en un gráfico, podemos usar algoritmos como Algoritmo de Kosaraju o Algoritmo de Tarjan . Exploremos estos algoritmos paso a paso.

1. Algoritmo de Kosaraju :

El algoritmo de Kosaraju consta de dos fases principales:

Realizar una búsqueda en profundidad (DFS) en el gráfico original :
- Primero hacemos un DFS en el gráfico original y registramos los tiempos de finalización de los nodos (es decir, el momento en que el DFS termina de explorar un nodo por completo).
Realizar DFS en el gráfico transpuesto :
- Luego invertimos la dirección de todos los bordes del gráfico para crear el gráfico transpuesto.
- A continuación, realizamos un DFS en el gráfico transpuesto, considerando los nodos en orden decreciente de sus tiempos de finalización registrados en la primera fase.
- Cada recorrido DFS en esta fase nos dará un SCC.

Aquí hay una versión simplificada del algoritmo de Kosaraju:

DFS en el gráfico original : Récord de tiempos de finalización.
Transponer el gráfico : Invierta todos los bordes.
DFS en gráfico transpuesto : Procese los nodos en orden de tiempos de finalización decrecientes para encontrar SCC.

2. Algoritmo de Tarjan :

El algoritmo de Tarjan es más eficiente porque encuentra SCC en un solo pase DFS usando una pila y algo de contabilidad adicional:

Recorrido DFS : Durante el DFS, mantenga un índice para cada nodo y el índice más pequeño (valor de enlace bajo) que se puede alcanzar desde el nodo.
Pila : realiza un seguimiento de los nodos actualmente en la pila de recursividad (parte del SCC actual que se está explorando).
Identificación de SCC : Cuando el valor de enlace bajo de un nodo es igual a su índice, significa que hemos encontrado un SCC. Extraiga todos los nodos de la pila hasta llegar al nodo actual.

Aquí hay un resumen simplificado del algoritmo de Tarjan:

Inicializarindex>a 0.
Para cada nodo no visitado, realice DFS.
- Establezca el índice del nodo y el valor de enlace bajo.
- Empuje el nodo hacia la pila.
- Para cada nodo adyacente, realice DFS si no se visita o actualice el valor de enlace bajo si está en la pila.
- Si el valor de enlace bajo del nodo es igual a su índice, saque los nodos de la pila para formar un SCC.

Conclusión

Comprender y encontrar componentes fuertemente conectados en un gráfico dirigido es esencial para muchas aplicaciones en informática. Kosaraju's y Tarjano Los algoritmos son formas eficientes de identificar SCC, cada una con su propio enfoque y ventajas. Al dominar estos conceptos, podrá analizar y optimizar mejor la estructura y el comportamiento de redes complejas.