La forma estándar de una parábola es y = ax²+ bx + c donde a, byc son números reales y a no es igual a cero. Una parábola se define como el conjunto de todos los puntos de un plano que equidistan de una recta fija y de un punto fijo del plano.

En este artículo, entenderemos en detalle qué es una parábola, la ecuación estándar de una parábola, ejemplos relacionados y otros.

Tabla de contenidos

• ¿Qué es una parábola?
• Ecuación de una parábola
• Ecuaciones generales de una parábola
• Ecuaciones estándar de una parábola
• Partes de una parábola
• Ejemplos de ecuación de una parábola

¿Qué es una parábola?

Una parábola es una sección cónica definida como el conjunto de todos los puntos equidistantes de un punto llamado foco y una recta llamada directriz. Las ecuaciones estándar para una parábola dependen de su orientación (dirección de apertura) y posición.

Ecuación de una parábola

La ecuación de la parábola se puede escribir en forma estándar o general y ambas se agregan a continuación:

Ecuaciones generales de una parábola

La ecuación general de una parábola es,

y = 4a(x – h) ² +k

(o)

x = 4a(y – k) ² +h

Donde (h, k) es el vértice de una parábola.

Ecuaciones estándar de una parábola

La ecuación estándar de una parábola es,

y = hacha ² + bx + c

(o)

x = es ² + por + c

donde a nunca puede ser cero.

Partes de una parábola

Algunos términos y partes importantes de una parábola son:

• Enfocar: El foco es el punto fijo de una parábola.

• Directora: La directriz de una parábola es la recta perpendicular al eje de una parábola.

• Cuerda Focal: La cuerda que pasa por el foco de una parábola, cortando la parábola en dos puntos distintos, se llama cuerda focal.

• Distancia focal: La distancia focal es la distancia de un punto (x₁, y₁) en la parábola desde el foco.

• Lado derecho: Un latus recto es una cuerda focal que pasa por el foco de una parábola y es perpendicular al eje de la parábola. La longitud del lado recto es LL’ = 4a.

• Excentricidad: La relación entre la distancia de un punto al foco y su distancia a la directriz se llama excentricidad (e). Para una parábola, la excentricidad es igual a 1, es decir, e = 1.

Una parábola tiene cuatro ecuaciones estándar basadas en la orientación de la parábola y su eje. Cada parábola tiene un eje transversal y un eje conjugado diferente.

Ecuación de la parábola	Parábola	Fórmulas de parámetros de una parábola
y 2 = 4 ejes	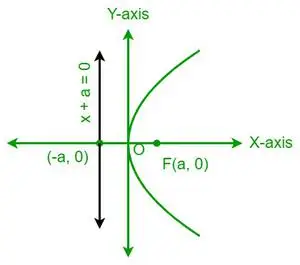Parábola horizontal	Vértice = (0,0) Enfoque = (a, 0) La parábola se abre hacia el lado derecho. La ecuación del eje es y = 0. La ecuación de la directriz es x + a = 0 Longitud del lado recto = 4a
y 2 = -4ax	Parábola horizontal	Vértice = (0,0) Enfoque = (-a, 0) La parábola se abre hacia el lado izquierdo. La ecuación del eje es y = 0. La ecuación de la directriz es x – a = 0 Longitud del lado recto = 4a
X 2 = 4 días	Parábola vertical	Vértice = (0,0) Enfoque = (0, a) La parábola se abre hacia arriba. La ecuación del eje es x = 0. La ecuación de la directriz es y + a = 0 Longitud del lado recto = 4a
X 2 = -4 días	Parábola vertical	Vértice = (0,0) Enfoque = (0, -a) La parábola se abre hacia abajo. La ecuación del eje es x = 0. La ecuación de la directriz es y – a = 0 Longitud del lado recto = 4a

Las siguientes son las observaciones realizadas a partir de la forma estándar de ecuaciones de una parábola:

• Una parábola es simétrica con respecto a su eje. Por ejemplo, y²= 4ax es simétrico con respecto al eje x, mientras que x²= 4ay es simétrico con respecto al eje y.

• Si una parábola es simétrica con respecto al eje x, entonces la parábola se abre hacia la derecha si el coeficiente x es positivo y hacia la izquierda si el coeficiente x es negativo.

• Si una parábola es simétrica con respecto al eje y, entonces la parábola se abre hacia arriba si el coeficiente y es positivo y hacia abajo si el coeficiente y es negativo.

Las siguientes son las ecuaciones estándar de una parábola cuando el eje de simetría es paralelo al eje x o al eje y y el vértice no está en el origen.

Ecuación de la parábola	Parábola	Fórmulas de parámetros de una parábola
(y – k)2= 4a(x-h)	Parábola horizontal	Vértice = (h, k) Enfoque = (h + a, k) La parábola se abre hacia el lado derecho. La ecuación del eje es y = k. La ecuación de la directriz es x = h – a Longitud del lado recto = 4a
(y – k)2= -4a(x-h)	Parábola horizontal	Vértice = (h, k) Enfoque = (h – a, k) La parábola se abre hacia el lado izquierdo. La ecuación del eje es y = k. La ecuación de la directriz es x = h + a Longitud del lado recto = 4a
(x-h)2= 4a(y – k)	Parábola vertical	Vértice = (h, k) Enfoque = (h, k + a) La parábola se abre hacia arriba. La ecuación del eje es x = h. La ecuación de la directriz es y = k – a Longitud del lado recto = 4a
(x-h)2= -4a(y – k)	Parábola vertical	Vértice = (h, k) Enfoque = (h, k – a) La parábola se abre hacia abajo. La ecuación del eje es x = h. La ecuación de la directriz es y = k + a Longitud del lado recto = 4a

Ecuación de derivación de parábola

Sea P un punto de la parábola cuyas coordenadas son (x, y). Según la definición de parábola, la distancia del punto P al foco (F) es igual a la distancia del mismo punto P a la directriz de una parábola. Ahora, consideremos un punto X en la directriz, cuyas coordenadas son (-a, y).

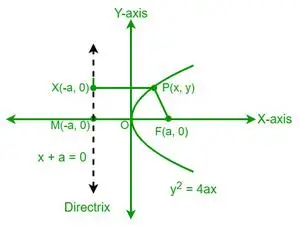
De la definición de excentricidad de una parábola, tenemos

mi = PF/PX = 1

⇒ PF = PX

Las coordenadas del foco son (a, 0). Ahora, usando la fórmula de distancia de coordenadas, podemos encontrar la distancia del punto P (x, y) al foco F (a, 0).

FP = √[(x – a)²+ (y – 0)²]

⇒ FP = √[(x – a)²+ y²] —————— (1)

La ecuación de la directriz es x + a = 0. Para encontrar la distancia de PX, usamos la fórmula de la distancia perpendicular.

PX = (x + a)/√[1²+ 0²]

⇒ PX = x +a —————— (2)

Ya sabemos que PF = PX. Entonces, iguale las ecuaciones (1) y (2).

√[(x – a)²+ y²] = (x + a)

Al elevar al cuadrado ambos lados obtenemos,

⇒ [(x – a)²+ y²] = (x + a)²

⇒x²+ un²– 2ax + y²=x²+ un²+ 2 hachas

⇒ y²– 2 ejes = 2 ejes

⇒ y²= 2ax + 2ax ⇒ y ² = 4 ejes

Por tanto, hemos derivado la ecuación de una parábola. De manera similar, podemos derivar las ecuaciones estándar de las otras tres parábolas.

• y²= -4ax
• X²= 4 días
• X²= -4 días

y ² = 4ax, y ² = -4ax, x ² = 4ay, y x ² = -4 días son las ecuaciones estándar de una parábola.

Artículos relacionados con la parábola:

• Ecuación del círculo
• Ecuación de elipse
• Ecuación de la hipérbola
• Aplicaciones de la parábola en la vida real

Ejemplos de ecuación de una parábola

Ejemplo 1: Encuentre la longitud del latus recto, el foco y el vértice, si la ecuación de la parábola es y ² = 12x.

Solución:

Dado,

La ecuación de la parábola es y.²= 12x

Comparando la ecuación dada con la forma estándar y²= 4 ejes

4a = 12

⇒ a = 12/4 = 3

Lo sabemos,

Lado derecho de una parábola = 4a = 4 (3) = 12

Ahora, foco de la parábola = (a, 0) = (3, 0)

Vértice de la parábola dada = (0, 0)

Ejemplo 2: Encuentre la ecuación de la parábola que es simétrica con respecto al eje X y pasa por el punto (-4, 5).

Solución:

Dado,

La parábola es simétrica con respecto al eje X y tiene su vértice en el origen.

Por tanto, la ecuación puede tener la forma y²= 4ax o y²= -4ax, donde el signo depende de si la parábola se abre hacia el lado izquierdo o hacia el lado derecho.

La parábola debe abrirse hacia la izquierda ya que pasa por (-4, 5) que se encuentra en el segundo cuadrante.

Entonces la ecuación será: y²= -4ax

Sustituyendo (-4, 5) en la ecuación anterior,

⇒ (5)²= -4a(-4)

⇒ 25 = 16a

⇒ a = 25/16

Por tanto, la ecuación de la parábola es: y²= -4(25/16)x (o) 4y²= -25x.

Ejemplo 3: Encuentre las coordenadas del foco, el eje, la ecuación de la directriz y el latus recto de la parábola x ² = 16 años.

Solución:

Dado,

La ecuación de la parábola es: x²= 16 años

Comparando la ecuación dada con la forma estándar x²= 4 días,

4a = 16 ⇒ a = 4

El coeficiente de y es positivo por lo que la parábola se abre hacia arriba.

Además, el eje de simetría está a lo largo del eje Y positivo.

Por eso,

El foco de la parábola es (a, 0) = (4, 0).

La ecuación de la directriz es y = -a, es decir, y = -4 o y + 4 = 0.

Longitud del lado recto = 4a = 4(4) = 16.

Ejemplo 4: Encuentre la longitud del latus recto, el foco y el vértice si la ecuación de una parábola es 2(x-2) ² + 16 = y.

Solución:

Dado,

La ecuación de una parábola es 2(x-2)²+ 16 = y

Comparando la ecuación dada con la ecuación general de una parábola y = a(x – h)²+k, obtenemos

un = 2

(h, k) = (2, 16)

Lo sabemos,

Longitud del latus recto de una parábola = 4a

= 4(2) = 8

Ahora, foco= (a, 0) = (2, 0)

Ahora, Vértice = (2, 16)

Ejemplo 5: La ecuación de una parábola es x ² – 12x + 4y – 24 = 0, luego encuentra su vértice, foco y directriz.

Solución:

Dado,

La ecuación de la parábola es x.²– 12x + 4y – 24 = 0

⇒x²– 12x + 36 – 36 + 4y – 24 = 0

⇒ (x – 6)²+ 4 años – 60 = 0

⇒ (x – 6)²= -4(y + 15)

La ecuación obtenida tiene la forma (x – h)²= -4a(y – k)

-4a = -4 ⇒ a = 1

Entonces, el vértice = (h, k) = (6, – 15)

Enfoque = (h, k – a) = (6, -15-1) = (6, -16)

La ecuación de la directriz es y = k + a

⇒ y = -15 + 1 ⇒ y = -14

⇒ y + 14 = 0

Preguntas frecuentes sobre la ecuación de la parábola

¿Cómo se encuentra la ecuación estándar de una parábola?

La forma estándar de parábola es y.²= 4ax o x²= 4 días.

¿Cuál es la ecuación normal de la parábola?

Ecuación de normal a la parábola y²= 4ax con pendiente m viene dado por: y = mx – 2am – am ³

¿Cómo se encuentra el vértice de una parábola?

Para una parábola dada: y = ax²+ bx + c su vértice se puede encontrar usando la fórmula x = − b/2a. Vuelve a introducir este valor de x en la ecuación para encontrar la coordenada y correspondiente.

estado de git -s