La ley de enfriamiento de Newton es la ley fundamental que describe la tasa de transferencia de calor de un cuerpo a su entorno a través de la radiación. Esta ley establece que la velocidad a la que un cuerpo irradia calor es directamente proporcional a la diferencia de temperatura del cuerpo con respecto a su entorno, dado que la diferencia de temperatura es baja. es decir, cuanto mayor es la diferencia entre la temperatura del cuerpo y su entorno, más calor se pierde y cuanto menor es la temperatura, menos calor se pierde. La ley de enfriamiento de Newton es un caso especial de la ley de Stefan-Boltzmann.

En este artículo, aprenderemos en detalle la ley de enfriamiento de Newton, la fórmula de la ley de enfriamiento de Newton, su derivación, ejemplos y otros.

Definición de la ley de enfriamiento de Newton

Newton Fue el primero en estudiar la relación entre el calor perdido por un cuerpo respecto a su entorno. Afirma que cuanto mayor es la diferencia de temperatura entre el objeto y su entorno, más calor irradia el cuerpo.

Ley de enfriamiento de Newton Establece que

La tasa de pérdida de calor de un cuerpo es directamente proporcional a la diferencia de temperatura entre el cuerpo y su entorno, dado que la diferencia de temperatura no es grande.

Esta ley se utiliza para explicar por qué el agua o la leche caliente que se deja en la mesa se enfría más rápido que un poco de leche o agua tibia que se deja en la mesa. La ley de enfriamiento de Newton nos ayuda a determinar la temperatura de cualquier persona sin tener que medirla, dada la temperatura inicial del cuerpo y la temperatura del entorno.

Fórmula de la ley de enfriamiento de Newton

La fórmula de la ley de enfriamiento de Newton es una fórmula para calcular la temperatura de un material a medida que pierde calor hacia su entorno a través de la radiación.

Según la ley de enfriamiento de Newton,

La tasa de pérdida de calor ( – dQ/dt) del cuerpo es directamente proporcional a la diferencia de temperatura [ΔT = (T ₂ –T ₁ )] del cuerpo y del entorno.

matriz dinámica java

Podemos representarlo como,

– dQ/dt ∝ (T ₂ –T ₁ )

– dQ/dt = k(T ₂ –T ₁ )

dónde,
k es una constante de proporcionalidad

Resolviendo la ecuación diferencial anterior obtenemos,

T(t) = T _s + (t _oh –T _s ) Es ^-kt

dónde,
t es la hora
T(t) es la temperatura del cuerpo en el momento t
t _s es la temperatura ambiente
t _oh es la temperatura inicial del cuerpo
k es la constante de proporcionalidad

Derivación de la ley de enfriamiento de Newton

La fórmula de la ley de enfriamiento de Newton se puede derivar utilizando la solución de la ecuación diferencial. Sea un cuerpo de masa m, con capacidad calorífica específica s, a temperatura T₂y T₁es la temperatura del entorno.

Si la temperatura baja un poco dT ₂ a tiempo dt , entonces la cantidad de calor perdido es,

dQ = msdT ₂

La tasa de pérdida de calor está dada por,

dQ/dt = ms (dT ₂ /dt)

Según la ley de enfriamiento de Newton,

– dQ/dt = k(T ₂ –T ₁ )

Comparando la ecuación anterior

– ms (dT ₂ /dt) = k (T ₂ –T ₁ )

dT ₂ /(t ₂ –T ₁ ) = – (k/ms) dt

dT ₂ /(t ₂ –T ₁ ) = – Kdt

método tostring en java

dónde, K = k/m·s

Integrando la ecuación anterior

registro _Es (t ₂ –T ₁ ) = – K t + c

t ₂ =T ₁ + C' y ^–kt

dónde, C' = mi ^C

La relación entre la caída de la temperatura del cuerpo y el tiempo se muestra mediante el gráfico de enfriamiento. La pendiente de este gráfico muestra la tasa de caída de la temperatura.

La curva de enfriamiento es un gráfico que muestra la relación entre la temperatura corporal y el tiempo. La tasa de caída de temperatura está determinada por la pendiente de la tangente a la curva en cualquier punto. La imagen agregada a continuación muestra la caída de temperatura y la relación de tiempo.

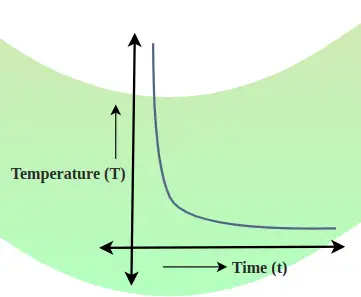
En general,

T(t) = T _A +(t _h -T _A )Es ^-kt

dónde
T(t) es la temperatura en el momento t
t _A es la temperatura ambiente o temperatura del entorno
t _h es la temperatura del objeto caliente
k es la constante positiva y t es el tiempo

Métodos para aplicar la ley de enfriamiento de Newton

A una velocidad de enfriamiento constante, la velocidad de enfriamiento está relacionada con la temperatura promedio del cuerpo durante el intervalo, luego podemos calcular el valor aproximado, usando la Ley de Enfriamiento de Newton.

dθ/dt = k(q – q _s )

dónde,
q es la temperatura del cuerpo
q _s es la temperatura del entorno

Ahora bien, si la temperatura promedio del cuerpo es q, donde,

q = (q _i +q _F )/2

Verificación de la ley de enfriamiento de Newton

Podemos verificar fácilmente la ley de enfriamiento de Newton mediante el experimento que se describe a continuación:

En el experimento tomamos un recipiente de doble pared (V) con agua entre las dos paredes. Dentro del recipiente de doble pared, colocamos un calorímetro de cobre (C) que contiene agua caliente.

Usamos dos termómetros T₂medir las temperaturas del agua en el calorímetro y T₁para medir la temperatura del agua caliente entre las paredes dobles. Después de intervalos de tiempo iguales, se anotan ambas temperaturas y se dibuja una gráfica entre el registro_Es(t₂–T₁) y se traza el tiempo (t) que aparece como una línea recta con pendiente negativa.

Gráfico de la ley de enfriamiento de Newton

A continuación se agrega la gráfica de la Ley de Enfriamiento de Newton, en esta gráfica se muestra el registro de diferencia entre las dos temperaturas y el tiempo.

Limitaciones de la ley de enfriamiento de Newton

Varias limitaciones de la ley de enfriamiento de Newton son,

• La ley de enfriamiento de Newton es válida si la diferencia de temperatura entre el cuerpo y el medio ambiente es pequeña.
• La pérdida de calor por el cuerpo es sólo en forma de Radiación .
• La temperatura del entorno debe permanecer constante durante el enfriamiento del cuerpo; de lo contrario, la ley de enfriamiento de Newton no se cumple.

Aplicaciones de la ley de enfriamiento de Newton

Varias aplicaciones de la ley de enfriamiento de Newton son,

• Estimar cuánto tiempo tardará un objeto caliente en enfriarse hasta una temperatura específica.
• Determinar la temperatura de una bebida en un refrigerador después de que haya transcurrido un período de tiempo determinado.
• Ayuda a indicar la hora de la muerte observando la posible temperatura corporal en el momento de la muerte y la temperatura corporal actual.

Leer más,

• Capacidad calorífica específica
• Concepto básico de termodinámica
• Procesos termodinámicos

Ejemplos resueltos Ley de enfriamiento de Newton

Ejemplo 1: Una sartén llena de comida caliente se enfría de 94 °C a 86 °C en 2 minutos cuando la temperatura ambiente es de 20 °C. ¿Cuánto tiempo tardará en enfriarse de 71 °C a 69 °C?

Solución:

El promedio de 94 °C y 86 °C es 90 °C,

• t₂= 90ºC
• t₁= 20ºC

Caída en tem. de alimento es de 8°C en 2 minutos.

Según la ley de enfriamiento de Newton,

– dQ/dt = k(T ₂ –T ₁ )

8 °C/2 min = k(90 – 20)

4 = k(70) ………(1)

El promedio de 69 °C y 71 °C es 70 °C

mejor hentai

• t₂= 70ºC
• t₁= 20ºC

Según la ley de enfriamiento de Newton,

2°C/dt = k(70 – 20) ……(2)

De la ecuación (1) y (2),

Cambio en el tiempo = 0,7 min = =42 seg

Por lo tanto, la comida tardará 42 segundos en enfriarse de 71 °C a 69 °C.

Ejemplo 2: Un cuerpo a una temperatura de 40ºC se mantiene en un entorno a temperatura constante de 20ºC. Se observa que su temperatura baja a 35ºC en 10 minutos. Calcula cuánto tiempo más le tomará al cuerpo alcanzar una temperatura de 30ºC.

Solución:

Dado,

• q_i= (40 – 20)ºC
• q_F= (35 – 20)ºC

Según la ley de enfriamiento de Newton

q _F =q _i Es ^-kt

Ahora, para el intervalo en el que la temperatura baja de 40 ºC a 35 ºC.

(35 – 20) = (40 – 20) y^-(10k)

Es^-10k= 3/4

-10k = (en 4/3)

k = 0,2876/10

k = 0,02876

Ahora usando nuevamente la Fórmula de Newton,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

Es^-kt= 2/3

-kt = ln(2/3)

t = 0,40546/k

Usando el valor de k,

t = 0,40546/0,02876

que significa xdxd

t = 14.098 min

Así, el tiempo que tarda el cuerpo en alcanzar la temperatura de 30ºC es de 14.098 min.

Ejemplo 3: Se calienta el aceite a 70 ºC. Se enfría a 50 ºC al cabo de 6 minutos. Calcule el tiempo que tarda el aceite en enfriarse de 50 ºC a 40 ºC dada la temperatura ambiente T _s = 25ºC

Solución:

Dado,

La temperatura del aceite después de 6 min, es decir, T(t) es igual a 50 ºC

• Temperatura ambiente T_s= 25ºC
• Temperatura del aceite, T_oh= 70ºC
• Tiempo para enfriar a 50ºC = 6 min

Según la ley de enfriamiento de Newton,

T(t) = T_s+ (t₀–T_s) Es^-kt

{T(t) – T_s}/(T_oh–T_s) = y^-kt

-kt = ln[(T(t) – T_s)/(T_oh–T_s)] ………(1)

Sustituir los valores

-kt = ln[(50 – 25)/(70 – 25)]

-k = (en 0,55556)/6

k = 0,09796

Temperatura promedio de 50 ºC a 40 ºC es igual a 45 ºC

Nuevamente usando la ley de enfriamiento de Newton

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8.278 minutos

Así, el tiempo que tarda el aceite en enfriarse de 50 ºC a 40 ºC es 8.278 minutos

Ejemplo 4: Se calienta agua a 80 ºC durante 10 min. ¿Cuál sería su temperatura en grados Celsius, si k = 0,056 por min y la temperatura circundante es de 25 ºC?

Solución:

Dado,

• Temperatura ambiente T_s= 25ºC
• Temperatura del agua T₀= 80ºC
• Tiempo durante el cual se calienta el agua (t) = 10 min
• Valor de la constante k = 0,056.

Según la ley de enfriamiento de Newton,

T(t) = T_s+ (t₀–T_s) Es^-kt

Sustituyendo el valor

T(t)= 25 + (80 – 25)e^-(0.056×10)

T(t) = 25 + 55 mi^-(0.056×10)

T(t) = 25 + 31,42

T(t) = 56,42

cadena.formato java cadena

Después de 10 min la temperatura del agua sería 56,42 ºC.

Preguntas frecuentes sobre la ley de enfriamiento de Newton

P1: ¿Qué es la ley de enfriamiento de Newton?

Respuesta:

La ley de enfriamiento de Newton establece que la tasa de pérdida de calor de un cuerpo es directamente proporcional a la diferencia de temperatura entre el cuerpo y su entorno.

P2: ¿Cuál es la fórmula de la ley de enfriamiento de Newton?

Respuesta:

La fórmula de la ley de enfriamiento de Newton establece que,

T(t) = T _s + (t _oh –T _s ) Es ^-kt

P3: ¿Qué es k en la ley de enfriamiento de Newton?

Respuesta:

El k en la fórmula de la Ley de Enfriamiento de Newton es la constante que depende del material, es decir, cambiar el material cambia el k en la ley de enfriamiento de Newton.

P4: ¿Por qué la leche caliente es más fácil de beber en un bol que en un vaso?

Respuesta:

El cuenco tiene una superficie mayor que el vidrio, por lo que se pierde más calor hacia su entorno en forma de radiación de calor a través del cuenco y, por lo tanto, nos resulta más fácil beber leche caliente del cuenco.