• El algoritmo Naïve Bayes es un algoritmo de aprendizaje supervisado, que se basa en Teorema de Bayes y se utiliza para resolver problemas de clasificación.
• Se utiliza principalmente en clasificación de texto que incluye un conjunto de datos de entrenamiento de alta dimensión.
• Naïve Bayes Classifier es uno de los algoritmos de clasificación más simples y efectivos que ayuda a construir modelos rápidos de aprendizaje automático que pueden realizar predicciones rápidas.
Es un clasificador probabilístico, lo que significa que predice en función de la probabilidad de un objeto..
• Algunos ejemplos populares de algoritmo Naïve Bayes son Filtración de spam, análisis sentimental y clasificación de artículos. .

¿Por qué se llama Naïve Bayes?

El algoritmo Naïve Bayes se compone de dos palabras Naïve y Bayes, que pueden describirse como:

Ingenuo: Se llama ingenuo porque supone que la aparición de una determinada característica es independiente de la aparición de otras características. Por ejemplo, si la fruta se identifica según el color, la forma y el sabor, entonces la fruta roja, esférica y dulce se reconoce como una manzana. De ahí que cada rasgo contribuya individualmente a identificar que es una manzana sin depender unos de otros.Bayes: Se llama Bayes porque depende del principio del Teorema de Bayes.

Teorema de Bayes:

• El teorema de Bayes también se conoce como Regla de Bayes o ley de bayes , que se utiliza para determinar la probabilidad de una hipótesis con conocimiento previo. Depende de la probabilidad condicional.
• La fórmula del teorema de Bayes viene dada por:

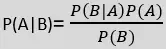
Dónde,

P(A|B) es probabilidad posterior : Probabilidad de la hipótesis A sobre el evento observado B.

P (B | A) es probabilidad de probabilidad : Probabilidad de la evidencia dado que la probabilidad de una hipótesis es verdadera.

P(A) es probabilidad previa : Probabilidad de la hipótesis antes de observar la evidencia.

P(B) es probabilidad marginal : Probabilidad de evidencia.

Funcionamiento del clasificador Naïve Bayes:

El funcionamiento del clasificador Naïve Bayes se puede entender con la ayuda del siguiente ejemplo:

Supongamos que tenemos un conjunto de datos de las condiciones climáticas y la variable objetivo correspondiente ' Jugar '. Entonces, utilizando este conjunto de datos, debemos decidir si debemos jugar o no en un día en particular según las condiciones climáticas. Entonces, para resolver este problema, debemos seguir los pasos a continuación:

1. Convierta el conjunto de datos dado en tablas de frecuencia.
2. Genere una tabla de probabilidad encontrando las probabilidades de características determinadas.
3. Ahora, use el teorema de Bayes para calcular la probabilidad posterior.

Problema : Si hace sol, ¿el jugador debería jugar o no?

conversión de cadena a int en java

Solución : Para resolver esto, primero considere el siguiente conjunto de datos:

Tabla de frecuencia de las condiciones climáticas:

Tabla de probabilidad de condiciones climáticas:

Aplicando el teorema de Bayes:

P(Sí|Soleado)= P(Soleado|Sí)*P(Sí)/P(Soleado)

P(Soleado|Sí)= 3/10= 0,3

P(soleado)= 0,35

P(Sí)=0,71

par c ++

Entonces P(Sí|Soleado) = 0,3*0,71/0,35= 0.60

P(No|Soleado)= P(Soleado|No)*P(No)/P(Soleado)

P(soleado|NO)= 2/4=0.5

P(No)= 0.29

P(soleado)= 0,35

Entonces P(No|Soleado)= 0.5*0.29/0.35 = 0.41

Como podemos ver en el cálculo anterior que P(Sí|Soleado)>P(No|Soleado)

Por lo tanto, en un día soleado, el jugador puede jugar.

xd xd significado

Ventajas del clasificador Naïve Bayes:

• Naïve Bayes es uno de los algoritmos de aprendizaje automático rápidos y sencillos para predecir una clase de conjuntos de datos.
• Se puede utilizar tanto para clasificaciones binarias como multiclase.
• Funciona bien en predicciones de clases múltiples en comparación con otros algoritmos.
• Es la opción más popular para problemas de clasificación de textos .

Desventajas del clasificador Naïve Bayes:

• Naive Bayes supone que todas las características son independientes o no están relacionadas, por lo que no puede aprender la relación entre las características.

Aplicaciones del clasificador Naïve Bayes:

• Se utiliza para Puntuacion de credito .
• Se utiliza en clasificación de datos médicos .
• Se puede utilizar en predicciones en tiempo real porque Naïve Bayes Classifier aprende con entusiasmo.
• Se utiliza en la clasificación de texto, como Filtrado de spam y Análisis de los sentimientos .

Tipos de modelo Naïve Bayes:

Hay tres tipos de modelo Naive Bayes, que se detallan a continuación:

gaussiano: El modelo gaussiano supone que las características siguen una distribución normal. Esto significa que si los predictores toman valores continuos en lugar de discretos, entonces el modelo supone que estos valores se muestrean a partir de la distribución gaussiana.multinomial: El clasificador Multinomial Naïve Bayes se utiliza cuando los datos tienen una distribución multinomial. Se utiliza principalmente para problemas de clasificación de documentos, lo que significa que un documento en particular pertenece a qué categoría, como deportes, política, educación, etc.
El clasificador utiliza la frecuencia de las palabras para los predictores.bernoulli: El clasificador de Bernoulli funciona de manera similar al clasificador multinomial, pero las variables predictoras son las variables booleanas independientes. Por ejemplo, si una palabra en particular está presente o no en un documento. Este modelo también es famoso por tareas de clasificación de documentos.

Implementación en Python del algoritmo Naïve Bayes:

Ahora implementaremos un algoritmo Naive Bayes usando Python. Entonces, para esto usaremos el ' datos del usuario ' conjunto de datos , que hemos utilizado en nuestro otro modelo de clasificación. Por lo tanto, podemos comparar fácilmente el modelo Naive Bayes con los otros modelos.

Pasos para implementar:

• Paso de preprocesamiento de datos
• Adaptación de Naive Bayes al conjunto de entrenamiento
• Predecir el resultado de la prueba
• Pruebe la precisión del resultado (Creación de matriz de confusión)
• Visualizando el resultado del conjunto de pruebas.

1) Paso de preprocesamiento de datos:

En este paso, procesaremos/prepararemos previamente los datos para que podamos usarlos de manera eficiente en nuestro código. Es similar a lo que hicimos en el preprocesamiento de datos. El código para esto se proporciona a continuación:

 Importing the libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd # Importing the dataset dataset = pd.read_csv('user_data.csv') x = dataset.iloc[:, [2, 3]].values y = dataset.iloc[:, 4].values # Splitting the dataset into the Training set and Test set from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 0) # Feature Scaling from sklearn.preprocessing import StandardScaler sc = StandardScaler() x_train = sc.fit_transform(x_train) x_test = sc.transform(x_test) 

En el código anterior, hemos cargado el conjunto de datos en nuestro programa usando ' conjunto de datos = pd.read_csv('user_data.csv') . El conjunto de datos cargado se divide en conjunto de entrenamiento y de prueba, y luego escalamos la variable de característica.

El resultado del conjunto de datos se proporciona como:

2) Adaptación de Naive Bayes al conjunto de entrenamiento:

Después del paso de preprocesamiento, ahora ajustaremos el modelo Naive Bayes al conjunto de entrenamiento. A continuación se muestra el código para ello:

 # Fitting Naive Bayes to the Training set from sklearn.naive_bayes import GaussianNB classifier = GaussianNB() classifier.fit(x_train, y_train) 

En el código anterior, hemos utilizado el clasificador gaussiano NB para ajustarlo al conjunto de datos de entrenamiento. También podemos utilizar otros clasificadores según nuestros requisitos.

Producción:

 Out[6]: GaussianNB(priors=None, var_smoothing=1e-09) 

3) Predicción del resultado del conjunto de pruebas:

Ahora predeciremos el resultado del conjunto de pruebas. Para esto, crearemos una nueva variable predictiva. y_pred y utilizará la función de predicción para hacer las predicciones.

 # Predicting the Test set results y_pred = classifier.predict(x_test) 

Producción:

El resultado anterior muestra el resultado del vector de predicción. y_pred y vector real y_test. Podemos ver que algunas predicciones son diferentes de los valores reales, que son predicciones incorrectas.

precedencia del operador java

4) Crear matriz de confusión:

Ahora comprobaremos la precisión del clasificador Naive Bayes utilizando la matriz de confusión. A continuación se muestra el código para ello:

 # Making the Confusion Matrix from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred) 

Producción:

Como podemos ver en el resultado de la matriz de confusión anterior, hay 7+3= 10 predicciones incorrectas y 65+25=90 predicciones correctas.

5) Visualizar el resultado del conjunto de entrenamiento:

A continuación visualizaremos el resultado del conjunto de entrenamiento utilizando el Clasificador Na�ve Bayes. A continuación se muestra el código para ello:

 # Visualising the Training set results from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Producción:

En el resultado anterior podemos ver que el clasificador Na�ve Bayes ha segregado los puntos de datos con el límite fino. Es la curva gaussiana como hemos usado. GaussianoNB clasificador en nuestro código.

6) Visualización del resultado del conjunto de pruebas:

 # Visualising the Test set results from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Producción:

El resultado anterior es el resultado final para los datos del conjunto de prueba. Como podemos ver, el clasificador ha creado una curva gaussiana para dividir las variables 'compradas' y 'no compradas'. Hay algunas predicciones erróneas que hemos calculado en la matriz de confusión. Pero aún así es un clasificador bastante bueno.