El momento de inercia es propiedad de un cuerpo en movimiento de rotación. El momento de inercia es la propiedad de los cuerpos en rotación que tiende a oponerse al cambio en el movimiento de rotación del cuerpo. Es similar a la inercia de cualquier cuerpo en movimiento de traslación. Matemáticamente, el Momento de Inercia viene dado como la suma del producto de la masa de cada partícula y el cuadrado de la distancia al eje de rotación. Se mide en la unidad de kgm 2 .
Aprendamos sobre el momento de inercia en detalle en el artículo siguiente.
Tabla de contenidos
- Definición de momento de inercia
- Fórmula del momento de inercia
- Factores que afectan el momento de inercia
- ¿Cómo calcular el momento de inercia?
- Fórmula del momento de inercia para diferentes formas
- Radio de giro
- Teoremas del momento de inercia
- Momentos de inercia para diferentes objetos
Definición de momento de inercia
El momento de inercia es la tendencia de un cuerpo en movimiento de rotación que se opone al cambio en su movimiento rotacional debido a fuerzas externas. El Momento de Inercia se comporta como una masa angular y se llama inercia rotacional. El momento de inercia es análogo al mecánico. Inercia del cuerpo.
MOI se define como la cantidad expresada por la suma del producto de las masa de cada partícula con el cuadrado de su distancia al eje de rotación para cualquier partícula que realice el movimiento de rotación.
Unidad de momento de inercia
El momento de inercia es una cantidad escalar y la unidad SI del momento de inercia es kgm 2 .
Fórmula dimensional del momento de inercia
Dado que el Momento de Inercia se da como el producto de la masa por el cuadrado de la distancia. Es fórmula dimensional viene dado por el producto de la fórmula dimensional de masa y el cuadrado de la fórmula dimensional de longitud. La fórmula dimensional del momento de inercia es, ml 2
¿Qué es la inercia?
La inercia es la propiedad de una materia en virtud de la cual tiende a resistir el cambio de estado de su movimiento. Esto significa que un cuerpo en reposo intenta permanecer en reposo y resistir cualquier fuerza que intente ponerlo en movimiento, y un cuerpo en movimiento intenta continuar en movimiento y resistir cualquier fuerza que intente ponerlo en movimiento para cambiar la magnitud de su movimiento. En términos de cantidad, es igual a la fuerza máxima que intenta cambiar su estado de movimiento .
Aprender más acerca de Inercia .
Fórmula del momento de inercia
El momento de inercia es un cantidad escalar . Matemáticamente, el producto del cuadrado de la masa de una partícula por la distancia al eje de rotación se llama momento de inercia de la partícula con respecto al eje de rotación.
La fórmula general para encontrar el momento de inercia de cualquier objeto es,
yo = señor 2
dónde,
metro es la masa del objeto'
r es la distancia desde el eje de rotación
Para un cuerpo formado por partículas continuas infinitamente pequeñas, la forma integral del momento de inercia se utiliza para calcular el momento de inercia.
yo = ∫dyo
yo =
int_{0}^{M} r^2 dm
Momento de inercia de un sistema de partículas
El momento de inercia de un sistema de partículas viene dado por la fórmula,
yo = ∑metro i r i 2
dónde,
r i es la distancia perpendicular de la ithpartícula del eje
metro i es la masa de ithpartícula
La ecuación del momento de inercia anterior indica que el momento de inercia de un sistema de partículas es igual a la suma del producto de la masa de cada una y el cuadrado de la distancia desde el eje de rotación de cada partícula.
Para la figura que se muestra a continuación,
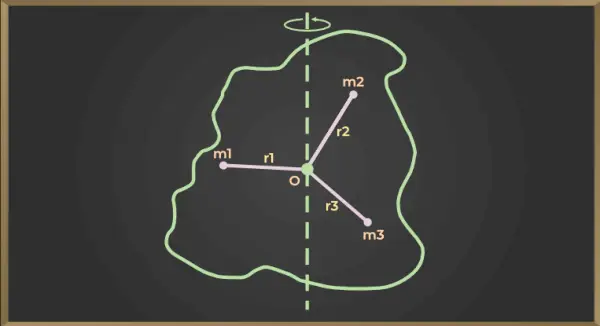
Momento de inercia de la primera partícula = m1×r12
Momento de inercia de la segunda partícula = m2×r22
Momento de inercia de la tercera partícula = m3×r32
Similarmente,
Momento de inercia de nthpartícula = mnorte×rnorte2
Ahora el momento de inercia de todo el cuerpo respecto del eje de rotación. AB será igual a la suma del momento de inercia de todas las partículas, por lo que
yo = m1×r12+m2×r22+m3×r32+……+mnorte×rnorte2
corte
yo = Σm i ×r i 2
dónde,
I Representa el momento de inercia del cuerpo respecto del eje de rotación.
metro i es la masa de ithpartícula,
r i es el radio de ithpartícula
S representa la suma.
De la ecuación, podemos decir que el momento de inercia de un cuerpo alrededor de un eje fijo es igual a la suma del producto de la masa de cada partícula de ese cuerpo por el cuadrado de su distancia perpendicular al eje fijo.
Factores que afectan el momento de inercia
El momento de inercia de cualquier objeto depende de los siguientes valores:
- Forma y tamaño del objeto.
- Densidad del material del objeto.
- Eje de rotación
¿Cómo calcular el momento de inercia?
Se utilizan varias formas para calcular el momento de inercia de cualquier objeto en rotación.
- Para objetos uniformes, el momento de inercia se calcula tomando el producto de su masa por el cuadrado de su distancia al eje de rotación (r2).
- Para objetos no uniformes, calculamos el momento de inercia tomando la suma del producto de las masas puntuales individuales en cada radio diferente, para esto la fórmula utilizada es
yo = ∑metro i r i 2
Fórmula del momento de inercia para diferentes formas
Esta tabla analiza expresiones para el momento de inercia de algunos objetos simétricos junto con su eje de rotación:

| Objeto | Eje | Expresión del momento de inercia |
|---|---|---|
| Cilindro hueco de pared delgada | Central | yo = señor2 |
| Anillo fino | Diámetro | yo = 1/2 señor2 |
| Anillo anular o cilindro hueco | Central | Yo = 1/2 M(r22+r12) |
| Cilindro sólido | Central | yo = 1/2 señor2 |
| Disco uniforme | Diámetro | yo = 1/4 señor2 |
| Esfera hueca | Central | yo = 2/3 señor2 |
| Esfera sólida | Central | yo = 2/5 señor2 |
| Concha esférica simétrica uniforme | Central | |
| Placa Uniforme o Paralelepípedo Rectangular | Central | Yo = 1/12 M(a2+b2) |
| varilla delgada | Central | I = 1/12 Sr.2 |
| varilla delgada | Al final de la vara | yo = 1/3 señor2 |
Radio de giro
El Radio de giro de un cuerpo se define como la distancia perpendicular desde el eje de rotación hasta el punto de masa cuya masa es igual a la masa de todo el cuerpo y el Momento de Inercia es igual al momento de inercia real del objeto tal como ha sido Se supone que la masa total del cuerpo se concentra allí. Es una distancia imaginaria. El radio de giro se denota por K.
Si la masa y el radio de giro del cuerpo son M y K respectivamente, entonces el momento de inercia de un cuerpo es
yo = mk 2 ……(1)
Así, el radio de giro de un cuerpo es perpendicular al eje de rotación cuyo cuadrado multiplicado por la masa de ese cuerpo da el momento de inercia de ese cuerpo alrededor de ese eje.
Nuevamente por la ecuación (1), K2= yo/m
K = √(I/m)
Por tanto, el radio de giro de un cuerpo alrededor de un eje es igual a la raíz cuadrada de la relación del cuerpo alrededor de ese eje.
Teoremas del momento de inercia
Existen dos tipos de teoremas que son muy importantes con respecto al Momento de Inercia:
idea intellij vs eclipse
- Teorema de los ejes paralelos
- Teorema del eje perpendicular
Teorema del eje perpendicular
Teorema del eje perpendicular establece que la suma del momento de inercia de un cuerpo alrededor de dos ejes mutuamente perpendiculares situados en el plano de un cuerpo es igual al momento de inercia del cuerpo alrededor del tercer eje que es perpendicular a los dos ejes y pasa por su punto de intersección.

En la figura anterior, BUEY y LIMITADO Hay dos ejes en el plano del cuerpo que son perpendiculares entre sí. El tercer eje es ONZ que es perpendicular al plano del cuerpo y pasa por el punto de intersección de los BUEY y LIMITADO ejes. Si I X , I y , y I Con son los momentos de inercia del cuerpo respecto del eje BUEY , LIMITADO , y ONZ ejes respectivamente, entonces de acuerdo con este teorema
I X + yo y = yo Con
Teorema de los ejes paralelos
De acuerdo a Teorema de los ejes paralelos , el momento de inercia de un cuerpo alrededor de un eje dado es la suma del momento de inercia alrededor de un eje que pasa por el centro de masa de ese cuerpo y el producto del cuadrado de la masa del cuerpo por la distancia perpendicular entre los dos ejes.

En la figura anterior, tenemos que encontrar el momento de inercia de I oh del cuerpo que pasa por el punto oh y alrededor del eje perpendicular al plano, mientras que el momento de inercia del cuerpo que pasa por el centro de masa C y alrededor de un eje paralelo al eje dado es I C , entonces según este teorema
I oh = yo C +ml 2
dónde
METRO es la masa de todo el cuerpo
yo es la distancia perpendicular entre dos ejes.
Momentos de inercia para diferentes objetos
El momento de inercia de diferentes objetos se analiza a continuación en este artículo.
Momento de inercia de una placa rectangular
Si la masa de la placa es M, longitud l y ancho b, entonces el momento de inercia pasa por el centro de gravedad y alrededor de un eje perpendicular al plano de la placa.

yo = M(l 2 +b 2 / 12)
Momento de inercia de un disco
Si el disco tiene una masa M y un radio r, entonces el momento de inercia alrededor del eje geométrico del disco es

Yo = 1/2(Sr. 2 )
Momento de inercia de una varilla
Si la masa de la varilla es M y la longitud es l, entonces el momento de inercia alrededor del eje perpendicular a la longitud de la varilla y que pasa por su centro de gravedad.

yo = ml 2 /12
Momento de inercia de un círculo
Si la masa del anillo es M y el radio del anillo es r, entonces el momento de inercia alrededor del eje que pasa perpendicularmente al centro del anillo es

yo = señor 2
Momento de inercia de una esfera
Si una esfera sólida tiene una masa de M y un radio de r, entonces el momento de inercia con respecto a su diámetro es

I = 2/5Sr. 2
Momento de inercia del cilindro sólido
El momento de inercia de un cilindro sólido de radio 'R' y masa M viene dado por

Yo = 1/2MR 2
Momento de inercia del cilindro hueco
Un cilindro hueco tiene dos radios, a saber, radio interno y radio externo. El momento de inercia de un cilindro hueco con masa M y radio externo R1, y radio interno R2se da como

Yo = 1/2M(R 1 2 +R 2 2 )
Momento de inercia de una esfera sólida
El momento de inercia de una esfera sólida de masa 'M' y radio 'R' se da como

Yo = 2/5MR 2
Momento de inercia de la esfera hueca
El momento de inercia de una esfera hueca de masa M y radio 'R' se da como

I = 2/3MR 2
Momento de inercia del anillo
El momento de inercia de un anillo está dado para dos casos en los que el eje de rotación pasa por el centro y cuando el eje de rotación pasa por el diámetro.
El momento de inercia del anillo con respecto al eje que pasa por el centro está dado por
convertir cadena a int

yo = señor 2
El momento de inercia del anillo con respecto al eje que pasa por el diámetro está dado por

yo = señor 2 /2
Momento de inercia del cuadrado
El momento de inercia del cuadrado del lado 'a' viene dado como

yo = un 4 /12
El momento de inercia de una placa cuadrada del lado de longitud 'l' y masa M viene dado como
Yo = 1/6ML 2
Momento de inercia del triángulo
El momento de inercia de un triángulo se da para 3 situaciones, primero, cuando el eje pasa por el centro, segundo cuando el eje pasa por la base y tercero cuando el eje es perpendicular a la base. Veamos la fórmula para ellos uno por uno. Para un triángulo de base 'b' y altura 'h', la fórmula para el momento de inercia se da de la siguiente manera

Cuando el eje pasa por el centroide
yo = bh 3 /36
Cuando el eje pasa por la base.
yo = bh 3 /12
Cuando el eje es perpendicular a la base.
Yo = (hb/36)(b 2 - b 1 b+b 1 2 )
Diferencia entre momento de inercia e inercia
La diferencia entre inercia y momento de inercia se tabula a continuación:
| S.No. | Inercia | Momento de inercia |
|---|---|---|
| 1. | Su importancia está en el movimiento lineal. | Su importancia está en el movimiento de rotación. |
| 2. | Es aquella propiedad de un objeto que se opone al cambio de estado del objeto en movimiento lineal. | El momento de inercia es aquella propiedad de un objeto que se opone al cambio de estado del objeto en movimiento de rotación. |
| 3. | La inercia de un objeto depende únicamente de su masa. | El momento de inercia de un objeto depende de su masa y de su distribución de masa con respecto al eje de rotación. |
| 4. | La inercia de un objeto es fija. | El momento de inercia de un objeto varía con respecto a diferentes ejes de rotación. |
Energía cinética del cuerpo giratorio.
Supongamos un cuerpo de masa 'm' que gira con velocidad v a una distancia 'r' del eje de rotación. Su velocidad angular entonces viene dada por ω = v/r entonces v = rω. Ahora sabemos que el Energía cinética de un cuerpo está dada por
KE = 1/2 mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2Vaya2
⇒ KE = 1/2Iω 2
Por tanto, la energía cinética de un cuerpo en rotación viene dada por la mitad del producto del momento de inercia y el velocidad angular del cuerpo. La energía cinética de un cuerpo en rotación también se llama Energía cinética rotacional . La fórmula de la energía cinética rotacional se da como
KE = 1/2Iω 2
El Momento de Inercia(I) es independiente de la velocidad angular del cuerpo. Es función de la masa del cuerpo en rotación y de la distancia del cuerpo al eje de rotación. Por lo tanto, observamos que el movimiento angular es análogo al movimiento lineal, esto significa que la importancia del momento de inercia es que da una idea de cómo se distribuyen las masas a diferentes distancias del eje de rotación en un cuerpo giratorio.
Aplicación del momento de inercia
El momento de inercia tiene varias aplicaciones, algunas de las cuales se analizan a continuación:
- Debido al mayor momento de inercia, la Tierra gira sobre su eje con la misma velocidad angular.
- Debajo del motor de juego infantil se encuentra una pequeña rueda móvil. Después de frotar esta rueda con el suelo y salir del motor, debido al momento de inercia de la rueda, el motor sigue funcionando durante un tiempo.
- Cada motor consta de una rueda grande y pesada unida a su eje, con la mayor parte de su masa en su circunferencia. Por tanto, su momento de inercia es alto. Esta rueda se llama volante. El par que impulsa el eje del motor sigue aumentando. Por lo tanto, la rotación del eje puede no ser uniforme, pero debido a la presencia de una rueda móvil con más inercia, el eje continúa girando a una velocidad casi uniforme.
- En la rueda de carros de bueyes, rickshaws, scooters, bicicletas, etc., la mayor parte de la masa se concentra en su círculo o borde. este aro o rutina está sujeto al eje de la rueda mediante radios rígidos. Al hacer esto aumenta su momento de inercia. Por lo tanto, cuando las piernas dejan de moverse mientras se anda en bicicleta, la rueda continúa girando durante algún tiempo.
Además, consulte
- Cinemática del movimiento rotacional
- Movimiento de un cuerpo rígido
- Movimiento rodante
Ejemplos resueltos sobre momentos de inercia
Ejemplo 1: Un cuerpo de 500 g de masa gira alrededor de un eje. la distancia del centro de masa del cuerpo al eje de rotación es de 1,2 m. Encuentre el momento de inercia del cuerpo con respecto al eje de rotación.
Solución:
Dado que M = 500 g = 0,5 kg, r = 1,2 m.
Obviamente, se puede suponer que toda la masa de un cuerpo está situada en su centro de masa. Luego el momento de inercia del cuerpo con respecto al eje de rotación.
yo = señor2
Yo = 0,5 × (1,2)2
Yo = 0,72 kg·m2
Ejemplo 2: El radio de revolución alrededor de un eje a 12 cm del centro de masa de un cuerpo de 1,2 kg de masa es 13 cm. Calcula el Radio de revolución y momento de inercia alrededor de un eje que pasa por el centro de masa.
Solución:
Teniendo en cuenta que M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, yoCM= ?
Del teorema del eje paralelo I = ICM+ml2
k2=KCM2+ yo2
o kCM2=K2– yo2
kCM2 = (13)2– (12)2= 25
kCM= 5
Ahora, Momento de Inercia ICM= MKCM2
ICM= 1.0 × (0.05)2= 2.5 × 10-3kg·m2
Ejemplo 3: Un cuerpo de 0,1 kg de masa gira alrededor de un eje. Si la distancia entre el centro de masa del cuerpo y el eje de rotación es de 0,5 m, entonces encuentre el momento de inercia del cuerpo.
Solución:
Teniendo en cuenta que M = 0,1 kg y r = 0,5 m
entonces yo = señor2
mostrar aplicaciones ocultasYo = 0,1 × (0,5)2
I = 0,025 kg·m2
Ejemplo 4: El momento de inercia de los anillos respecto de un eje que pasa por su centro perpendicular al plano del anillo circular es de 200 gm cm 2 . ¿Cuál será el momento de inercia con respecto a su diámetro?
Solución:
Momento de inercia de un anillo circular respecto de un eje que pasa por otro centro perpendicular a su plano.
SEÑOR2= 200 gramos cm2
Momento de inercia aproximado al diámetro.
= 1/2 señor2
= 1/2 × 200 = 100 gramos cm2
Preguntas frecuentes sobre momentos de inercia
¿Cómo calcular el Momento de Inercia?
La fórmula básica para encontrar el momento de inercia de cualquier objeto uniforme es,
yo = señor 2
dónde,
metro es la masa del objeto'
r es la distancia desde el eje de rotación
¿Cómo calcular el Momento de Inercia de una Viga?
El momento de inercia de una viga a lo largo del centro y el eje horizontal se calcula mediante la fórmula,
yo = ml 2 / 12
¿De qué depende el Momento de Inercia de un cuerpo?
El momento de inercia de cualquier objeto depende de los factores que se detallan a continuación:
- masa del cuerpo,
- Eje de rotación
- Forma y tamaño del objeto.
¿Cuál es la unidad de momento de inercia?
La unidad del momento de inercia es kgm 2
¿Puede el momento de inercia ser negativo?
No, el momento de inercia nunca puede ser negativo.
¿Qué es el momento de inercia de masa?
El momento de inercia de masa es la medida de la resistencia de un cuerpo al cambio en su momento angular o dirección. El momento de inercia de la masa para una masa puntual viene dado por I = mr2y para un sistema de partículas, el momento de inercia de la masa viene dado como I = Σimetroiri2
¿Qué es el momento de inercia del área?
El momento de inercia del área es propiedad de un plano de forma 2D que muestra cómo se dispersan los puntos con respecto a un eje arbitrario en un plano. El momento de inercia del área también se conoce como segundo momento de área o momento de área cuadrático. La fórmula para el momento de inercia del área en el plano xy se da como Ixy= ∫xy dxdxy = ∫xy dA
