En el mundo real aprendizaje automático En aplicaciones, es común tener muchas características relevantes, pero sólo un subconjunto de ellas puede ser observable. Cuando se trata de variables que a veces son observables y otras no, es posible utilizar los casos en los que esa variable es visible u observada para aprender y hacer predicciones para los casos en los que no es observable. Este enfoque a menudo se denomina manejo de datos faltantes. Al utilizar las instancias disponibles donde la variable es observable, los algoritmos de aprendizaje automático pueden aprender patrones y relaciones a partir de los datos observados. Estos patrones aprendidos se pueden utilizar para predecir los valores de la variable en los casos en que falta o no es observable.
El algoritmo de maximización de expectativas se puede utilizar para manejar situaciones en las que las variables son parcialmente observables. Cuando ciertas variables son observables, podemos usar esas instancias para aprender y estimar sus valores. Luego, podemos predecir los valores de estas variables en los casos en que no sea observable.
El algoritmo EM fue propuesto y nombrado en un artículo fundamental publicado en 1977 por Arthur Dempster, Nan Laird y Donald Rubin. Su trabajo formalizó el algoritmo y demostró su utilidad en el modelado y la estimación estadísticos.
en cadena en java
El algoritmo EM es aplicable a variables latentes, que son variables que no son directamente observables pero que se infieren de los valores de otras variables observadas. Aprovechando la forma general conocida de la distribución de probabilidad que rige estas variables latentes, el algoritmo EM puede predecir sus valores.
El algoritmo EM sirve como base para muchos algoritmos de agrupamiento en clústeres no supervisados en el campo del aprendizaje automático. Proporciona un marco para encontrar los parámetros locales de máxima verosimilitud de un modelo estadístico e inferir variables latentes en los casos en que faltan datos o están incompletos.
Algoritmo de maximización de expectativas (EM)
El algoritmo de Maximización de Expectativas (EM) es un método de optimización iterativo que combina diferentes métodos no supervisados. aprendizaje automático algoritmos para encontrar máxima verosimilitud o estimaciones posteriores máximas de parámetros en modelos estadísticos que involucran variables latentes no observadas. El algoritmo EM se usa comúnmente para modelos de variables latentes y puede manejar datos faltantes. Consiste en un paso de estimación (paso E) y un paso de maximización (paso M), formando un proceso iterativo para mejorar el ajuste del modelo.
- En el paso E, el algoritmo calcula las variables latentes, es decir, la expectativa de probabilidad logarítmica utilizando las estimaciones de los parámetros actuales.
- En el paso M, el algoritmo determina los parámetros que maximizan la probabilidad logarítmica esperada obtenida en el paso E, y los parámetros correspondientes del modelo se actualizan en función de las variables latentes estimadas.

Maximización de expectativas en el algoritmo EM
Al repetir estos pasos de forma iterativa, el algoritmo EM busca maximizar la probabilidad de los datos observados. Se usa comúnmente para tareas de aprendizaje no supervisadas, como la agrupación en clústeres, donde se infieren variables latentes y tiene aplicaciones en varios campos, incluido el aprendizaje automático, la visión por computadora y el procesamiento del lenguaje natural.
Términos clave en el algoritmo de maximización de expectativas (EM)
Algunos de los términos clave más utilizados en el algoritmo de maximización de expectativas (EM) son los siguientes:
- Variables latentes: las variables latentes son variables no observadas en los modelos estadísticos que solo pueden inferirse indirectamente a través de sus efectos sobre las variables observables. No pueden medirse directamente, pero pueden detectarse por su impacto en las variables observables. Probabilidad: Es la probabilidad de observar los datos dados dados los parámetros del modelo. En el algoritmo EM, el objetivo es encontrar los parámetros que maximicen la probabilidad. Log-Verosimilitud: Es el logaritmo de la función de verosimilitud, que mide la bondad de ajuste entre los datos observados y el modelo. El algoritmo EM busca maximizar la probabilidad logarítmica. Estimación de máxima verosimilitud (MLE): MLE es un método para estimar los parámetros de un modelo estadístico encontrando los valores de los parámetros que maximizan la función de verosimilitud, que mide qué tan bien el modelo explica los datos observados. Probabilidad posterior: en el contexto de la inferencia bayesiana, el algoritmo EM se puede ampliar para estimar las estimaciones máximas a posteriori (MAP), donde la probabilidad posterior de los parámetros se calcula en función de la distribución previa y la función de verosimilitud. Paso de expectativa (E): el paso E del algoritmo EM calcula el valor esperado o la probabilidad posterior de las variables latentes dados los datos observados y las estimaciones de los parámetros actuales. Implica calcular las probabilidades de cada variable latente para cada punto de datos. Paso de maximización (M): el paso M del algoritmo EM actualiza las estimaciones de los parámetros maximizando la probabilidad logarítmica esperada obtenida del paso E. Implica encontrar los valores de los parámetros que optimizan la función de probabilidad, generalmente mediante métodos de optimización numérica. Convergencia: la convergencia se refiere a la condición en la que el algoritmo EM ha alcanzado una solución estable. Por lo general, se determina verificando si el cambio en la probabilidad logarítmica o en las estimaciones de los parámetros cae por debajo de un umbral predefinido.
Cómo funciona el algoritmo de maximización de expectativas (EM):
La esencia del algoritmo de maximización de expectativas es utilizar los datos observados disponibles del conjunto de datos para estimar los datos faltantes y luego utilizar esos datos para actualizar los valores de los parámetros. Comprendamos el algoritmo EM en detalle.

Diagrama de flujo del algoritmo EM
- Inicialización:
- Inicialmente se considera un conjunto de valores iniciales de los parámetros. Se proporciona al sistema un conjunto de datos observados incompletos con el supuesto de que los datos observados provienen de un modelo específico.
- Calcule la probabilidad o responsabilidad posterior de cada variable latente dados los datos observados y las estimaciones de los parámetros actuales.
- Calcule los valores de datos faltantes o incompletos utilizando las estimaciones de parámetros actuales.
- Calcule la probabilidad logarítmica de los datos observados basándose en las estimaciones de los parámetros actuales y los datos faltantes estimados.
- Actualice los parámetros del modelo maximizando la probabilidad de registro de datos completos esperados obtenidos del paso E.
- Por lo general, esto implica resolver problemas de optimización para encontrar los valores de los parámetros que maximizan la probabilidad logarítmica.
- La técnica de optimización específica utilizada depende de la naturaleza del problema y del modelo que se utilice.
- Verifique la convergencia comparando el cambio en la probabilidad logarítmica o los valores de los parámetros entre iteraciones.
- Si el cambio está por debajo de un umbral predefinido, deténgase y considere que el algoritmo converge.
- De lo contrario, regrese al paso E y repita el proceso hasta lograr la convergencia.
Implementación paso a paso del algoritmo de maximización de expectativas
Importar las bibliotecas necesarias
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
Generar un conjunto de datos con dos componentes gaussianos.
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
Producción :

Gráfico de densidad
algoritmo kmp
Inicializar parámetros
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
10 millones
>
>
Realizar algoritmo EM
- Itera durante el número especificado de épocas (20 en este caso).
- En cada época, el paso E calcula las responsabilidades (valores gamma) evaluando las densidades de probabilidad gaussianas para cada componente y ponderándolas según las proporciones correspondientes.
- El paso M actualiza los parámetros calculando la media ponderada y la desviación estándar para cada componente.
Python3
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
importar escáner java
>
>
Producción :

Época vs probabilidad logarítmica
Trazar la densidad estimada final.
Python3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Producción :
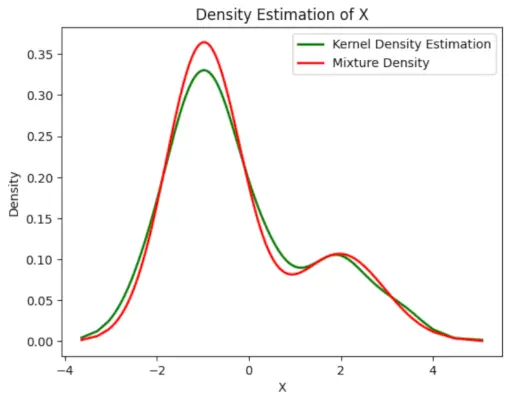
Densidad estimada
Aplicaciones de la algoritmo EM
- Se puede utilizar para completar los datos que faltan en una muestra.
- Puede utilizarse como base para el aprendizaje no supervisado de clústeres.
- Puede utilizarse con el fin de estimar los parámetros del modelo oculto de Markov (HMM).
- Puede utilizarse para descubrir los valores de variables latentes.
Ventajas del algoritmo EM
- Siempre se garantiza que la probabilidad aumentará con cada iteración.
- Los pasos E y M suelen ser bastante sencillos para muchos problemas en términos de implementación.
- Las soluciones a los pasos M suelen existir en forma cerrada.
Desventajas del algoritmo EM
- Tiene una convergencia lenta.
- Hace convergencia únicamente al óptimo local.
- Requiere ambas probabilidades, hacia adelante y hacia atrás (la optimización numérica solo requiere probabilidad hacia adelante).
