Programación lineal es un concepto matemático que se utiliza para encontrar la solución óptima de la función lineal. Este método utiliza suposiciones simples para optimizar la función dada. La programación lineal tiene una enorme aplicación en el mundo real y se utiliza para resolver varios tipos de problemas.
La programación lineal se utiliza en diversas industrias, como la industria naviera, la industria manufacturera, la industria del transporte, las telecomunicaciones y otras.
El término programación lineal consta de dos palabras lineal y programación, la palabra lineal indica la relación entre varios tipos de variables de grado uno utilizadas en un problema y la palabra programación nos indica el procedimiento paso a paso para resolver estos problemas.
En este artículo, aprenderemos en detalle sobre programación lineal, sus ejemplos, fórmulas y otros conceptos.
Tabla de contenidos
- ¿Qué es la programación lineal?
- Componentes de la programación lineal
- Ejemplos de programación lineal
- Problemas de programación lineal
- Tipos de problemas de programación lineal
- Fórmula de programación lineal
- ¿Cómo resolver problemas de programación lineal?
- Métodos de programación lineal
- Método simplex de programación lineal
- Método gráfico de programación lineal
- Aplicaciones de programación lineal
- Importancia de la programación lineal
- Aplicaciones actualizadas de programación lineal
- Programación lineal en investigación de operaciones
- Método simplex
¿Qué es la programación lineal?
Programación lineal o Optimización lineal es una técnica que nos ayuda a encontrar la solución óptima para un problema determinado, una solución óptima es una solución que es el mejor resultado posible de un problema particular determinado.
En términos simples, es el método para descubrir cómo hacer algo de la mejor manera posible. Con recursos limitados, es necesario hacer una utilización óptima de los recursos y lograr el mejor resultado posible en un objetivo particular, como el menor costo, el mayor margen o el menor tiempo.
La situación que requiere una búsqueda de los mejores valores de las variables sujetas a ciertas restricciones es donde utilizamos problemas de programación lineal. Estas situaciones no pueden manejarse mediante el cálculo y las técnicas numéricas habituales.
Definición de programación lineal
La programación lineal es la técnica utilizada para optimizar un escenario particular. El uso de programación lineal nos proporciona el mejor resultado posible en una situación determinada. Utiliza todos los recursos disponibles de manera que produzcan el resultado óptimo.
Componentes de la programación lineal
Los componentes básicos de un problema de programación lineal (LP) son:
- Variables de decisión: Variables que se desean determinar para lograr la solución óptima.
- Función Objetivo: M Ecuación matemática que representa el objetivo que deseas alcanzar.
- Restricciones: Limitaciones o restricciones que deben seguir sus variables de decisión.
- Restricciones de no negatividad: En algunos En escenarios del mundo real, las variables de decisión no pueden ser negativas.
Características adicionales de la programación lineal
- Finitud: El número de variables de decisión y restricciones en un problema de PL es finito.
- Linealidad: La función objetivo y todas las restricciones deben ser funciones lineales de las variables de decisión. . Significa que el grado de las variables debe ser uno.
Ejemplos de programación lineal
Podemos comprender las situaciones en las que se aplica la programación lineal con la ayuda del ejemplo que se analiza a continuación.
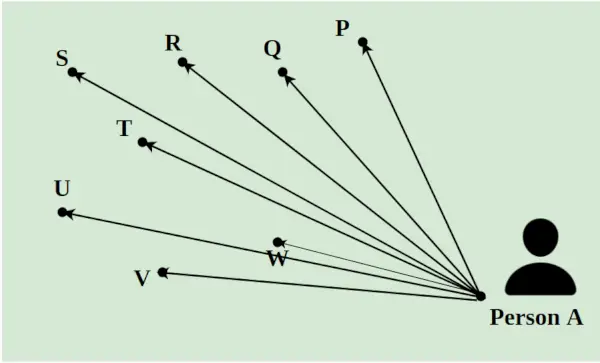
Supongamos que un repartidor tiene que entregar 8 paquetes en un día en las diferentes localidades de una ciudad. Tiene que recoger todos los paquetes de A y entregarlos en los puntos P, Q, R, S, T, U, V y W. La distancia entre ellos se indica mediante las líneas como se muestra en la imagen de abajo. El camino más corto que sigue el repartidor se calcula utilizando el concepto de Programación Lineal.
no nulo en js
Problemas de programación lineal
Problemas de programación lineal (LPP) implican optimizar una función lineal para encontrar la solución de valor óptimo para la función. El valor óptimo puede ser el valor máximo o el valor mínimo.
En LPP, las funciones lineales se llaman funciones objetivas. Una función objetivo puede tener múltiples variables, las cuales están sujetas a condiciones y deben satisfacer las restricciones lineales .
Tipos de problemas de programación lineal
Hay muchos problemas de programación lineal (LPP) diferentes, pero en este artículo nos ocuparemos de tres problemas principales de programación lineal.
Problemas de fabricación
Los problemas de fabricación son un problema que trata del número de unidades que se deben producir o vender para maximizar las ganancias cuando cada producto requiere mano de obra, horas de máquina y materias primas fijas.
Problemas de dieta
Se utiliza para calcular el número de diferentes tipos de componentes que se incluirán en la dieta para obtener el costo mínimo, sujeto a la disponibilidad de alimentos y sus precios.
Problemas de transporte
Se utiliza para determinar el cronograma de transporte y encontrar la forma más económica de transportar un producto desde plantas/fábricas situadas en diferentes lugares a diferentes mercados.
Fórmula de programación lineal
Un problema de programación lineal consiste en,
- Variables de decisión
- Función objetiva
- Restricciones
- Restricciones no negativas
Variables de decisión son las variables x, y y, que deciden el resultado del problema de programación lineal y representan la solución final.
El función objetiva , generalmente representada por Z, es la función lineal que debe optimizarse según la condición dada para obtener la solución final.
El restricciones Las restricciones impuestas a las variables de decisión que limitan sus valores se denominan restricciones.
Ahora, la fórmula general de un problema de programación lineal es,
Función objetiva : Z = hacha + por
Restricciones: cx + dy ≥ e, px + qy ≤ r
Restricciones no negativas: x ≥ 0, y ≥ 0
En la condición anterior, xey son las variables de decisión.
¿Cómo resolver problemas de programación lineal?
Antes de resolver los problemas de programación lineal, primero debemos formular los problemas de acuerdo con los parámetros estándar. Los pasos para resolver problemas de programación lineal son,
Paso 1: Marque las variables de decisión en el problema.
Paso 2: Construya la función objetivo del problema y verifique si es necesario minimizar o maximizar la función.
Paso 3: Escriba todas las restricciones de los problemas lineales.
Etapa 4: Asegurar restricciones no negativas de las variables de decisión.
Paso 5: Ahora resuelva el problema de programación lineal usando cualquier método, generalmente usamos el método simplex o gráfico.
Métodos de programación lineal
Utilizamos varios métodos para resolver problemas de programación lineal. Los dos métodos más comunes utilizados son,
- Método simplex
- Método gráfico
Aprendamos sobre estos dos métodos en detalle en este artículo.
Método simplex de programación lineal
Uno de los métodos más comunes para resolver el problema de programación lineal es el método simplex. En este método, repetimos una condición específica 'n' varias veces hasta lograr una solución óptima.
Los pasos necesarios para resolver problemas de programación lineal utilizando el método simplex son,
Paso 1: Formule los problemas de programación lineal basándose en las restricciones dadas.
Paso 2: Convierta todas las desigualdades dadas en ecuaciones o igualdades de los problemas de programación lineal agregando la variable de holgura a cada desigualdad cuando sea necesario.
Paso 3: Construya la tabla simplex inicial. Representando cada ecuación de restricción en una fila y escribiendo la función objetivo en la fila inferior. La tabla así obtenida se denomina tabla Simplex.
Etapa 4: Identifique la entrada negativa más grande en la fila inferior. La columna del elemento con la entrada negativa más alta se llama columna dinámica.
Paso 5: Divida las entradas de la columna de la derecha con las entradas de la columna dinámica respectiva, excluyendo las entradas de la fila inferior. Ahora la fila que contiene la menor entrada se llama fila dinámica. El elemento pivote se obtiene mediante la intersección de la fila pivote y la columna pivote.
Paso 6: Usando la operación matricial y con la ayuda del elemento pivote, haga que todas las entradas en la columna dinámica sean cero.
Paso 7: Verifique las entradas no negativas en la fila inferior; si no hay entradas negativas en la fila inferior, finalice el proceso; de lo contrario, comience el proceso nuevamente desde el paso 4.
Paso 8: La tabla simplex final así obtenida da la solución a nuestro problema.
Método gráfico de programación lineal
El método gráfico es otro método además del método Simplex que se utiliza para resolver problemas de programación lineal. Como sugiere el nombre, este método utiliza gráficos para resolver los problemas de programación lineal dados. Este es el mejor método para resolver problemas de programación lineal y requiere menos esfuerzo que el método simplex.
Al utilizar este método, trazamos todas las desigualdades que están sujetas a restricciones en los problemas de programación lineal dados. Tan pronto como todas las desigualdades del LPP dado se representan en el gráfico XY, la región común de todas las desigualdades da la solución óptima. Se calculan todos los puntos de las esquinas de la región factible y se calcula el valor de la función objetivo en todos esos puntos, luego, comparando estos valores, obtenemos la solución óptima del LPP.
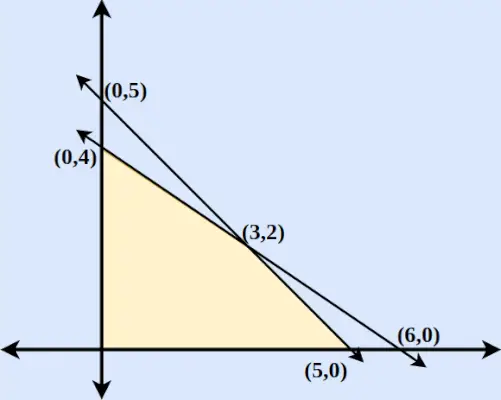
Ejemplo: Encuentre el valor máximo y mínimo de z = 6x + 9y cuando las condiciones de restricción son,
- 2x + 3y ≤ 12
- x e y ≥ 0
- x + y ≤ 5
Solución:
Paso 1 : Primero convierta las inecuaciones en ecuaciones normales. Por tanto las ecuaciones serán 2x+3y = 0, x = 0, y = 0 y x + y = 5.
Paso 2 : Encuentre los puntos en los cuales 2x + 3y y x + y = 5 cortan el eje x y el eje y. Para encontrar el punto de intersección del eje x ponga y = 0 en la ecuación respectiva y encuentre el punto. De manera similar, para los puntos de intersección del eje y, coloque x = 0 en la ecuación respectiva.
Paso 3 : Dibuja las dos líneas que cortan el eje x y el eje y. Encontramos que los dos ejes se cortan en (3,2).
Etapa 4 : Para x ≥ 0 y y ≥ 0, encontramos que se siguen ambas inecuaciones. Por lo tanto, la región incluirá una región de área encerrada por dos ejes y ambas líneas incluirán el origen. La región trazada se muestra a continuación en la figura.
Paso 5 : Encuentre Z para cada punto y máximos y mínimos.
Coordenadas Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Por tanto, encontramos que Z = 6x + 9y es máximo en (0,5) y mínimo en (5,0).
Aplicaciones de programación lineal
La Programación Lineal tiene aplicaciones en diversos campos. Se utiliza para encontrar el costo mínimo de un proceso cuando se dan todas las restricciones de los problemas. Se utiliza para optimizar el costo de transporte del vehículo, etc. Varias aplicaciones de Programación Lineal son
Industrias de ingeniería
Las industrias de ingeniería utilizan la programación lineal para resolver problemas de diseño y fabricación y obtener el máximo rendimiento de una condición determinada.
Industrias manufactureras
Las industrias manufactureras utilizan la programación lineal para maximizar las ganancias de las empresas y reducir el costo de fabricación.
Industrias energéticas
Las empresas de energía utilizan la programación lineal para optimizar su producción.
Industrias del transporte
La programación lineal también se utiliza en las industrias del transporte para encontrar el camino para minimizar el costo del transporte.
Importancia de la programación lineal
La programación lineal tiene una gran importancia en diversas industrias: maximiza el valor de salida y minimiza los valores de entrada de acuerdo con diversas restricciones.
LP es altamente aplicable cuando tenemos múltiples condiciones al resolver un problema y tenemos que optimizar el resultado del problema, es decir, tenemos que encontrar el valor mínimo o máximo de acuerdo con una condición dada.
Leer más,
- Desigualdades lineales
- Solución algebraica de desigualdades lineales
Problemas de programación lineal
Problema 1: Una empresa fabrica y vende dos tipos de productos y el costo de producción de cada unidad a y b es de 200 y 150 rupias respectivamente. Cada unidad de producto genera una ganancia de 20 rupias y cada unidad de producto b genera una ganancia de 15 rupias al venderla. . La empresa estima que la demanda mensual de A y B es como máximo de la unidad cosechada en todo el presupuesto de producción para el mes se establece en 50 000 rupias. ¿Cuántas unidades debe fabricar la empresa para obtener el máximo beneficio de sus ventas mensuales de un ¿y B?
Solución:
Sea x = número de unidades del tipo A
y = Número de unidades del tipo B
Maximizar Z = 40x + 50y
Sujeto a las limitaciones
3x + y ≤ 9
x + 2y ≤ 8
y x, y ≥ 0
Considere la ecuación,
3x + y = 9
x = 3
y = 0
y x + 2y = 8
x = 8
y = 0
Ahora, podemos determinar el valor máximo de Z evaluando el valor de Z en los cuatro puntos (vértices) que se muestran a continuación.
Vértices
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
convertir string a date(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(2, 3)
Z = 40 × 2 + 50 × 3 = Rs. 230
Beneficio máximo, Z = Rs. 230
∴ El número de unidades de tipo A es 2 y el número de unidades de tipo B es 3.
Problema 2: Maximizar Z = 3x + 4y.
Sujeto a restricciones, x + y ≤ 450, 2x + y ≤ 600 y x, y ≤ 0.
Solución:
Tenemos de lo dado
Restricciones (1)
X + Y = 450
Putting x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Putting y = 0, ⇒ x + 0 = 450 ⇒ x = 450
De, Restricciones (2)
2x + y = 600
Putting x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Putting y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Ahora tenemos la coordenada de puntos Z = 3x + 4y.
| Vértices | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Por lo tanto, la solución óptima es máxima Z = 1800 en las coordenadas x = 0 e y = 450. El gráfico se muestra a continuación.

Aplicaciones actualizadas de programación lineal
La programación lineal, una poderosa técnica matemática, se utiliza para resolver problemas de optimización en diversas industrias. Aquí hay algunas aplicaciones modernas:
- Optimización de la cadena de suministro : La programación lineal ayuda a las empresas a minimizar costos y maximizar la eficiencia en sus cadenas de suministro. Se utiliza para determinar las rutas de transporte, operaciones de almacén y estrategias de gestión de inventario más rentables.
- Gestión Energética : En el sector energético, la programación lineal se utiliza para optimizar la combinación de métodos de producción de energía. Esto incluye equilibrar las fuentes de energía tradicionales con las renovables para reducir los costos y el impacto ambiental y al mismo tiempo satisfacer la demanda.
- Diseño de Redes de Telecomunicaciones : La programación lineal ayuda al diseño de redes de telecomunicaciones eficientes. Ayuda a asignar ancho de banda, diseñar diseños de red y optimizar el flujo de datos para garantizar una comunicación de alta velocidad a costos más bajos.
- Planificacion Financiera : Las empresas y los analistas financieros utilizan la programación lineal para la optimización de carteras, la gestión de riesgos y la presupuestación de capital. Ayuda a tomar decisiones de inversión que maximizan la rentabilidad y minimizan el riesgo.
- Logística sanitaria : En atención médica, la programación lineal se aplica para optimizar la asignación de recursos, como camas de hospital, personal médico y equipos. Es crucial para mejorar la atención al paciente, reducir los tiempos de espera y gestionar los costos de manera efectiva.
- Optimización del proceso de fabricación : La programación lineal se utiliza para determinar los niveles de producción óptimos para múltiples productos dentro de una instalación de fabricación, considerando limitaciones como mano de obra, materiales y disponibilidad de la máquina.
- Planificación Agrícola : Los agricultores y planificadores agrícolas utilizan la programación lineal para decidir sobre la selección de cultivos, el uso de la tierra y la asignación de recursos para maximizar los rendimientos y las ganancias mientras se conservan los recursos.
- Programación de tripulación de aerolínea : Las aerolíneas emplean programación lineal para programar tripulaciones de manera eficiente, garantizando que los vuelos cuenten con personal que cumpla con las regulaciones y minimizando los costos operativos.
Estas aplicaciones demuestran la versatilidad y el poder de la programación lineal para resolver problemas complejos de optimización en varios sectores, mostrando su relevancia en el mundo actual basado en datos.
Programación lineal en investigación de operaciones
- Herramienta principal : La programación lineal es una herramienta fundamental en la investigación de operaciones para optimizar recursos.
- Toma de decisiones : Ayuda a tomar las mejores decisiones con respecto a la asignación de recursos, maximizar las ganancias o minimizar los costos.
- Amplias aplicaciones : Se utiliza en diversos campos, como logística, fabricación, finanzas y atención médica, para resolver problemas complejos.
- Modelado de problemas del mundo real : Transforma problemas del mundo real en modelos matemáticos para encontrar las soluciones más eficientes.
Método simplex
- Algoritmo de optimización : El Método Simplex es un poderoso algoritmo utilizado en programación lineal para encontrar la solución óptima a desigualdades lineales.
- Enfoque paso a paso : avanza iterativamente hacia la mejor solución navegando por los bordes de la región factible definida por restricciones.
- Eficiencia : Conocido por su eficiencia en la resolución de problemas de programación lineal a gran escala.
- Versatilidad : Aplicable en varios dominios como planificación de dietas, flujos de red, programación de producción y más, lo que demuestra su versatilidad.
Programación lineal: preguntas frecuentes
¿Qué es la programación lineal?
La programación lineal es un concepto matemático que se utiliza para optimizar un problema lineal dado que tiene una variedad de restricciones. Usando programación lineal obtenemos el resultado óptimo del problema dado.
¿Qué son los problemas de programación lineal?
Los problemas de programación lineal (LPP) son los problemas que dan la solución óptima a las condiciones dadas.
¿Qué es la fórmula de programación lineal?
Las fórmulas generales de programación lineal son,
- Función Objetivo: Z = ax + by
- Restricciones: px + qy ≤ r, sx + ty ≤ u
- Restricciones no negativas: x ≥ 0, y ≥ 0
¿Cuáles son los diferentes tipos de programación lineal?
Los diferentes tipos de métodos de programación lineal son,
- Programación lineal por método simplex
- Programación lineal por el método R
- Programación lineal por método gráfico
¿Cuáles son los requisitos de la programación lineal?
Varios requisitos de los problemas de programación lineal son,
- Linealidad
- Función objetiva
- Restricciones
- No negatividad
¿Cuáles son las ventajas de la Programación Lineal?
Varias ventajas de la programación lineal son,
- Proporciona la solución óptima a cualquier problema lineal dado.
- Es fácil de usar y siempre da resultados consistentes.
- Ayuda a maximizar los beneficios y reducir el coste de los insumos.