¿Todo rectángulo es un rombo? Un rectángulo es una figura geométrica bidimensional representada por cuatro lados y cuatro esquinas. Un rectángulo contiene lados tales que la longitud de los lados opuestos es igual y estos lados son paralelos entre sí. Los lados comparten una esquina de lados adyacentes con un ángulo de 90° entre ellos. Por lo tanto, hay cuatro ángulos rectos en el rectángulo.

Tabla de contenidos
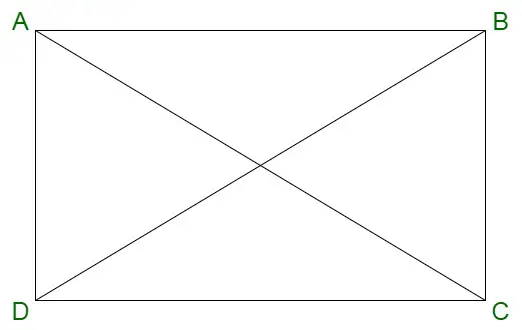
Rectángulo
Las propiedades de un rectángulo se dan a continuación:
- Tiene cuatro aristas y cuatro esquinas, conocidas como vértices.
- Las diagonales de un rectángulo se bisecan entre sí.
- El área de un rectángulo es equivalente al producto de su largo por su ancho.
- Cada vértice tiene un ángulo igual a 90.oh
- Los lados opuestos de un rectángulo son iguales y paralelos entre sí.
- El perímetro equivale al doble de la suma de su largo y ancho.
- La suma de todos los ángulos interiores es igual a 360 grados.
Perímetro de un rectángulo
El desplazamiento total cubierto al atravesar el límite del rectángulo se puede denominar perímetro. Dado que tanto el largo como el ancho se indican en unidades de longitud, el perímetro también se mide en unidades de longitud.
El perímetro se puede denotar por,
Perímetro, P = 2 (Largo + Ancho)
Área del rectángulo
La región que abarca una figura geométrica bidimensional en un plano se llama área de una figura. Por tanto, el área de un rectángulo es el área incluida dentro de sus límites. Se mide en unidades cuadradas. El área es equivalente al producto del largo por el ancho del rectángulo.
El área se puede denotar por,
Área, A = Largo × Ancho unidades cuadradas
Fórmula de la diagonal de un rectángulo
Las diagonales de cualquier figura geométrica conectan vértices alternos. La longitud de las diagonales de un rectángulo se puede calcular mediante la siguiente fórmula, denotada por d,
d = sqrt{( l^2 + w^2)} dónde,
l = longitud del rectángulo
w = ancho del rectángulo
Leer en detalle: Propiedades del rectángulo: definición, fórmulas, ejemplos
Rombo
Un rombo también se conoce como cuadrilátero de cuatro lados. Se considera un caso especial de paralelogramo. Un rombo contiene lados opuestos paralelos y ángulos opuestos iguales. Un rombo también se conoce con el nombre de diamante o diamante rombo. Un rombo contiene todos los lados de un rombo con la misma longitud. Además, las diagonales de un rombo se bisecan formando ángulos rectos.
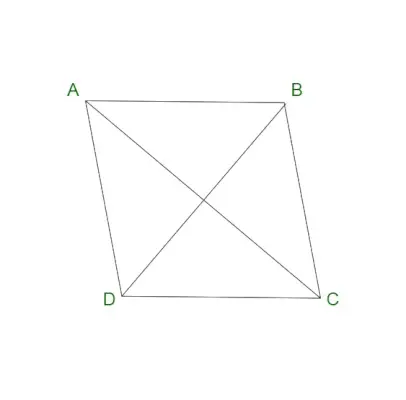
Propiedades de un rombo
Un rombo contiene las siguientes propiedades:
- Un rombo contiene todos los lados iguales.
- Las diagonales de un rombo se bisecan formando ángulos rectos.
- Los lados opuestos de un rombo son de naturaleza paralela.
- La suma de dos ángulos adyacentes de un rombo es igual a 180.oh.
- No hay ningún círculo de inscripción dentro de un rombo.
- No existe un círculo que circunscriba un rombo.
- Las diagonales de un rombo dan lugar a la formación de cuatro triángulos rectángulos.
- Estos triángulos son congruentes entre sí.
- Los ángulos opuestos de un rombo son iguales.
- Cuando conectas el punto medio de los lados de un rombo, se forma un rectángulo.
- Cuando se conectan los puntos medios de la mitad de la diagonal, se forma otro rombo.
Perímetro del rombo
El perímetro de un rombo se define como la longitud total de sus límites que forman la figura. También se puede denotar como la suma total de la longitud de los cuatro lados de un rombo. El perímetro de un rombo está definido por:
Perímetro, P = 4a unidades
donde las diagonales del rombo se denotan por d1& d2y 'a' es el lado.
Área de rombo
El área del rombo se define como la región encerrada dentro de un plano bidimensional. El área de un rombo es equivalente al producto de las diagonales del rombo dividido por 2. El área del rombo se puede definir mediante la siguiente fórmula:
Área, A =
frac{(d_1 imes d_2)}{2} unidades cuadradasdonde D1y d2son las diagonales de un rombo.
Podemos notar fácilmente que todo rombo es un paralelogramo, pero lo contrario no es cierto. Un cuadrado puede considerarse como un caso especial de rombo ya que contiene cuatro lados de igual longitud. Un cuadrado tiene todos los ángulos rectos. Sin embargo, no todos los ángulos de un rombo son necesariamente ángulos rectos. . En conclusión, un rombo que contiene ángulos rectos puede considerarse un cuadrado. Por tanto, podemos decir que,
- Todos los rombos son paralelogramos.
- No todos los paralelogramos son rombos.
- No todos los rombos son cuadrados.
- Todos los cuadrados son rombos.
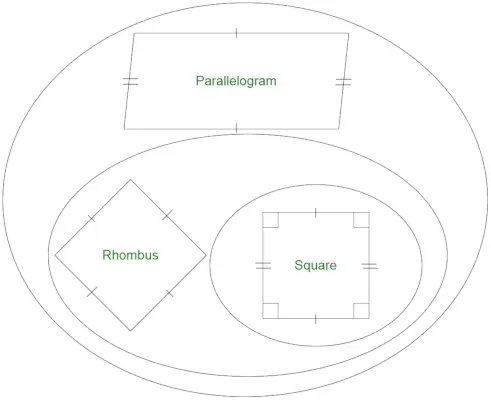
¿Todo rectángulo es un rombo?
Un rectángulo es una figura geométrica que no tiene todos los lados iguales. Un cuadrado es un caso especial de rectángulo con todos los lados iguales. Ya que sabemos que un rombo tiene todos los lados iguales. Los conjuntos de rectángulos y rombos sólo se cruzan en el caso de los cuadrados. Por tanto, el rectángulo no es un rombo.
rebanar java

¿Por qué un rombo es un rectángulo?
Un rombo es un caso especial de rectángulo. Ya que sabemos que las diagonales de un rombo se cortan en ángulos iguales mientras que las diagonales de un rectángulo tienen la misma longitud. Al conectar los puntos medios de los lados de un rombo, se forma un rectángulo.
Leer más: ¿Por qué un rombo no es un cuadrado?
Preguntas de ejemplo: ¿Todo rectángulo es un rombo?
Pregunta 1. Calcule el área de un marco rectangular, que tiene 6 pulgadas de ancho. de largo y mide 3 pulgadas de ancho.
Solución:
Ya que sabemos,
Área de un rectángulo = (largo × ancho) unidades cuadradas.
Sustituyendo los valores obtenemos
el área del marco rectangular = 6 × 3 = 18 pulgadas cuadradas
Pregunta 2. Encuentre la longitud de la diagonal de un rectángulo que tiene una longitud de 12 cm y un ancho de 8 cm respectivamente.
Solución:
Sabemos,
longitud diagonal,
re =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Pregunta 3. Encuentra el área de un rombo con las dos longitudes diagonales d 1 y d 2 ser de 6 cm y 12 cm, respectivamente.
Solución:
Tenemos,
Diagonal d1= 6cm
Diagonal d2= 12 cm
El área del rombo está dada por,
Una =
frac{(d_1 imes d_2)}{2} unidades cuadradasUna =
frac{( 6 imes 12)}{2} Una =
frac{72}{2} Un = 36 cm2
Por lo tanto, el área del rombo = 36 cm.2.
Pregunta 4. ¿Diferencia entre rombo y rectángulo?
Solución:
| Propiedad | Rombo | Rectángulo |
| Lados | Lados iguales. | Los lados opuestos son iguales. |
| Diagonales | Las diagonales se bisecan a 90°. Las diagonales forman ángulos rectos en el centro. | Las diagonales se bisecan entre sí en diferentes ángulos. Un ángulo es obtuso y el otro es agudo. Las diagonales forman diferentes ángulos en el centro: un ángulo obtuso y un ángulo agudo. |
| Anglos | Los ángulos opuestos son iguales. Los ángulos adyacentes suman 180°. | Los ángulos opuestos y adyacentes son iguales. Un ángulo formado por los lados adyacentes de un rectángulo es de 90°. |
