Árbol de búsqueda binaria es una estructura de datos utilizada en informática para organizar y almacenar datos de manera ordenada. El árbol de búsqueda binaria sigue todas las propiedades del árbol binario y sus izquierda El niño contiene valores menores que el nodo padre y el bien El niño contiene valores mayores que el nodo padre. Esta estructura jerárquica permite una eficiente buscando , Inserción , y Supresión operaciones sobre los datos almacenados en el árbol.
Árbol de búsqueda binaria
estados unidos cuantas ciudades
Tabla de contenidos
- ¿Qué es el árbol de búsqueda binaria?
- Propiedades del árbol de búsqueda binaria
- Manejo de valores duplicados en el árbol de búsqueda binaria
- Operaciones realizadas en un BST
- 1. Buscando un nodo en BST
- 2. Insertar un nodo en un BST
- 3. Eliminar un nodo de BST
- 4. Recorrido (recorrido en orden de BST)
- Aplicaciones de BST
- Ventajas
- Desventajas
- Preguntas frecuentes (preguntas frecuentes) sobre el árbol de búsqueda binaria:
¿Qué es el árbol de búsqueda binaria?
Árbol de búsqueda binaria (BST) es un tipo especial de árbol binario en el que el hijo izquierdo de un nodo tiene un valor menor que el valor del nodo y el hijo derecho tiene un valor mayor que el valor del nodo. Esta propiedad se denomina propiedad BST y permite buscar, insertar y eliminar elementos en el árbol de manera eficiente.
Propiedades del árbol de búsqueda binaria:
- El subárbol izquierdo de un nodo contiene solo nodos con claves menores que la clave del nodo.
- El subárbol derecho de un nodo contiene solo nodos con claves mayores que la clave del nodo.
- Esto significa que todo lo que está a la izquierda de la raíz es menor que el valor de la raíz y todo lo que está a la derecha de la raíz es mayor que el valor de la raíz. Gracias a esta realización, la búsqueda binaria es muy sencilla.
- Los subárboles izquierdo y derecho también deben ser un árbol de búsqueda binario.
- No debe haber nodos duplicados (BST puede tener valores duplicados con diferentes enfoques de manejo)
Manejo de valores duplicados en el árbol de búsqueda binaria:
- Debemos seguir un proceso coherente en todo momento, es decir, almacenar el valor duplicado a la izquierda o almacenar el valor duplicado a la derecha de la raíz, pero sea coherente con su enfoque.
Operaciones básicas en el árbol de búsqueda binaria:
1. Buscando un nodo en BST:
Buscar en BST significa localizar un nodo específico en la estructura de datos. En el árbol de búsqueda binaria, buscar un nodo es fácil debido a su orden específico. Los pasos para buscar un nodo en el árbol de búsqueda binaria se enumeran a continuación:
- Primero, compare el elemento a buscar con el elemento raíz del árbol.
- Si la raíz coincide con el elemento de destino, devuelve la ubicación del nodo.
- Si no coincide, verifique si el elemento es menor que el elemento raíz, si es más pequeño que el elemento raíz, muévase al subárbol izquierdo.
- Si es más grande que el elemento raíz, muévase al subárbol derecho.
- Repita el procedimiento anterior de forma recursiva hasta encontrar la coincidencia.
- Si el elemento no se encuentra o no está presente en el árbol, devuelve NULL.
Ahora, comprendamos la búsqueda en árbol binario usando un ejemplo:
A continuación se proporciona un BST y tenemos que buscar el elemento 6.
Código:
A continuación se muestra la implementación de la búsqueda en BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Una función de utilidad para insertar // un nuevo nodo con la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL ) devolver nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) nodo->izquierda = insertar(nodo->izquierda, clave); else if (clave> nodo->clave) nodo->derecha = insertar(nodo->derecha, clave); // Devuelve el puntero del nodo (sin cambios) return node; } // Función de utilidad para buscar una clave en un BST struct node* search(struct node* root, int key) root->key == key) return root; // La clave es mayor que la clave de root si (root->key< key) return search(root->llave correcta); // La clave es más pequeña que la clave de root return search(root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Una función de utilidad para insertar // un nuevo nodo con la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL ) devolver nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) nodo->izquierda = insertar(nodo->izquierda, clave); else if (clave> nodo->clave) nodo->derecha = insertar(nodo->derecha, clave); // Devuelve el puntero del nodo (sin cambios) return node; } // Función de utilidad para buscar una clave en un nodo de estructura BST* search(struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>nodo.clave) nodo.derecha = insertar(nodo.derecha, clave); // Devuelve el puntero del nodo (sin cambios) return node; } // Función de utilidad para buscar una clave en una búsqueda de nodo BST (raíz de nodo, clave int) // Casos base: la raíz es nula o la clave está presente en la raíz si (root == null> Pitón # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Devuelve el puntero de nodo (sin cambios) return node # Función de utilidad para buscar una clave en una búsqueda BST def (raíz, clave): # Casos base: la raíz es nulo o la clave está presente en la raíz si la raíz es Ninguna o root.key == clave: devuelve la raíz # La clave es mayor que la clave de la raíz si root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
javascript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>nodo.clave) { nodo.derecha = insertar(nodo.derecha, clave); } // Devuelve el puntero del nodo (sin cambios) return node; } // Función de utilidad para buscar una clave en una función BST search(root, key) { // Casos base: la raíz es nula o la clave está presente en la raíz if (root === null || root.key === key ) {retornar raíz; } // La clave es mayor que la clave de root si (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Insertar un nodo en un BST :
Siempre se inserta una nueva llave en la hoja. Comience a buscar una clave desde la raíz hasta un nodo hoja. Una vez que se encuentra un nodo hoja, el nuevo nodo se agrega como hijo del nodo hoja.
Código:
A continuación se muestra la implementación de la inserción de un único nodo en el árbol de búsqueda binaria:
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Función para insertar un nuevo nodo con // la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL) return nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) { nodo->izquierda = insertar(nodo->izquierda, clave); } else if (clave> nodo->clave) { nodo->derecha = insertar(nodo->derecha, clave); } // Devuelve el puntero del nodo return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Función para insertar un nuevo nodo con // la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL) return nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) { nodo->izquierda = insertar(nodo->izquierda, clave); } else if (clave> nodo->clave) { nodo->derecha = insertar(nodo->derecha, clave); } // Devuelve el puntero del nodo return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>nodo.clave) { nodo.derecha = insertar(nodo.derecha, clave); } // Devuelve el nodo return node; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Devuelve el puntero del nodo return node>
JavaScript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>nodo.clave) { nodo.derecha = insertar(nodo.derecha, clave); } // Devuelve el puntero del nodo return node; }> Complejidad del tiempo: O(N), donde N es el número de nodos del BST
Espacio Auxiliar: O(1)
3. Eliminar un nodo de BST :
Se utiliza para eliminar un nodo con una clave específica del BST y devolver el nuevo BST.
Diferentes escenarios para eliminar el nodo:
normalización en base de datos
El nodo que se va a eliminar es el nodo hoja. :
Es simple, puedes simplemente anularlo.
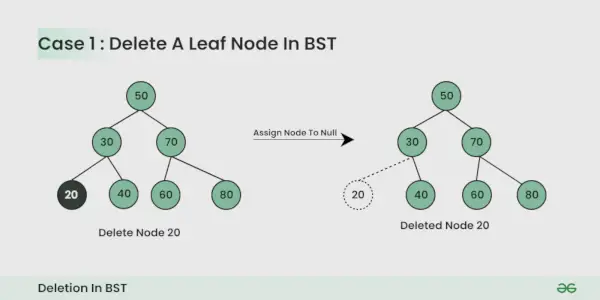
El nodo que se va a eliminar tiene un hijo :
Puede simplemente reemplazar el nodo con el nodo secundario.
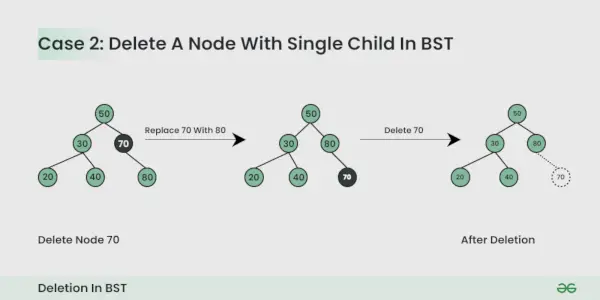
El nodo que se va a eliminar tiene dos hijos :
Aquí tenemos que eliminar el nodo es de tal manera que el árbol resultante sigue las propiedades de un BST. El truco consiste en encontrar el sucesor en orden del nodo. Copie el contenido del sucesor de orden al nodo y elimine el sucesor de orden.
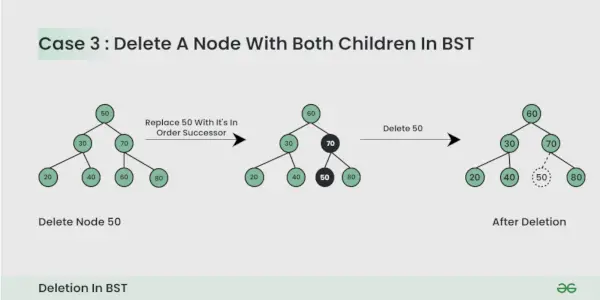
Tenga cuidado de lo siguiente al eliminar un nodo de un BST:
- Es necesario averiguar cuál será el reemplazo del nodo que se eliminará.
- Quiere una interrupción mínima de la estructura del árbol existente
- Puede tomar el nodo de reemplazo del subárbol izquierdo o derecho de los nodos eliminados.
- Si tomamos if del subárbol izquierdo, tenemos que tomar el valor más grande en el subárbol izquierdo.
- Si tomamos if del subárbol derecho, tenemos que tomar el valor más pequeño en el subárbol derecho.
Código:
A continuación se muestra la implementación de la eliminación en BST:
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Función para insertar un nuevo nodo con // la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL) return nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) { nodo->izquierda = insertar(nodo->izquierda, clave); } else if (clave> nodo->clave) { nodo->derecha = insertar(nodo->derecha, clave); } // Devuelve el puntero del nodo return node; } // Función que devuelve el nodo con // valor clave mínimo encontrado en ese árbol struct node* minValueNode(struct node* node) { struct node* current = node; // Recorre hacia abajo para encontrar la hoja más a la izquierda while (current && current->left != NULL) current = current->left; corriente de retorno; } // Función que elimina la clave y // devuelve la nueva raíz struct node* deleteNode(struct node* root, int key) { // caso base if (root == NULL) return root; // Si la clave que se va a eliminar es // más pequeña que la clave de la raíz, // entonces se encuentra en el subárbol izquierdo if (key< root->clave) { raíz->izquierda = eliminarNodo(raíz->izquierda, clave); } // Si la clave que se va a eliminar es // mayor que la clave de la raíz, // entonces se encuentra en el subárbol derecho else if (clave> raíz->clave) { raíz->derecha = eliminarNodo(raíz-> llave correcta); } // Si la clave es la misma que la clave de root, // entonces este es el nodo // que se eliminará else { // Nodo con un solo hijo // o ningún hijo si (root->left == NULL) { estructura nodo* temp = raíz->derecha; gratis (raíz); temperatura de retorno; } else if (raíz->derecha == NULL) { estructura nodo* temp = raíz->izquierda; gratis (raíz); temperatura de retorno; } // Nodo con dos hijos: // Obtiene el sucesor en orden (el más pequeño // en el subárbol derecho) struct node* temp = minValueNode(root->right); // Copia el contenido del sucesor del orden // a este nodo root->key = temp->key; // Eliminar el sucesor del orden root->right = deleteNode(root->right, temp->key); } devolver raíz; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Función para insertar un nuevo nodo con // la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL) return nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) { nodo->izquierda = insertar(nodo->izquierda, clave); } else if (clave> nodo->clave) { nodo->derecha = insertar(nodo->derecha, clave); } // Devuelve el puntero del nodo return node; } // Función que devuelve el nodo con // valor clave mínimo encontrado en ese árbol struct node* minValueNode(struct node* node) { struct node* current = node; // Recorre hacia abajo para encontrar la hoja más a la izquierda while (current && current->left != NULL) current = current->left; corriente de retorno; } // Función que elimina la clave y // devuelve la nueva raíz struct node* deleteNode(struct node* root, int key) { // caso base if (root == NULL) return root; // Si la clave que se va a eliminar es // más pequeña que la clave de la raíz, // entonces se encuentra en el subárbol izquierdo if (key< root->clave) { raíz->izquierda = eliminarNodo(raíz->izquierda, clave); } // Si la clave que se va a eliminar es // mayor que la clave de la raíz, // entonces se encuentra en el subárbol derecho else if (clave> raíz->clave) { raíz->derecha = eliminarNodo(raíz-> llave correcta); } // Si la clave es la misma que la clave de root, // entonces este es el nodo // que se eliminará else { // Nodo con un solo hijo // o ningún hijo si (root->left == NULL) { estructura nodo* temp = raíz->derecha; gratis (raíz); temperatura de retorno; } else if (raíz->derecha == NULL) { estructura nodo* temp = raíz->izquierda; gratis (raíz); temperatura de retorno; } // Nodo con dos hijos: // Obtiene el sucesor en orden (el más pequeño // en el subárbol derecho) struct node* temp = minValueNode(root->right); // Copia el contenido del sucesor del orden // a este nodo root->key = temp->key; // Eliminar el sucesor del orden root->right = deleteNode(root->right, temp->key); } devolver raíz; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>nodo.clave) { nodo.derecha = insertar(nodo.derecha, clave); } // Devuelve el nodo return node; } // Función que devuelve el nodo con // valor clave mínimo encontrado en ese árbol static node minValueNode(nodo nodo) { nodo actual = nodo; // Recorre hacia abajo para encontrar la hoja más a la izquierda while (current!= null && current.left!= null) current = current.left; corriente de retorno; } // Función que elimina la clave y // devuelve el nuevo nodo estático raíz eliminarNodo(raíz del nodo, int clave) { // Caso base if (root == null) return root; // Si la clave que se va a eliminar es // más pequeña que la clave de la raíz, // entonces se encuentra en el subárbol izquierdo if (key< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>raíz.clave) { raíz.derecha = eliminarNodo(raíz.derecha, clave); } // Si la clave es la misma que la clave de root, // entonces este es el nodo // que se eliminará else { // Nodo con un solo hijo // o ningún hijo if (root.left == null) { temperatura del nodo = root.right; temperatura de retorno; } else if (root.right == null) { temperatura del nodo = root.left; temperatura de retorno; } // Nodo con dos hijos: // Obtener el sucesor en orden (el más pequeño // en el subárbol derecho) nodo temp = minValueNode(root.right); // Copia el contenido del sucesor // del orden en este nodo root.key = temp.key; // Eliminar el sucesor del orden root.right = deleteNode(root.right, temp.key); } devolver raíz; }> Pitón # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Devuelve el puntero del nodo return root # Función para realizar un recorrido en orden de BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Función que devuelve el nodo con # valor de clave mínimo encontrado en ese árbol def minValueNode(node): current = node # Recorre hacia abajo para encontrar la hoja más a la izquierda mientras estás actual y current.left no es Ninguno: current = current.left return current # Función que elimina la clave y # devuelve la nueva raíz def eliminarNodo(raíz, clave): # base Caso si la raíz es Ninguna: devuelve raíz # Si la clave será eliminado es # más pequeño que la clave de la raíz, # entonces se encuentra en el subárbol izquierdo si la clave< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = eliminarNodo(root.right, clave) # Si la clave es la misma que la clave de root, # entonces este es el nodo # que se eliminará; de lo contrario: # Nodo con un solo hijo # o sin hijo si root.left es Ninguno: temp = root.right root = Ninguno return temp elif root.right es Ninguno: temp = root.left root = Ninguno return temp # Nodo con dos hijos: # Obtener el sucesor en orden (el número más pequeño en el subárbol derecho) temp = minValueNode(root.right) # Copiar el contenido del sucesor del orden # a este nodo root.key = temp.key # Eliminar el sucesor del orden root.right = eliminarNodo(root.right, temp.key) devolver raíz>
4. Recorrido (recorrido en orden de BST) :
En el caso de árboles de búsqueda binarios (BST), el recorrido en orden proporciona nodos en orden no decreciente. Primero visitamos al hijo izquierdo, luego a la raíz y luego al hijo derecho.
A continuación se muestra la implementación de cómo realizar un recorrido en orden de un árbol de búsqueda binaria:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Función para insertar un nuevo nodo con // la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL) return nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) { nodo->izquierda = insertar(nodo->izquierda, clave); } else if (clave> nodo->clave) { nodo->derecha = insertar(nodo->derecha, clave); } // Devuelve el puntero del nodo return node; } // Función para realizar un recorrido en orden de BST void inorder(struct node* root) { if (root!= NULL) { inorder(root->left); corte<< ' ' << root->llave; inorder(raíz->derecha); } } // Código del controlador int main() { /* Creemos el siguiente BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Creando el BST root = insert(root, 50); insertar(raíz, 30); insertar(raíz, 20); insertar(raíz, 40); insertar(raíz, 70); insertar(raíz, 60); insertar(raíz, 80); // Llamada a función inorder(root); devolver 0; } // Este código es una contribución de shivanisinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clave = elemento; temperatura->izquierda = temperatura->derecha = NULL; temperatura de retorno; } // Función para insertar un nuevo nodo con // la clave dada en BST struct node* insert(struct node* node, int key) { // Si el árbol está vacío, devuelve un nuevo nodo if (node == NULL) return nuevoNodo(clave); // De lo contrario, recurra hacia abajo en el árbol if (clave< node->clave) { nodo->izquierda = insertar(nodo->izquierda, clave); } else if (clave> nodo->clave) { nodo->derecha = insertar(nodo->derecha, clave); } // Devuelve el puntero del nodo return node; } // Función para realizar un recorrido en orden de BST void inorder(struct node* root) { if (root!= NULL) { inorder(root->left); printf('%d ', raíz->clave); inorder(raíz->derecha); } } // Código del controlador int main() { /* Creemos el siguiente BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Creando el BST root = insert(root, 50); insertar(raíz, 30); insertar(raíz, 20); insertar(raíz, 40); insertar(raíz, 70); insertar(raíz, 60); insertar(raíz, 80); // Llamada a función inorder(root); devolver 0; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>nodo.clave) { nodo.derecha = insertar(nodo.derecha, clave); } // Devuelve el nodo return node; } // Función para realizar un recorrido en orden de BST static void inorder(raíz del nodo) { if (root!= null) { inorder(root.left); System.out.print(' ' + root.key); orden(raíz.derecha); } } // Código del controlador public static void main(String[] args) { /* Creemos el siguiente BST 50 / 30 70 / / 20 40 60 80 */ node root = null; // insertando valor 50 raíz = insertar(raíz, 50); // insertando valor 30 insert(raíz, 30); // insertando el valor 20 insert(raíz, 20); // insertando valor 40 insert(raíz, 40); // insertando el valor 70 insert(root, 70); // insertando el valor 60 insert(root, 60); // insertando el valor 80 insert(root, 80); // imprime el orden BST (raíz); } } // Este código es una contribución de abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Devuelve el puntero del nodo return node # Función para realizar un recorrido en orden de BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Código de controlador if __name__ == '__main__': # Creemos el siguiente BST # 50 # / # 30 70 # / / # 20 40 60 80 raíz = Ninguno # Creando el BST raíz = insertar(raíz, 50) insertar(raíz, 30) insertar(raíz, 20) insertar(raíz, 40) insertar(raíz, 70) insertar(raíz, 60) insertar(raíz , 80) # Orden de llamada a función (raíz) #Este código es una contribución de japmeet01>
Producción
20 30 40 50 60 70 80>
Complejidad del tiempo: O(N), donde N es el número de nodos del BST
Espacio Auxiliar: O(1)
Aplicaciones de BST:
- Algoritmos gráficos: Los BST se pueden utilizar para implementar algoritmos de gráficos, como en algoritmos de árbol de expansión mínima.
- Colas prioritarias: Los BST se pueden utilizar para implementar colas de prioridad, donde el elemento con mayor prioridad está en la raíz del árbol y los elementos con menor prioridad se almacenan en los subárboles.
- Árbol de búsqueda binario autoequilibrado: Los BST se pueden utilizar como estructuras de datos autoequilibradas, como el árbol AVL y el árbol rojo-negro.
- Almacenamiento y recuperación de datos: Las BST se pueden utilizar para almacenar y recuperar datos rápidamente, como en bases de datos, donde la búsqueda de un registro específico se puede realizar en tiempo logarítmico.
Ventajas:
- Búsqueda rápida: La búsqueda de un valor específico en un BST tiene una complejidad temporal promedio de O (log n), donde n es el número de nodos en el árbol. Esto es mucho más rápido que buscar un elemento en una matriz o lista vinculada, que tiene una complejidad temporal de O(n) en el peor de los casos.
- Recorrido en orden: Los BST se pueden recorrer en orden, lo que visita el subárbol izquierdo, la raíz y el subárbol derecho. Esto se puede utilizar para ordenar un conjunto de datos.
- Espacio eficiente: Los BST ahorran espacio ya que no almacenan información redundante, a diferencia de las matrices y las listas vinculadas.
Desventajas:
- Árboles torcidos: Si un árbol se sesga, la complejidad temporal de las operaciones de búsqueda, inserción y eliminación será O(n) en lugar de O(log n), lo que puede hacer que el árbol sea ineficiente.
- Tiempo adicional requerido: Los árboles autoequilibrados requieren tiempo adicional para mantener el equilibrio durante las operaciones de inserción y eliminación.
- Eficiencia: Los BST no son eficientes para conjuntos de datos con muchos duplicados, ya que desperdiciarán espacio.
Preguntas frecuentes(Preguntas frecuentes)en el árbol de búsqueda binaria:
1. ¿Qué es un árbol de búsqueda binaria?
Un árbol de búsqueda binario (BST) es un árbol binario donde cada nodo del subárbol izquierdo es menor que la raíz y cada nodo del subárbol derecho tiene un valor mayor que la raíz . Las propiedades de un árbol de búsqueda binario son recursivas: si consideramos cualquier nodo como raíz, estas propiedades seguirán siendo verdaderas.
2. ¿Qué es la operación del árbol de búsqueda binaria?
Hay tres operaciones principales en el árbol de búsqueda binaria: 1. Inserción, 2. Eliminación, 3. Búsqueda. Debido a sus propiedades, es eficaz buscar cualquier elemento en el árbol de búsqueda binaria.
3. ¿Qué es el árbol de búsqueda binaria y el árbol AVL?
Árbol de búsqueda binaria : Un árbol de búsqueda binario (BST) es un árbol binario donde cada nodo del subárbol izquierdo es menor que la raíz y cada nodo del subárbol derecho tiene un valor mayor que la raíz.
Árbol AVL : Los árboles de búsqueda binaria (BST) que se autoequilibran y giran automáticamente se conocen como árboles AVL.
4. ¿Cuáles son los usos del árbol de búsqueda binaria?
Los árboles de búsqueda binaria se pueden utilizar para implementar tipos de datos abstractos como conjuntos dinámicos, tablas de búsqueda y colas de prioridad, y utilizado en algoritmos de clasificación como la clasificación de árboles.
edad de vicky kaushal
5. ¿Cuál es la diferencia entre árbol de búsqueda binario y árbol binario?
Un árbol de búsqueda binaria es un árbol que sigue algún orden para organizar los elementos, mientras que el árbol binario no sigue ningún orden.
Artículos relacionados:
- Aplicación de BST
- Aplicaciones, ventajas y desventajas del árbol de búsqueda binaria
- Inserción en árbol de búsqueda binaria (BST)
- Búsqueda en el árbol de búsqueda binaria (BST)
- Eliminación en el árbol de búsqueda binaria (BST)
