El Código gris es una secuencia de sistemas numéricos binarios, que también se conoce como código binario reflejado . La razón para llamar a este código como código binario reflejado es que los primeros valores N/2 se comparan con los de los últimos valores N/2 en orden inverso. En este código, dos valores consecutivos se diferencian por un bit de dígitos binarios. Los códigos Gray se utilizan en la secuencia general de números binarios generados por hardware. Estos números provocan ambigüedades o errores cuando se realiza la transición de un número a su sucesivo. Este código simplemente resuelve este problema cambiando solo un bit cuando se realiza la transición entre números.
El código gris es un código muy ligero porque no depende del valor del dígito especificado por la posición. Este código también se denomina código de variable cíclica ya que la transición de un valor a su valor sucesivo conlleva un cambio de solo un bit.
¿Cómo generar código Gray?
El método de prefijo y reflexión se utilizan de forma recursiva para generar el código Gray de un número. Para generar código gris:
- Encontramos el número de bits necesarios para representar un número.
- A continuación, encontramos el código para 0, es decir, 0000, que es lo mismo que binario.
- Ahora, tomamos el código anterior, es decir, 0000, y cambiamos la parte más significativa.
- Realizamos este proceso de forma solitaria hasta que no todos los códigos estén identificados de forma única.
- Si cambiando el bit más significativo encontramos el mismo código obtenido anteriormente, entonces se cambiará el segundo bit más significativo, y así sucesivamente.
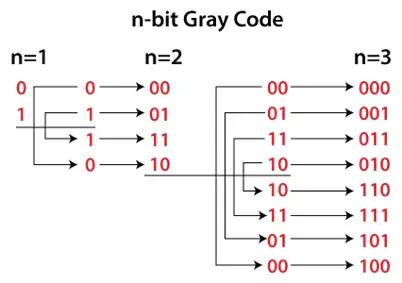
Proceso de generación de Código Gray

Tabla de códigos grises
| Número decimal | Número binario | Código gris |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
