- La máquina de estados finitos se utiliza para reconocer patrones.
- La máquina de autómatas finitos toma la cadena de símbolos como entrada y cambia su estado en consecuencia. En la entrada, cuando se encuentra el símbolo deseado, se produce la transición.
- Durante la transición, los autómatas pueden pasar al siguiente estado o permanecer en el mismo estado.
- FA tiene dos estados: aceptar estado o rechazar estado. Cuando la cadena de entrada se procese con éxito y el autómata alcance su estado final, aceptará.
Un autómata finito consta de lo siguiente:
Q: conjunto finito de estados
∑: conjunto finito de símbolo de entrada
q0: estado inicial
F: estado final
d: función de transición
La función de transición se puede definir como
δ: Q x ∑ →Q
FA se caracteriza de dos maneras:
- DFA (autómatas finitos)
- NDFA (autómatas finitos no deterministas)
DFA
DFA significa Autómata Finito Determinista. Determinista se refiere a la unicidad del cálculo. En DFA, el carácter de entrada pasa a un solo estado. DFA no acepta el movimiento nulo, lo que significa que DFA no puede cambiar de estado sin ningún carácter de entrada.
DFA tiene cinco tuplas {Q, ∑, q0, F, δ}
P: conjunto de todos los estados∑: conjunto finito de símbolo de entrada donde δ: Q x ∑ →Q
q0: estado inicial
F: estado final
d: función de transición
Ejemplo
Vea un ejemplo de autómatas finitos deterministas:
los números del alfabeto
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3} 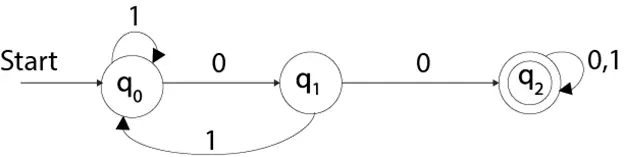
NDFA
NDFA se refiere a los autómatas finitos no deterministas. Se utiliza para transitar cualquier número de estados para una entrada en particular. NDFA acepta el movimiento NULL, lo que significa que puede cambiar de estado sin leer los símbolos.
La NDFA también tiene cinco estados al igual que la DFA. Pero el NDFA tiene una función de transición diferente.
La función de transición del NDFA se puede definir como:
d: Q x ∑ →2qEjemplo
Vea un ejemplo de autómatas finitos no deterministas:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3} 
