Camino Euleriano es un camino en un gráfico que visita cada borde exactamente una vez. El Circuito Euleriano es un Camino Euleriano que comienza y termina en el mismo vértice.


¿Cómo saber si una gráfica determinada es euleriana o no?
El problema es el mismo que el de la siguiente pregunta. ¿Es posible dibujar un gráfico determinado sin levantar el lápiz del papel y sin trazar ninguno de los bordes más de una vez?
Un grafo se llama Euleriano si tiene un Ciclo Euleriano y se llama Semieuleriano si tiene un Camino Euleriano. El problema parece similar al camino hamiltoniano, que es un problema NP completo para un gráfico general. Afortunadamente, podemos encontrar si un gráfico dado tiene un camino euleriano o no en tiempo polinomial. De hecho, podemos encontrarlo en tiempo O(V+E).
A continuación se muestran algunas propiedades interesantes de los gráficos no dirigidos con una trayectoria y un ciclo eulerianos. Podemos usar estas propiedades para encontrar si una gráfica es euleriana o no.
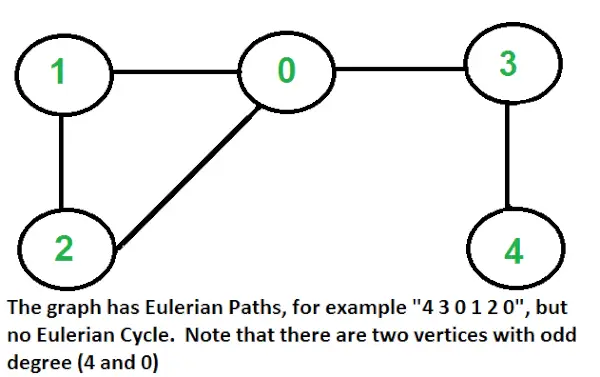
Ciclo Euleriano: Un gráfico no dirigido tiene un ciclo euleriano si se cumplen las siguientes dos condiciones.
- Todos los vértices con grados distintos de cero están conectados. No nos importan los vértices con grado cero porque no pertenecen al Ciclo o Camino Euleriano (solo consideramos todas las aristas).
- Todos los vértices tienen grado par.
Camino Euleriano: Un grafo no dirigido tiene un camino euleriano si se cumplen las siguientes dos condiciones.
- Igual que la condición (a) para el ciclo Euleriano.
- Si cero o dos vértices tienen grado impar y todos los demás vértices tienen grado par. Tenga en cuenta que solo un vértice con grado impar no es posible en un gráfico no dirigido (la suma de todos los grados siempre es par en un gráfico no dirigido)
Tenga en cuenta que un gráfico sin aristas se considera euleriano porque no hay aristas que atravesar.
encontrar mi iphone android
¿Cómo funciona esto?
En el camino euleriano, cada vez que visitamos un vértice v, caminamos a través de dos aristas no visitadas con un punto final como v. Por lo tanto, todos los vértices intermedios en el camino euleriano deben tener grados pares. Para el Ciclo Euleriano, cualquier vértice puede ser un vértice medio, por lo tanto todos los vértices deben tener grado par.
Implementación:
C++
// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> >int> V;>// No. of vertices> >list<>int>>*adjetivo;>// A dynamic array of adjacency lists> public>:> >// Constructor and destructor> >Graph(>int> V) {>this>->V = V; adj=>new> list<>int>>[EN]; }> >~Graph() {>delete> [] adj; }>// To avoid memory leak> >// function to add an edge to graph> >void> addEdge(>int> v,>int> w);> >// Method to check if this graph is Eulerian or not> >int> isEulerian();> >// Method to check if all non-zero degree vertices are connected> >bool> isConnected();> >// Function to do DFS starting from v. Used in isConnected();> >void> DFSUtil(>int> v,>bool> visited[]);> };> void> Graph::addEdge(>int> v,>int> w)> {> >adj[v].push_back(w);> >adj[w].push_back(v);>// Note: the graph is undirected> }> void> Graph::DFSUtil(>int> v,>bool> visited[])> {> >// Mark the current node as visited and print it> >visited[v] =>true>;> >// Recur for all the vertices adjacent to this vertex> >list<>int>>::iterador i;> >for> (i = adj[v].begin(); i != adj[v].end(); ++i)> >if> (!visited[*i])> >DFSUtil(*i, visited);> }> // Method to check if all non-zero degree vertices are connected.> // It mainly does DFS traversal starting from> bool> Graph::isConnected()> {> >// Mark all the vertices as not visited> >bool> visited[V];> >int> i;> >for> (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) devolver falso; devolver verdadero; } /* La función devuelve uno de los siguientes valores 0 --> Si la gráfica no es euleriana 1 --> Si la gráfica tiene una ruta de Euler (Semi-Eulerian) 2 --> Si la gráfica tiene un circuito de Euler (Eulerian) */ int Graph::isEulerian() { // Comprobar si todos los vértices de grados distintos de cero están conectados if (isConnected() == false) return 0; // Contar vértices con grado impar int odd = 0; for (int i = 0; i if (adj[i].size() & 1) odd++; // Si el recuento es mayor que 2, entonces la gráfica no es euleriana if (odd> 2) return 0; // Si es impar el recuento es 2, entonces semi-eulerian. // Si el recuento impar es 0, entonces eulerian // Tenga en cuenta que el recuento impar nunca puede ser 1 para el retorno de gráfico no dirigido (impar } // Función para ejecutar casos de prueba void? prueba(Gráfico &g) { int res = g.isEulerian(); if (res == 0) cout<< 'graph is not Eulerian
'; else if (res == 1) cout << 'graph has a Euler path
'; else cout << 'graph has a Euler cycle
'; } // Driver program to test above function int main() { // Let us create and test graphs shown in above figures Graph g1(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); test(g1); Graph g2(5); g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); test(g2); Graph g3(5); g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); test(g3); // Let us create a graph with 3 vertices // connected in the form of cycle Graph g4(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); test(g4); // Let us create a graph with all vertices // with zero degree Graph g5(3); test(g5); return 0; }> |
>
>
Java
javed urfi
// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> >private> int> V;>// No. of vertices> >// Array of lists for Adjacency List Representation> >private> LinkedList adj[];> >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> LinkedList[v];> >for> (>int> i=>0>; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) devolver falso; devolver verdadero; } /* La función devuelve uno de los siguientes valores 0 --> Si la gráfica no es euleriana 1 --> Si la gráfica tiene una ruta de Euler (Semi-Eulerian) 2 --> Si la gráfica tiene un circuito de Euler (Eulerian) */ int isEulerian() { // Comprobar si todos los vértices de grados distintos de cero están conectados if (isConnected() == false) return 0; // Contar vértices con grado impar int odd = 0; for (int i = 0; i if (adj[i].size()%2!=0) odd++; // Si el recuento es mayor que 2, entonces la gráfica no es euleriana if (odd> 2) return 0; / / Si el recuento impar es 2, entonces semi-eulerian. // Si el recuento impar es 0, entonces eulerian // Tenga en cuenta que el recuento impar nunca puede ser 1 para el retorno de gráfico no dirigido (odd==2)? Función para ejecutar casos de prueba void test() { int res = isEulerian(); if (res == 0) System.out.println('graph is not Eulerian'); out.println('el gráfico tiene una ruta de Euler'); else System.out.println('el gráfico tiene un ciclo de Euler'); // Método del controlador public static void main(String args[]) { / / Creemos y probemos los gráficos que se muestran en las figuras anteriores Graph g1 = new Graph(5); g1.addEdge(1, 0); (0, 3); g1.addEdge(3, 4); g1.test(); Gráfico g2 = nuevo Gráfico(5); addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); g2.test(); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.prueba(); // Creemos un gráfico con 3 vértices // conectados en forma de ciclo Gráfico g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.prueba(); // Creemos un gráfico con todos los vértices // con grado cero Graph g5 = new Graph(3); g5.prueba(); } } // Este código es una contribución de Aakash Hasija> |
>
>
Python3
hacer y mientras bucle en java
# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections>import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> >def> __init__(>self>, vertices):> >self>.V>=> vertices># No. of vertices> >self>.graph>=> defaultdict(>list>)># default dictionary to store graph> ># function to add an edge to graph> >def> addEdge(>self>, u, v):> >self>.graph[u].append(v)> >self>.graph[v].append(u)> ># A function used by isConnected> >def> DFSUtil(>self>, v, visited):> ># Mark the current node as visited> >visited[v]>=> True> ># Recur for all the vertices adjacent to this vertex> >for> i>in> self>.graph[v]:> >if> visited[i]>=>=> False>:> >self>.DFSUtil(i, visited)> >'''Method to check if all non-zero degree vertices are> >connected. It mainly does DFS traversal starting from> >node with non-zero degree'''> >def> isConnected(>self>):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.V)> ># Find a vertex with non-zero degree> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i]) !>=> 0>:> >break> ># If there are no edges in the graph, return true> >if> i>=>=> self>.V>->1>:> >return> True> ># Start DFS traversal from a vertex with non-zero degree> >self>.DFSUtil(i, visited)> ># Check if all non-zero degree vertices are visited> >for> i>in> range>(>self>.V):> >if> visited[i]>=>=> False> and> len>(>self>.graph[i])>>0>:> >return> False> >return> True> >'''The function returns one of the following values> >0 -->Si la gráfica no es euleriana> >1 -->Si el gráfico tiene un camino de Euler (Semi-Eulerian)> >2 -->Si el gráfico tiene un circuito de Euler (euleriano) '''> >def> isEulerian(>self>):> ># Check if all non-zero degree vertices are connected> >if> self>.isConnected()>=>=> False>:> >return> 0> >else>:> ># Count vertices with odd degree> >odd>=> 0> >for> i>in> range>(>self>.V):> >if> len>(>self>.graph[i])>%> 2> !>=> 0>:> >odd>+>=> 1> >'''If odd count is 2, then semi-eulerian.> >If odd count is 0, then eulerian> >If count is more than 2, then graph is not Eulerian> >Note that odd count can never be 1 for undirected graph'''> >if> odd>=>=> 0>:> >return> 2> >elif> odd>=>=> 2>:> >return> 1> >elif> odd>>2>:> >return> 0> ># Function to run test cases> >def> test(>self>):> >res>=> self>.isEulerian()> >if> res>=>=> 0>:> >print>(>'graph is not Eulerian'>)> >elif> res>=>=> 1>:> >print>(>'graph has a Euler path'>)> >else>:> >print>(>'graph has a Euler cycle'>)> # Let us create and test graphs shown in above figures> g1>=> Graph(>5>)> g1.addEdge(>1>,>0>)> g1.addEdge(>0>,>2>)> g1.addEdge(>2>,>1>)> g1.addEdge(>0>,>3>)> g1.addEdge(>3>,>4>)> g1.test()> g2>=> Graph(>5>)> g2.addEdge(>1>,>0>)> g2.addEdge(>0>,>2>)> g2.addEdge(>2>,>1>)> g2.addEdge(>0>,>3>)> g2.addEdge(>3>,>4>)> g2.addEdge(>4>,>0>)> g2.test()> g3>=> Graph(>5>)> g3.addEdge(>1>,>0>)> g3.addEdge(>0>,>2>)> g3.addEdge(>2>,>1>)> g3.addEdge(>0>,>3>)> g3.addEdge(>3>,>4>)> g3.addEdge(>1>,>3>)> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4>=> Graph(>3>)> g4.addEdge(>0>,>1>)> g4.addEdge(>1>,>2>)> g4.addEdge(>2>,>0>)> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5>=> Graph(>3>)> g5.test()> # This code is contributed by Neelam Yadav> |
>
>
C#
dhl significa qué
// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> >private> int> V;>// No. of vertices> > >// Array of lists for Adjacency List Representation> >private> List<>int>>[]adj;> > >// Constructor> >Graph(>int> v)> >{> >V = v;> >adj =>new> List<>int>>[en];> >for> (>int> i=0; i adj[i] = new List |
>
>
JavaScript
> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> >// Constructor> >constructor(v)> >{> >this>.V = v;> >this>.adj =>new> Array(v);> >for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i |
>
>
cómo recuperar aplicaciones ocultasProducción
graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle>
Complejidad del tiempo: O(V+E)
Complejidad espacial: O(V+E)
Siguientes artículos:
Camino Euleriano y circuito para grafos dirigidos.
¿Algoritmo de Fleury para imprimir un camino o circuito euleriano?
