La clasificación por inserción y la clasificación por selección son dos algoritmos de clasificación populares y su principal diferencia radica en cómo seleccionan y colocan elementos en una secuencia ordenada.
Orden de selección:
- En la ordenación por selección, la matriz de entrada se divide en dos partes: una parte ordenada y una parte sin clasificar.
- El algoritmo encuentra repetidamente el elemento mínimo en la parte no ordenada y lo intercambia con el elemento más a la izquierda de la parte no ordenada, expandiendo así la parte ordenada en un elemento.
- La clasificación por selección tiene una complejidad temporal de O(n^2) en todos los casos.
Tipo de inserción:
- En la ordenación por inserción, la matriz de entrada también se divide en dos partes: una parte ordenada y una parte sin clasificar.
El algoritmo toma un elemento de la parte no ordenada y lo coloca en la posición correcta en la parte ordenada, desplazando los elementos más grandes una posición hacia la derecha.
La ordenación por inserción tiene una complejidad temporal de O(n^2) en el peor de los casos, pero puede funcionar mejor en matrices parcialmente ordenadas, con una complejidad temporal de O(n) en el mejor de los casos.
Principales diferencias: - La clasificación por selección escanea la parte no ordenada para encontrar el elemento mínimo, mientras que la clasificación por inserción escanea la parte ordenada para encontrar la posición correcta para colocar el elemento.
La ordenación por selección requiere menos intercambios que la ordenación por inserción, pero más comparaciones.
La ordenación por inserción es más eficiente que la ordenación por selección cuando la matriz de entrada está parcialmente o casi ordenada, mientras que la ordenación por selección funciona mejor cuando la matriz está muy desordenada.
En resumen, ambos algoritmos tienen una complejidad temporal similar, pero sus métodos de selección y colocación difieren. La elección entre ellos depende de las características de los datos de entrada y de los requisitos específicos del problema en cuestión.
Ventajas de la ordenación por inserción:
- Sencillo y fácil de entender e implementar.
- Eficiente para conjuntos de datos pequeños o datos casi ordenados.
- Algoritmo de clasificación local, lo que significa que no requiere memoria adicional.
- Algoritmo de clasificación estable, lo que significa que mantiene el orden relativo de elementos iguales en la matriz de entrada.
Desventajas de la ordenación por inserción:
- Ineficiente para grandes conjuntos de datos o datos ordenados de forma inversa, con una complejidad temporal en el peor de los casos de O(n^2).
- La ordenación por inserción tiene muchos intercambios, lo que puede hacer que sea lenta en las computadoras modernas.
Ventajas de la clasificación por selección:
- Sencillo y fácil de entender e implementar.
- Eficiente para conjuntos de datos pequeños o datos casi ordenados.
- Algoritmo de clasificación local, lo que significa que no requiere memoria adicional.
Desventajas de la clasificación por selección:
- Ineficiente para grandes conjuntos de datos, con una complejidad temporal en el peor de los casos de O(n^2).
- La clasificación de selección tiene muchas comparaciones, lo que puede hacer que sea lenta en las computadoras modernas.
- Algoritmo de clasificación inestable, lo que significa que puede no mantener el orden relativo de elementos iguales en la matriz de entrada.
En este artículo, analizaremos la diferencia entre el tipo de inserción y el tipo de selección:
Tipo de inserción es un algoritmo de clasificación simple que funciona de manera similar a la forma en que clasificas las cartas en tus manos. La matriz está prácticamente dividida en una parte ordenada y otra sin clasificar. Los valores de la parte sin clasificar se seleccionan y se colocan en la posición correcta en la parte ordenada.
Algoritmo:
Para ordenar una matriz de tamaño n en orden ascendente:
- Itere desde arr[1] hasta arr[n] sobre la matriz.
- Compare el elemento actual (clave) con su predecesor.
- Si el elemento clave es más pequeño que su predecesor, compárelo con los elementos anteriores. Mueva los elementos más grandes una posición hacia arriba para dejar espacio para el elemento intercambiado.
A continuación se muestra la imagen para ilustrar la clasificación por inserción:
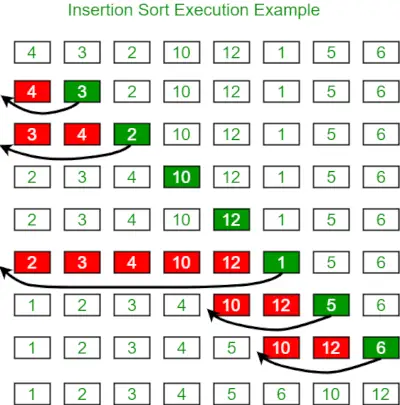
A continuación se muestra el programa para el mismo:
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arreglo[j]> clave) { arreglo[j + 1] = arreglo[j]; j = j - 1; } arr[j + 1] = clave; } } // Función para imprimir una matriz de tamaño N void printArray(int arr[], int n) { int i; // Imprime la matriz para (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arreglo[j]> clave) { arreglo[j + 1] = arreglo[j]; j = j - 1; } arr[j + 1] = clave; } } // Función para imprimir una matriz de tamaño N static void printArray(int arr[], int n) { int i; // Imprime la matriz para (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Código del controlador public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; int N = arr.length; // Llamada a función insertionSort(arr, N); Este código es aportado por code_hunt> |
>
>
Python3
# Python 3 program for the insertion sort> # Function to sort an array using> # insertion sort> def> insertionSort(arr, n):> >i>=> 0> >key>=> 0> >j>=> 0> >for> i>in> range>(>1>,n,>1>):> >key>=> arr[i]> >j>=> i>-> 1> ># Move elements of arr[0..i-1],> ># that are greater than key to> ># one position ahead of their> ># current position> >while> (j>>=> 0> and> arr[j]>clave):> >arr[j>+> 1>]>=> arr[j]> >j>=> j>-> 1> >arr[j>+> 1>]>=> key> # Function to print an array of size N> def> printArray(arr, n):> >i>=> 0> ># Print the array> >for> i>in> range>(n):> >print>(arr[i],end>=> ' '>)> >print>(>'
'>,end>=> '')> # Driver Code> if> __name__>=>=> '__main__'>:> >arr>=> [>12>,>11>,>13>,>5>,>6>]> >N>=> len>(arr)> ># Function Call> >insertionSort(arr, N)> >printArray(arr, N)> > ># This code is contributed by bgangwar59.> |
>
>
C#
// C# program for the above approach> using> System;> class> GFG> {> >// Function to sort an array using> >// insertion sort> >static> void> insertionSort(>int>[] arr,>int> n)> >{> >int> i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arreglo[j]> clave) { arreglo[j + 1] = arreglo[j]; j = j - 1; } arr[j + 1] = clave; } } // Función para imprimir una matriz de tamaño N static void printArray(int[] arr, int n) { int i; // Imprime la matriz para (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Código del controlador static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Length; // Llamada a función insertionSort(arr, N); printArray(arr, N); contribuido por Dharanendra L V> |
>
>
JavaScript
> // JavaScript program for the above approach> // Function to sort an array using> // insertion sort> function> insertionSort(arr,n)> {> >let i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arreglo[j]> clave) { arreglo[j + 1] = arreglo[j]; j = j - 1; } arr[j + 1] = clave; } } // Función para imprimir una matriz de tamaño N function printArray(arr,n) { let i; // Imprime la matriz para (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Código del controlador let arr=[12, 11 , 13, 5, 6]; let N = arr.length; // Llamada a función insertionSort(arr, N); printArray(arr, N); // Este código es una contribución de avanitrachhadiya2155> |
>
>Producción:
5 6 11 12 13>
El clasificación de selección El algoritmo ordena una matriz encontrando repetidamente el elemento mínimo (considerando el orden ascendente) de la parte no ordenada y colocándolo al principio. El algoritmo mantiene dos subarreglos en una matriz determinada.
- El subarreglo ya está ordenado.
- El subconjunto restante no está ordenado.
En cada iteración de la clasificación por selección, el elemento mínimo (considerando el orden ascendente) del subarreglo sin clasificar se selecciona y se mueve al subarreglo ordenado.
A continuación se muestra un ejemplo que explica los pasos anteriores:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>
A continuación se muestra el programa para el mismo:
C++
// C++ program for implementation of> // selection sort> #include> using> namespace> std;> // Function to swap two number> void> swap(>int>* xp,>int>* yp)> {> >int> temp = *xp;> >*xp = *yp;> >*yp = temp;> }> // Function to implement the selection> // sort> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array:
'; // Print the array printArray(arr, n); return 0; }> |
>
>
Java
// Java program for implementation of> // selection sort> import> java.util.*;> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995> |
>
>
Python3
# Python3 program for implementation of> # selection sort> # Function to implement the selection> # sort> def> selectionSort(arr, n):> ># One by one move boundary of> ># unsorted subarray> >for> i>in> range>(n>-> 1>):> ># Find the minimum element> ># in unsorted array> >min_idx>=> i> >for> j>in> range>(i>+> 1>, n):> >if> (arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp> |
>
>
C#
escáner.siguiente java
// C# program for implementation of> // selection sort> using> System;> public> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> []arr,>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array:
'); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1> |
>
>
JavaScript
> // Javascript program for implementation of> // selection sort> // Function to implement the selection> // sort> function> selectionSort(arr, n)> {> >let i, j, min_idx;> > >// One by one move boundary of> >// unsorted subarray> >for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127> |
>
>Producción:
Sorted array: 11 12 22 25 64>
Diferencia tabular entre ordenación por inserción y ordenación por selección:
| Tipo de inserción | Orden de selección | |
|---|---|---|
| 1. | Inserta el valor en la matriz preordenada para ordenar el conjunto de valores en la matriz. | Encuentra el número mínimo/máximo de la lista y lo ordena en orden ascendente/descendente. |
| 2. | Es un algoritmo de clasificación estable. | Es un algoritmo de clasificación inestable. |
| 3. | La complejidad temporal en el mejor de los casos es Ω(N) cuando la matriz ya está en orden ascendente. Tiene Θ(N2) en el peor de los casos y en el caso medio. | Para el mejor de los casos, el peor de los casos y la clasificación de selección promedio tienen complejidad Θ(N2). |
| 4. | El número de operaciones de comparación realizadas en este algoritmo de clasificación es menor que el intercambio realizado. | El número de operaciones de comparación realizadas en este algoritmo de clasificación es mayor que el intercambio realizado. |
| 5. | Es más eficiente que el tipo Selección. | Es menos eficiente que el tipo de inserción. |
| 6. | Aquí se conoce de antemano el elemento y buscamos la posición correcta para colocarlos. | La ubicación donde poner el elemento se conoce previamente buscamos el elemento a insertar en esa posición. |
| 7. | La ordenación por inserción se utiliza cuando:
| La clasificación por selección se utiliza cuando
|
| 8. | La ordenación por inserción es adaptativa, es decir, eficiente para conjuntos de datos que ya están sustancialmente ordenados: la complejidad temporal es O(kn) cuando cada elemento en la entrada no es más que k lugares alejados de su posición ordenada | La clasificación por selección es un algoritmo de clasificación por comparación in situ |
