- DFA se refiere a autómatas finitos deterministas. Determinista se refiere a la unicidad del cálculo. Los autómatas finitos se denominan autómatas finitos deterministas si a la máquina lee una cadena de entrada, un símbolo a la vez.
- En DFA, solo hay una ruta para entradas específicas desde el estado actual al siguiente.
- DFA no acepta el movimiento nulo, es decir, DFA no puede cambiar de estado sin ningún carácter de entrada.
- DFA puede contener varios estados finales. Se utiliza en análisis léxico en el compilador.
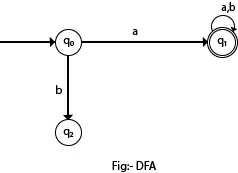
En el siguiente diagrama, podemos ver que desde el estado q0 para la entrada a, solo hay un camino que va a q1. De manera similar, desde q0, solo hay una ruta para que la entrada b vaya a q2.
Definición formal de DFA
Un DFA es una colección de 5 tuplas igual a la que describimos en la definición de FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
La función de transición se puede definir como:
δ: Q x ∑→Q
Representación gráfica de DFA
Un DFA se puede representar mediante dígrafos llamados diagrama de estado. En el cual:
- El estado está representado por vértices.
- El arco etiquetado con un carácter de entrada muestra las transiciones.
- El estado inicial está marcado con una flecha.
- El estado final se indica con un doble círculo.
Ejemplo 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Solución:
Diagrama de transición:

Tabla de transición:
| Estado actual | Siguiente estado para la entrada 0 | Siguiente estado de la entrada 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Ejemplo 2:
DFA con ∑ = {0, 1} acepta todos los que comienzan con 0.
Solución:

Explicación:
- En el diagrama anterior, podemos ver que, dado 0 como entrada a DFA en el estado q0, DFA cambia de estado a q1 y siempre va al estado final q1 al iniciar la entrada 0. Puede aceptar 00, 01, 000, 001... .etc. No puede aceptar ninguna cadena que comience con 1, porque nunca llegará al estado final en una cadena que comience con 1.
Ejemplo 3:
DFA con ∑ = {0, 1} acepta todos los que terminan en 0.
Solución:

Explicación:
En el diagrama anterior, podemos ver que dado 0 como entrada a DFA en el estado q0, el DFA cambia de estado a q1. Puede aceptar cualquier cadena que termine en 0, como 00, 10, 110, 100... etc. No puede aceptar ninguna cadena que termine en 1, porque nunca irá al estado final q1 en 1 entrada, por lo que la cadena que termine en 1 no será aceptada o será rechazada.
