Eliminar un nodo de un árbol AVL es similar a hacerlo en un árbol de búsqueda binario. La eliminación puede alterar el factor de equilibrio de un árbol AVL y, por lo tanto, es necesario reequilibrar el árbol para mantener la AVL. Para ello necesitamos realizar rotaciones. Los dos tipos de rotaciones son rotación L y rotación R. Aquí, discutiremos las rotaciones R. Las rotaciones L son imágenes especulares de ellas.
Si el nodo que se va a eliminar está presente en el subárbol izquierdo del nodo crítico, entonces se debe aplicar la rotación L; de lo contrario, el nodo que se va a eliminar está presente en el subárbol derecho del nodo crítico. , se aplicará la rotación R.
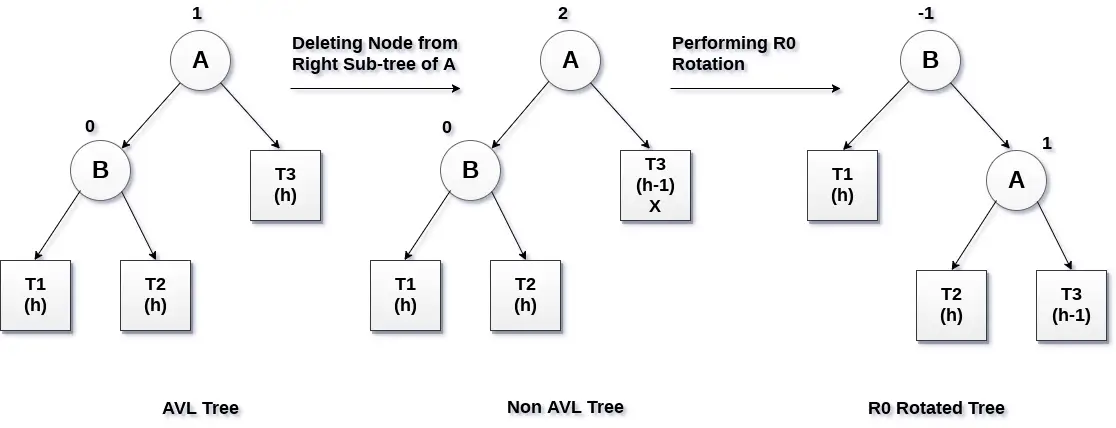
Consideremos que A es el nodo crítico y B es el nodo raíz de su subárbol izquierdo. Si se desea eliminar el nodo X, presente en el subárbol derecho de A, pueden darse tres situaciones diferentes:
Rotación R0 (el nodo B tiene factor de equilibrio 0)
Si el nodo B tiene un factor de equilibrio 0 y el factor de equilibrio del nodo A se altera al eliminar el nodo X, entonces el árbol se reequilibrará rotando el árbol usando la rotación R0.
El nodo crítico A se mueve hacia su derecha y el nodo B se convierte en la raíz del árbol con T1 como subárbol izquierdo. Los subárboles T2 y T3 se convierten en los subárboles izquierdo y derecho del nodo A. El proceso involucrado en la rotación R0 se muestra en la siguiente imagen.
Ejemplo:
Elimine el nodo 30 del árbol AVL que se muestra en la siguiente imagen.

Solución
En este caso, el nodo B tiene un factor de equilibrio 0, por lo tanto, el árbol se rotará utilizando la rotación R0 como se muestra en la siguiente imagen. El nodo B(10) se convierte en la raíz, mientras que el nodo A se mueve hacia su derecha. El hijo derecho del nodo B ahora se convertirá en el hijo izquierdo del nodo A.
numeros romanos del 1 al 100

Rotación R1 (el nodo B tiene factor de equilibrio 1)
La rotación R1 se realizará si el factor de equilibrio del nodo B es 1. En la rotación R1, el nodo crítico A se mueve hacia su derecha teniendo los subárboles T2 y T3 como sus hijos izquierdo y derecho respectivamente. T1 se colocará como el subárbol izquierdo del nodo B.
El proceso involucrado en la rotación de R1 se muestra en la siguiente imagen.

Ejemplo
Elimine el nodo 55 del árbol AVL que se muestra en la siguiente imagen.

Solución :
Eliminar 55 del árbol AVL altera el factor de equilibrio del nodo 50, es decir, el nodo A, que se convierte en el nodo crítico. Esta es la condición de la rotación R1 en la que el nodo A se moverá hacia su derecha (como se muestra en la imagen a continuación). La derecha de B ahora se convierte en la izquierda de A (es decir, 45).
El proceso involucrado en la solución se muestra en la siguiente imagen.

Rotación R-1 (El nodo B tiene factor de equilibrio -1)
La rotación R-1 se realizará si el nodo B tiene un factor de equilibrio -1. Este caso se trata de la misma manera que la rotación LR. En este caso, el nodo C, que es el hijo derecho del nodo B, se convierte en el nodo raíz del árbol con B y A como hijos izquierdo y derecho respectivamente.
Los subárboles T1, T2 se convierten en los subárboles izquierdo y derecho de B, mientras que T3, T4 se convierten en los subárboles izquierdo y derecho de A.
El proceso involucrado en la rotación de R-1 se muestra en la siguiente imagen.

Ejemplo
Elimine el nodo 60 del árbol AVL que se muestra en la siguiente imagen.
javascript al hacer clic

Solución:
en este caso, el nodo B tiene un factor de equilibrio -1. La eliminación del nodo 60 altera el factor de equilibrio del nodo 50, por lo que es necesario girarlo R-1. El nodo C, es decir, 45, se convierte en la raíz del árbol con el nodo B(40) y A(50) como sus hijos izquierdo y derecho.

